分数阶系统的二自由度PID预期动态整定法
李明大,王 京,李东海
(1.北京科技大学冶金工程研究院,北京,100083;2.清华大学热能工程系,北京,100084)
分数阶微积分将微分、积分的阶次扩展到实数范围,拓展了人们所熟知的整数阶微积分的描述能力。计算机仿真软件的快速发展使得越来越多的学者将分数阶微积分算法用于控制器的设计。分数阶控制最早应用于CRONE控制器[1]。随后,Podlubny等将分数阶PID控制器(FO-PID)引入分数阶系统的控制中,取得了良好的效果[2-4]。针对分数阶模型,文献[5]提出了一种基于幅相裕度的分数阶PID整定方法。此外遗传算法、根轨迹法等也被用于分数阶PID的参数选取[6-7]。文献[8-9]详细讨论了分数阶PID控制器积分与微分的阶次变化对控制系统的影响。对于两类分数阶模型,文献[10]与文献[11]分别设计了形如(Kp+Ki/s)λ的分数阶[PI]控制器(FO-[PI])和形如Kp(1+Kds)μ的分数阶[PD]控制器(FO-[PD]),仿真结果表明分数阶[PI]、[PD]控制器要优于分数阶PI、PD控制器。
分数阶微积分能更加准确地描述自然物理现象,但在控制器中分数阶特性的实现却不容易。例如,单一的分数阶算子要用高阶传递函数或有限时间截断来近似,在离散系统中也要用高阶的离散传递函数来近似[10-13]。然而在很多生产过程中,如高速中厚板轧制,对控制器和控制算法的快速性要求非常高[14-16],因此,针对更真实的分数阶模型,设计出简单易整定的控制器是很必要的。文献[17]研究了一种非线性鲁棒控制器,将控制器参数与系统预期动态相结合,使得控制器参数具有实际物理意义,而文献[18]将此方法与PID控制器相结合,针对常见的工业对象提出了基于预期动态的PID整定方法。文献[19]研究了分数阶系统的自抗扰控制,将分数阶动态当作系统扰动进行实时估计并予以抵消。在上述研究基础上,本文采用二自由度PID控制器,针对分数阶模型提出基于预期动态方程的简单整定方法——DDE法,通过仿真对DDE法的有效性进行验证,并与其他分数阶控制方法的控制效果进行比较。
1 分数阶系统简介
描述分数阶控制系统最常见的数学定义是Grünwald-Letnikov分数阶微分定义式:
(1)
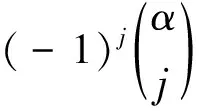
在零初始状态下,分数阶微分的拉普拉斯变换为
L [Dαf(t)]=sαF(s)
(2)
考虑单入单出时不变分数阶系统,其传递函数有如下形式:
(3)
式中:q>0,n>0,m≥0,均为整数,且n>m;H为系统高频增益,H≠0;ai(i=0,1,…,n-1)、bi(i=0,1,…,m-1)为未知系数。令r=n-m/q,r为系统的相对阶。
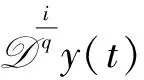
(4)
得到系统的标准型:
(5)
式中:ci(i=0,1,…,n-m)、di(i=0,1,…,m-1)为未知系数;u为控制输入。
2 预期动态法
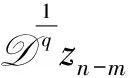
(6)
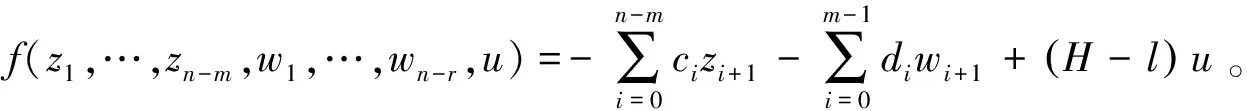
在满足假设②的条件下,如果f可测,则系统(5)的控制律可化为
(7)
其保证了闭环系统(5)和式(7)的特征值分别与多项式h0+h1s+…+hn-m-1sn-m-1+sn-m以及B(s)相一致。
由于所有状态不可测并且系数ci、di与H都未知,控制律(7)是不可实现的。在此引入积分器来抵消f的影响,故控制律可重新写为
(8)
式中:
(9)
(10)
且hii=0,…,n-m-1为适当的正常数。
当n-m=2时,闭环系统的预期动态方程为
(11)
其所对应的控制律为
(12)
将式(6)与式(9)代入式(10)中,遵循简单控制原则可得到:
(13)
为快速跟踪f并达到适当的稳定裕度,取k=10。因此式(12)可化为
u=-h0(y-r)-h1sy-
(14)
化简可得到二自由度PID控制律:
(15)
式中:
(16)
二自由度PID结构如图1所示,其中虚框所指由DDE法整定。
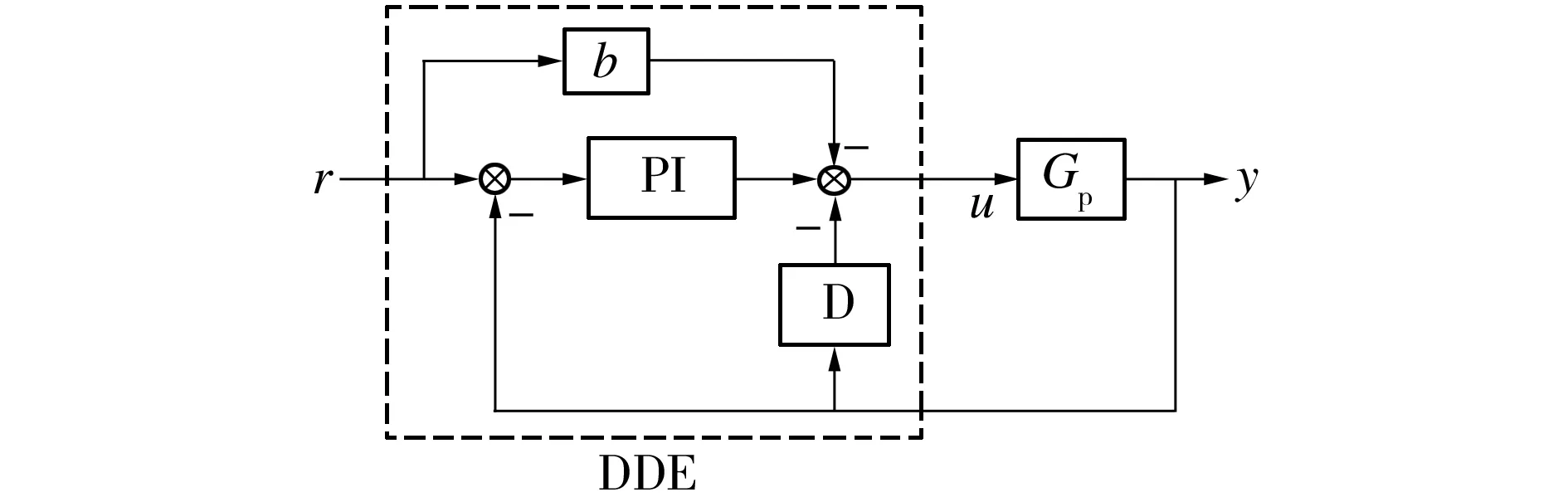
图1 二自由度PID结构形式Fig.1 2-DOF PID structure
式(16)中各参数的选取规则如下:
(1)根据控制要求确定预期动力学方程(11)的系数。设定调节时间TS,超调量要尽量小。根据经典控制理论对二阶系统的分析,并考虑到实际动态性能与预期动态存在偏差,需要保证足够的性能裕度,故取:
(17)
式中:T=TS/6。
(2)调整单一参数l。令l值从接近0的一个很小的值(如0.0001)开始单调增加。当系统超调量在0~1%之间变化时,固定此l值为控制器参数。
(3)按式(16)计算二自由度PID控制器其他参数。通过仿真实验检验系统性能,满足要求则整定结束,否则可能是因为TS设定得太小,需返回(1)重新设计。
3 分数阶模型控制仿真
3.1 分数阶模型及其控制参数
为了验证DDE法的有效性,笔者从文献中选取8个主要的分数阶模型(1个加热炉模型和7个虚拟的分数阶模型)进行对比仿真分析,如表1所示,其中模型1为加热炉模型。文献[5]~文献[11]分别采用分数阶PID、[PI]和[PD]控制器对8个模型进行控制,控制器参数如表2所示。本文采用DDE方法设计了整数阶二自由度PID控制器(DDE-PID)对8个分数阶模型进行控制,控制器参数如表3所示。

表1 分数阶模型
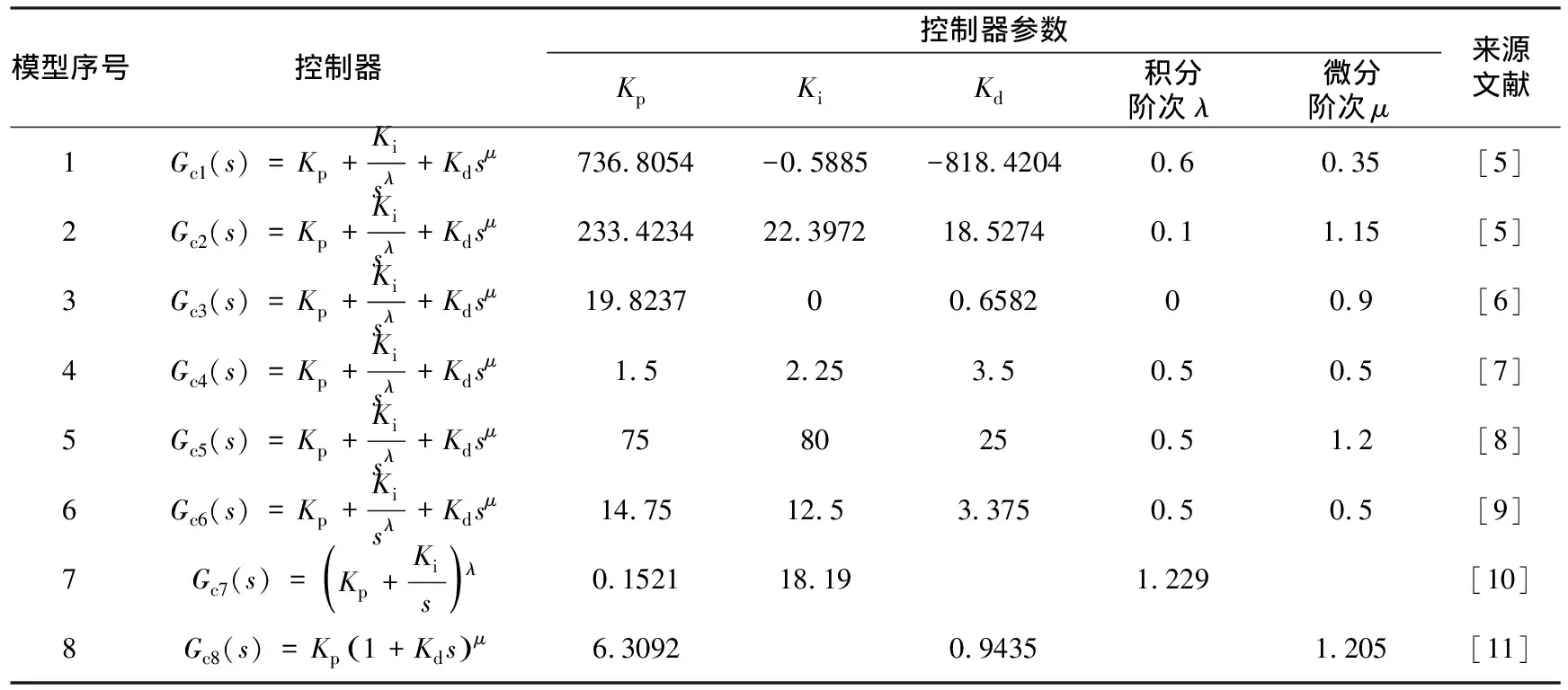
表2 分数阶控制器参数
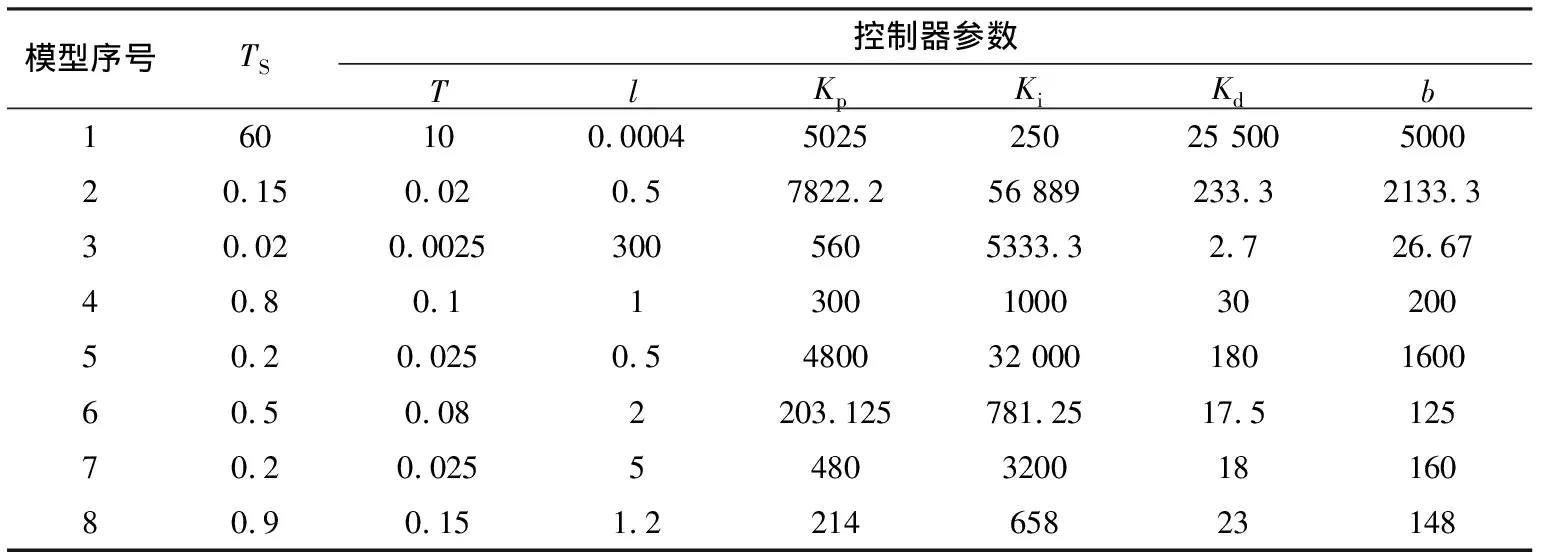
表3 DDE法整定的二自由度PID控制器参数
3.2 仿真结果与分析
文献[4]在建立加热炉的分数阶模型(简称FOM,即模型1)的同时也建立了其整数阶模型(简称IOM),如式(18)所示:
(18)
由图2可见,在控制更为精确的分数阶模型时,无论是分数阶PID控制器还是整数阶PID控制器均可达到较好的控制效果,并且本文设计的DDE-PID控制效果更好。
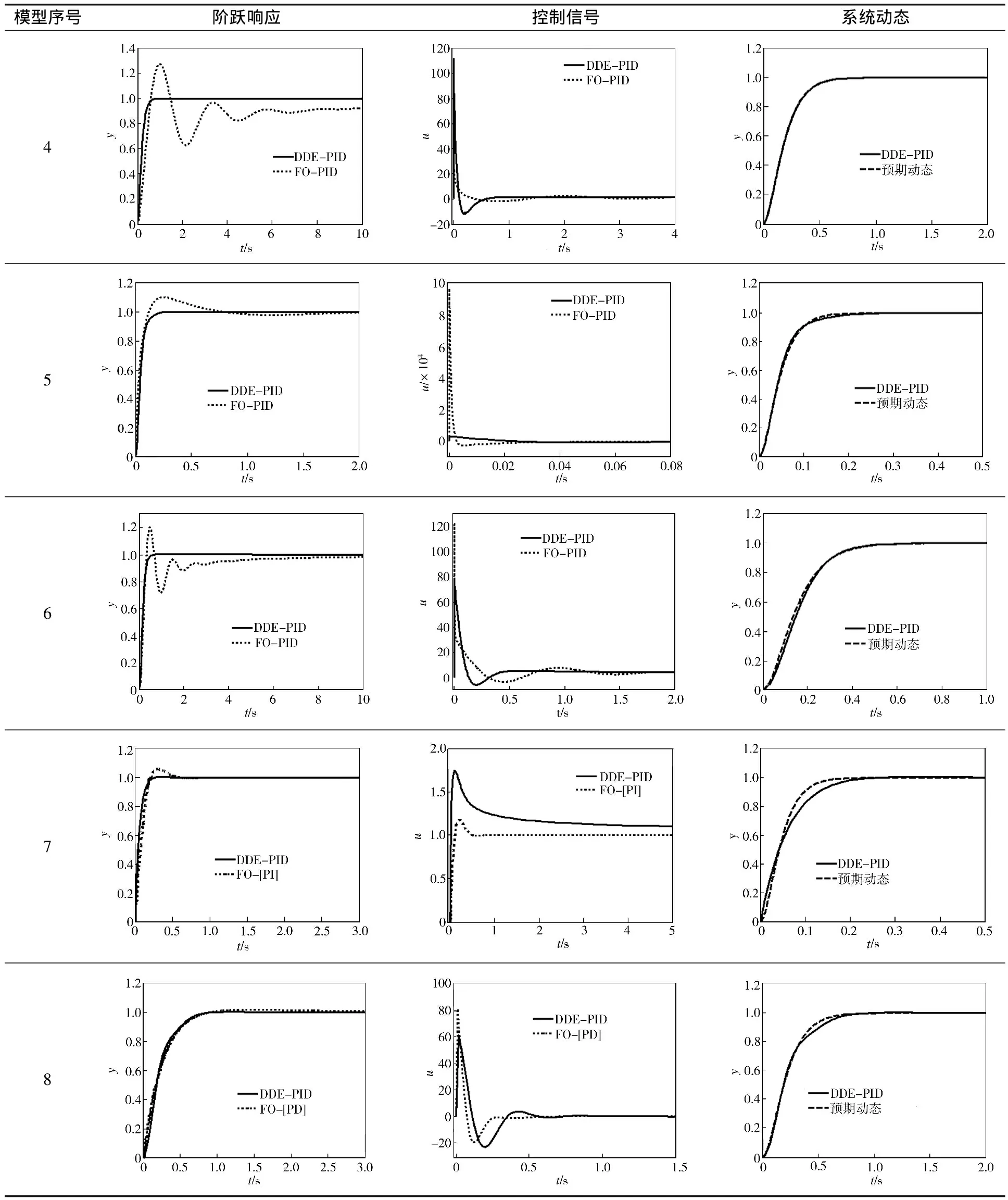
8个分数阶模型的控制仿真结果如表4所示,控制性能指标如表5所示。由表4和表5可见,分数阶PID和DDE-PID都能很好地控制分数阶模型,但DDE-PID控制的超调量更小,调节时间更短。同时,两种方法的控制信号处在同一数量级,甚至DDE-PID的控制代价更小一些。值得注意的是,DDE-PID控制可使系统的动态响应满足预期,其调节时间小于预期调节时间。另外,虽然FO-[PI]、FO-[PD]控制器比FO-PID控制器的效果更好,但DDE-PID也可达到与FO-[PI]和FO-[PD]相同的控制效果。
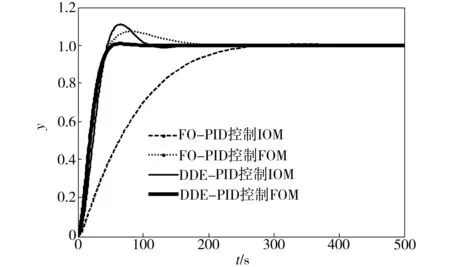
图2 FO-PID和DDE-PID对加热炉模型的控制效果比较
Fig.2StepresponsecomparisonofFOMandIOMcontrolledbyFO-PIDorDDE-PID
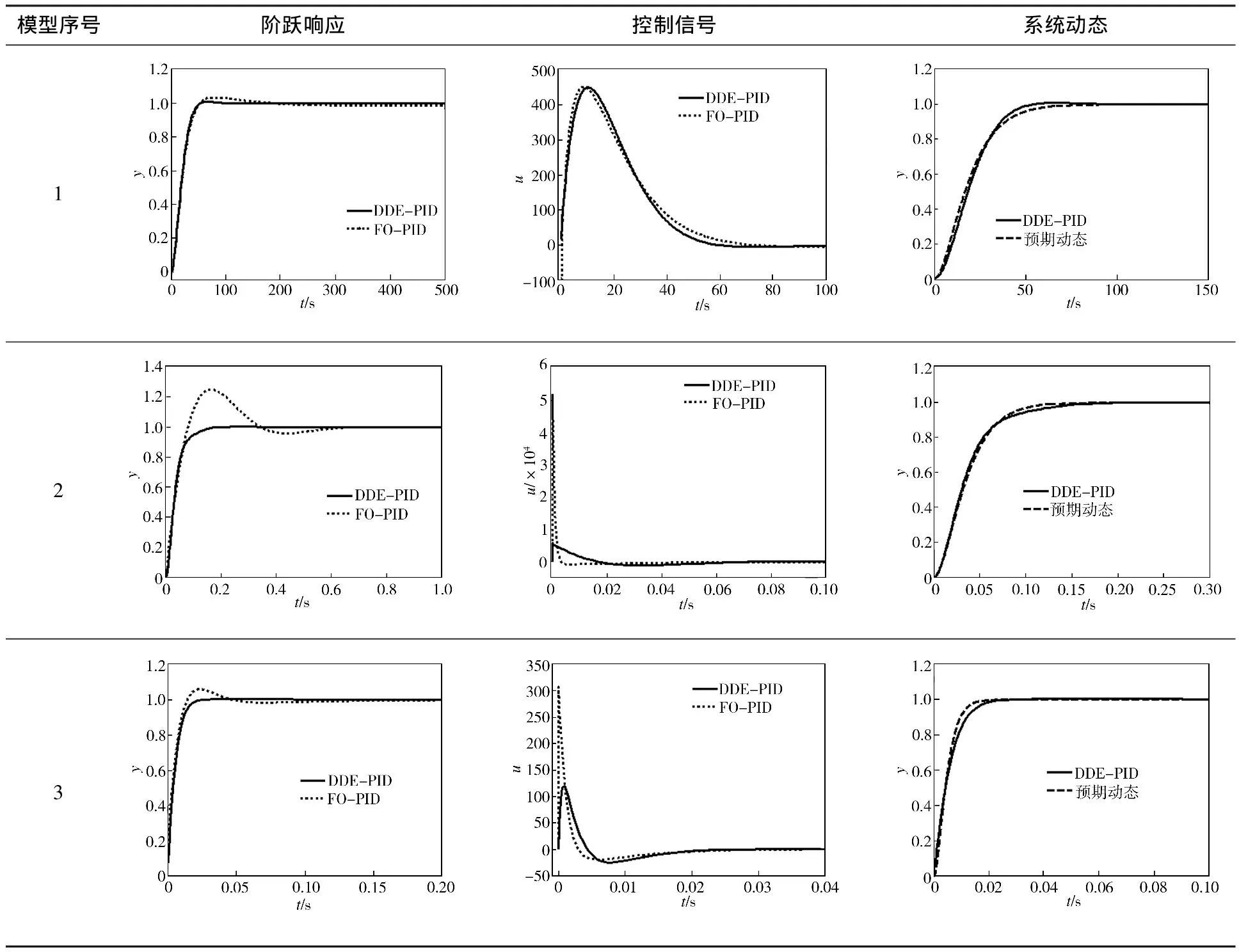
表4 分数阶模型的控制仿真结果
续表4
45678
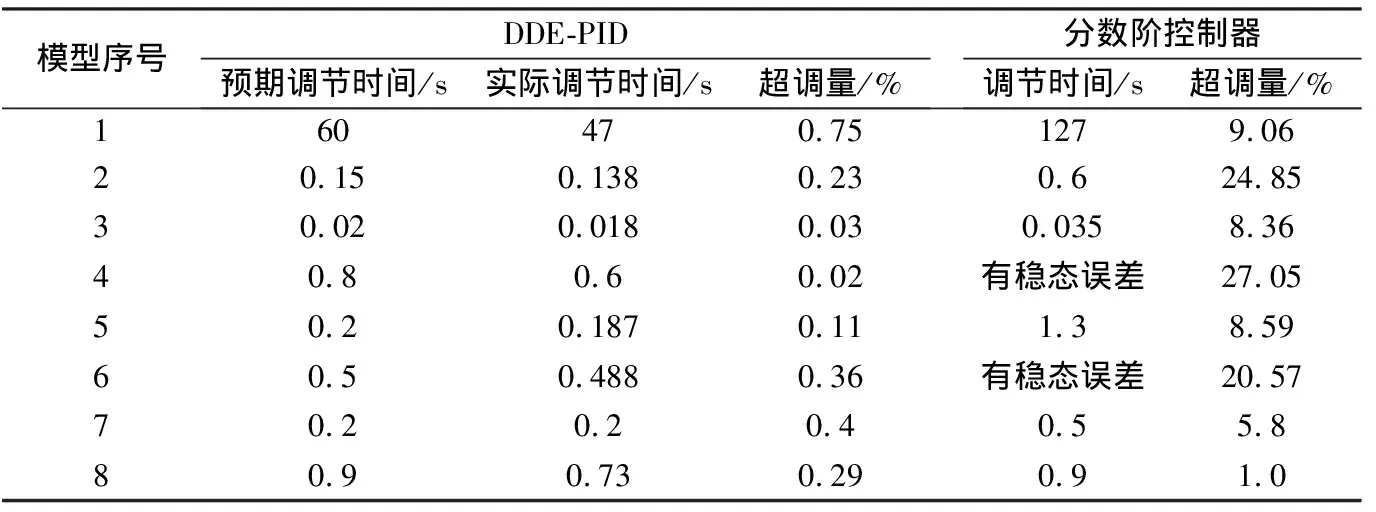
表5 控制性能指标比较
4 结语
本文采用实际模型简单控制的策略,针对一类分数阶模型提出一种基于预期动态方程的二自由度PID整定方法(DDE)。1个加热炉模型及7个虚拟分数阶模型的仿真实例验证了该方法的有效性。DDE-PID控制可使分数阶系统满足预期动态,并且在控制代价较小或相近的条件下可获得与分数阶PID相当或较其更好的控制效果。
与分数阶控制器不同,基于预期动态方程的二自由度PID整定方法不需要对现有的经典PID类型控制器进行大的改动,并且具有结构简单、整定方便等特点,因此DDE-PID的工业应用前景更为广阔。
[1] Oustaloup A.CRONE control:principle,synthesis,performances with nonlinearities and robustness-input immunity dilemma[J]. Lecture Notes in Control and Information Sciences, 1990, 144: 767-777.
[2] Podlubny I. Fractional-order systems and PIλDμcontrollers[J]. IEEE Transactions on Automatic Control, 1999, 44(1): 208-214.
[3] Podlubny I. Fractional differential equations[M]. San Diego: Academic Press, 1999.
[4] Podlubny I, Dorcak L, Kostial I. On fractional derivatives, fractional-order dynamic system and PIλDμcontrollers[C]//Proceedings of the 36th IEEE Conference on Decision and Control. San Diego, California, 1997: 4985-4990.
[5] Zhao Chunna, Xue Dingyu, Chen Yangquan. A fractional order PID tuning algorithm for a class of fractional order plants[C]∥Proceedings of the IEEE International Conference on Mechatronics and Automation. Niagara Falls, Canada, 2005: 216-221.
[6] 李大字,刘展,靳其兵,等. 基于遗传算法的分数阶控制器参数整定研究[J]. 控制工程, 2006, 13(4): 384-387.
[7] 曾庆山,曹广益,王振滨. 分数阶PIλDμ控制器的仿真研究[J]. 系统仿真学报, 2004, 16(3): 465-469.
[8] 曹娇.分数阶控制系统与新型控制器设计[D].北京:北京化工大学, 2008.
[9] Zeng Qingshan, Cao Guangyi, Zhu Xinjian. The effect of the fractional-order controller’s orders variation on the factional-order control systems[C]//Proceedings of the First International Conference on Machine Learning and Cybernetics. Beijing, China, 2002: 367-372.
[10]Luo Ying, Chen Yangquan, Wang Chunyang, et al. Tuning fractional order proportional integral controllers for fractional order systems[J]. Journal of Process Control, 2010, 20(7): 823-831.
[11]Luo Ying, Chen Yangquan. Fractional order [proportional derivative] controller for a class of fractional order systems[J]. Automatica, 2009, 45(10): 2446-2450.
[12]Oustaloup A, Levron F, Mathieu B, et al. Frequency-band complex noninteger differentiator: characterization and synthesis[J]. IEEE Transactions on Circuits and Systems(I): Fundamental Theory and Applications, 2000, 47(1): 25-39.
[13]Xue Dingyu, Zhao Chunna, Chen Yangquan. A modified approximation method of fractional order system[C]//Proceedings of the IEEE International Conference on Mechatronics and Automation. Luoyang, China, 2006: 1043-1048.
[14]李静,翟海龙,叶利峰,等. 基于自抗扰控制的秒流量AGC研究[J]. 武汉科技大学学报, 2013, 36(2): 88-93.
[15]叶利峰,王京,张飞. 基于模型补偿的自抗扰控制器研究[J]. 武汉科技大学学报, 2013, 36(2): 140-145.
[16]Wang Zhe, Li Jing, Wang Jing, et al. Active disturbance rejection control for electro-hydraulic servo system of aluminum strip cold rolling mill[C]//Proceedings of the 32nd Chinese Control Conference. Xi’an, China, 2013:974-979.
[17]Tornambe A, Valigi P. A decentralized controller for the robust stabilization of a class of MIMO dynamical systems[J]. Journal of Dynamic Systems, Measurement and Control, 1994, 116(2): 293-304.
[18]王维杰,李东海,高琪瑞,等. 一种二自由度PID控制器参数整定方法[J]. 清华大学学报:自然科学版, 2008, 48(11): 1962-1966.
[19]Li Mingda, Li Donghai, Wang Jing, et al. Active disturbance rejection control for fractional-order system[J]. ISA Transactions, 2013, 52(3): 365-374.

