动力总成悬置软垫结构参数优化系统开发

王 庆, 杨啟梁, 孙 丽

(武汉科技大学汽车与交通工程学院,湖北 武汉,430081)

汽车动力总成悬置系统的性能对整车NVH特性的优劣起着重要作用，尤其是在发动机怠速工况下[1]。悬置系统的设计包括两个方面，即悬置软垫刚度参数的优化和悬置软垫结构设计。在悬置软垫刚度参数优化方面，一般采用动力学优化方法，通过建立动力总成系统的六自由度或十二自由度动力学模型，以悬置系统解耦度或者悬置传递率、悬置支反力等为目标函数来优化悬置软垫刚度[2]。但是，在悬置软垫结构设计方面，到目前为止还没有一种快速、有效的设计方法。悬置软垫为橡胶材料，由于橡胶材料的非线性弹性特性，使得在三向刚度约束的条件下优化悬置的结构变得非常困难。在早期的悬置软垫开发中，一般是根据经验，通过不断改变其几何形状及参数进行反复试验来达到所需的刚度要求，这种开发模式不仅成本高、效率低，而且误差较大，已很难满足现代汽车产品性能的要求。随着CAE技术的发展，出现了具备超弹性特性材料模型和体积近似不可压缩的大变形计算功能的有限元软件(如ABAQUS、MARC、ANSYS、ADINA等)，采用有限元方法，可以很方便地计算出悬置软垫的三向刚度，减少了产品试制的成本和时间[3]。在有限元分析中，通过不断修改悬置软垫的几何参数来满足所需的刚度要求，这一过程非常繁琐，有时也很难获得理想的刚度参数。赵建才等[4]提出了一种利用遗传算法和神经网络相结合的策略对橡胶悬置软垫的几何结构参数进行优化的方法，可以直接优化出满足刚度要求的悬置软垫结构参数，节约了计算时间，提高了设计精度，但这种方法须由人工进行若干具有不同设计参数的有限元分析，以得到结构设计参数与三个方向的刚度之间的对应关系，影响了工作效率。本文在文献[4]的基础上，采用软件集成的方法，以MATLAB为平台，集成有限元分析软件ABAQUS，尝试开发一套悬置软垫结构参数优化系统，以期根据所提出的三向刚度要求，快速、准确地确定悬置软垫的结构参数来提高悬置结构设计的效率。

1 结构参数优化系统基本组成

本研究开发的悬置软垫结构参数优化系统的原理如图1所示。该系统采用MATLAB软件作为控制平台，由4个部分组成：第一部分是ABAQUS有限元迭代计算，能够自动计算得到一批悬置软垫结构参数对应的各向刚度，作为初始数据；第二部分是神经网络映射优化函数，通过BP神经网络学习初始数据，得到悬置软垫任意结构参数与其各向刚度之间的非线性映射，构建橡胶软垫的刚度函数；第三部分是遗传算法优化参数，对目标函数进行全局寻优得到目标函数的全局最小值，即得到悬置软垫设计刚度与目标刚度之间误差最小的结构参数值；第四部分是误差分析，分析优化的结构参数对应的刚度与目标刚度间的误差。系统运行完毕后，输出悬置软垫的结构参数、三向刚度及刚度误差。

图1 悬置软垫结构参数优化系统原理图

2 悬置软垫刚度的有限元自动计算

要对橡胶软垫的各向刚度进行有限元计算，首先要确定橡胶材料的本构关系。对于各向同性、体积不可压缩或体积近似不可压缩的橡胶材料，其非线性弹性特性一般用超弹性本构模型来描述。目前较成熟的本构模型有基于连续介质力学理论的Mooney-Rivlin模型、Ogden模型和基于热力学统计理论的Arruda-Boyc模型，其中Mooney-Rivlin模型是一个应用最广泛的经典模型，可以模拟很多橡胶材料的力学行为。Mooney-Rivlin模型的应力-应变关系为[5]：

σ=2(λ-λ-2)(C01+C10λ-1)

(1)

式中：σ为应力；λ为应变；C01和C10为材料常数。

当采用该模型时，一般假设C01+C10为线性关系，从而材料的剪切模量G与材料常数的关系为G=2(C01+C10)。假定材料体积不可压缩，则杨氏模量E=6(C01+C10)。根据以上理论，在工程实践中可通过测量橡胶材料的邵氏硬度HA，将其转化成杨氏模量

(2)

并假定C01=0.25C10，从而求得C01和C10的值。

本系统用ABAQUS对橡胶软垫进行有限元计算，建立的分析模型包含6部分信息：几何形状、材料数据、载荷和边界条件、网格划分、分析类型和输出要求。对悬置软垫的几何形状进行一定的简化处理，简化的结构更方便在ABAQUS中建立模型，减少有限元分析中的计算量。划分网格是有限元模型的一个重要环节，它要求考虑的问题较多，工作量较大，所划分的网格形式由于划分者的水平和思路不同而有很大差异，因而对计算精度和计算规模会产生显著影响。为便于批处理运算，采用结构化网格技术(STRUCTURED)、中性轴算法(Medial Axis)、四面体(Tet)单元和杂交公式进行划分。

当需要多次进行不同参数的有限元计算时，ABAQUS/CAE每次都需要人工重新建模，对参数逐个分析，工作量非常大，影响效率。通过对ABAQUS内核Python语言的研究，发现ABAQUS内核程序包含了ABAQUS/CAE所有的对象数据和方法，可实现应用程序编程接口(API)来操作内核程序，使其独立于ABAQUS/GUI而在底层运行[6]。因此，本系统通过使用Python语言编写批处理子程序，能够让ABAQUS自动生成在一定范围内的结构设计参数所对应的三向刚度，其步骤如下：

(1)根据实际应用的悬置软垫的结构需要，确定结构参数及其范围。

(2)按照初始结构参数建立悬置模型，进行有限元分析。

(3)记录该有限元分析结果，按一定步长迭代结构参数。

在MATLAB中调用ABAQUS的批处理子程序，由ABAQUS自动进行有限元批处理计算并将计算结果直接返回MATLAB工作空间，再由MATLAB进行数据处理，最后得到悬置软垫不同结构参数所对应的三向刚度，该数据作为BP神经网络的初始训练数据。

3 建立神经网络优化函数

在悬置软垫的优化设计过程中，必须要有软垫刚度Ki与结构参数fi(t)之间的函数：

Ki=fi(t1，t2，…,tn) (i=x，y，z)

(3)

本系统采用BP神经网络来建立这种高度非线性的函数关系，称之为神经网络优化函数。利用MATLAB提供的神经网络工具箱(Neural Network Toolbox，简称NNbox)编写BP神经网络系统，建立三层BP网络，其中输入层各神经元负责接收并传递外部信息，即悬置软垫的结构参数；中间层负责信息处理和变换；输出层向外界输出信息处理结果，即悬置软垫的三向刚度。

使用ABAQUS批处理计算得到的初始数据训练BP神经网络，过程由正向传播和反向传播组成。正向传播过程中，ABAQUS迭代时所用的软垫结构参数集从输入层经中间层单元逐层处理，并传向输出层，每一层神经元的状态只影响下一层神经元的状态。如果在输出层得到的训练各向刚度集与ABAQUS计算得到各向刚度集的均方误差不小于0.01时，则转向反向传播，将输出的误差按原来的连接通路返回。在外界输入样本的刺激下不断改变网络的连接权值，以使网络的输出不断地接近期望的输出，得到合适的网络连接值后，便可对新样本进行非线性映像，即得到发动机悬置软垫的结构参数与各向刚度之间的映射关系。

4 遗传算法全局寻优

在得到悬置软垫三向刚度的神经网络优化函数后便可进行优化计算。首先是确定优化目标函数，要使悬置软垫的三向刚度均达到目标值，这是一个多目标优化问题，可以通过加权的方法将多目标函数转化成单一目标优化问题，构造目标函数g：

g=α1(Kx-Kmx)2+

α2(Ky-Kmy)2+α3(Kz-Kmz)2

(4)

式中：Kx、Ky、Kz分别为悬置软垫在x、y、z方向的刚度；Kmx、Kmy、Kmx分别为悬置软垫在x、y、z方向的目标刚度；α1、α2和α3为权重值，根据悬置软垫在三方向的刚度对隔振所起的作用而取值。

本系统采用遗传算法进行结构参数优化。利用英国谢菲尔德(Sheffield)大学推出的基于MATLAB的遗传算法工具箱，根据悬置软垫结构设计的需要编写遗传算法寻优程序。具体步骤如下：

(1)随机产生初始种群。

(2)编码。将悬置软垫结构参数按照二进制编码转换到遗传算法所能处理的搜索空间。

(3)确定适应度函数。根据目标函数g设定适应度值。

(4)进行选择、交叉和变异遗传操作，输出并保存结果。

5 悬置软垫结构参数优化计算实例

某动力总成前悬置结构软垫的结构简图如图2所示。该悬置软垫为环柱型结构，设计目标刚度为Kmx=Kmy= 50 N/mm，Kmz= 150 N/mm，材料为天然橡胶，邵氏硬度HA=50，结构参数内环半径r、外环半径R和环柱的高度h为设计变量。根据实际安装的要求，各设计变量的范围分别为：36 mm≤R≤40 mm；30 mm≤h≤40 mm；20 mm≤r≤30 mm。

图2 橡胶悬置软垫的结构简图

根据图2的结构简图，在ABAQUS中进行软垫结构的参数化建模，用Python语言编写批处理子程序。ABAQUS有限元批处理后生成的数据见表1。

用BP神经网络生成神经网络优化函数。构建三层BP神经网络，输入层神经元数目为3，对应橡胶软垫的几何参数R、h和r；中间层神经元数目取为5；输出层神经元数目为2，对应橡胶软垫的刚度Kx和Kz。训练网络参数设定为：允许最大训练步数net.trainParam.epochs =5000，训练目标最小误差net.trainParam.goal=0.01， 学习速率net.trainParam.lr=0.05。网络训练的误差曲线如图3所示。由图3中可知，训练次数越多，网络输出和样本目标越接近一致，较快达到允许误差(10-2)以下。

在用遗传算法优选结构参数时，群体大小取200，交叉率Pc=0.6，变异率Pm=0.09，权重值α1=α2=0.2，α3=0.6，适应度函数取为1/g，适应度在进化过程中的变化曲线如图4所示。最后得到悬置软垫结构参数优化结果为R=35 mm，h=31mm ，r=25mm，对应的ABAQUS有限元计算刚度为Kz= 142.92 N/mm、Kx=Ky=48.95 N/mm，与目标刚度Kmz=150 N/mm、Kmx=Kmy=50 N/mm的误差均小于5%，优化结果符合要求。

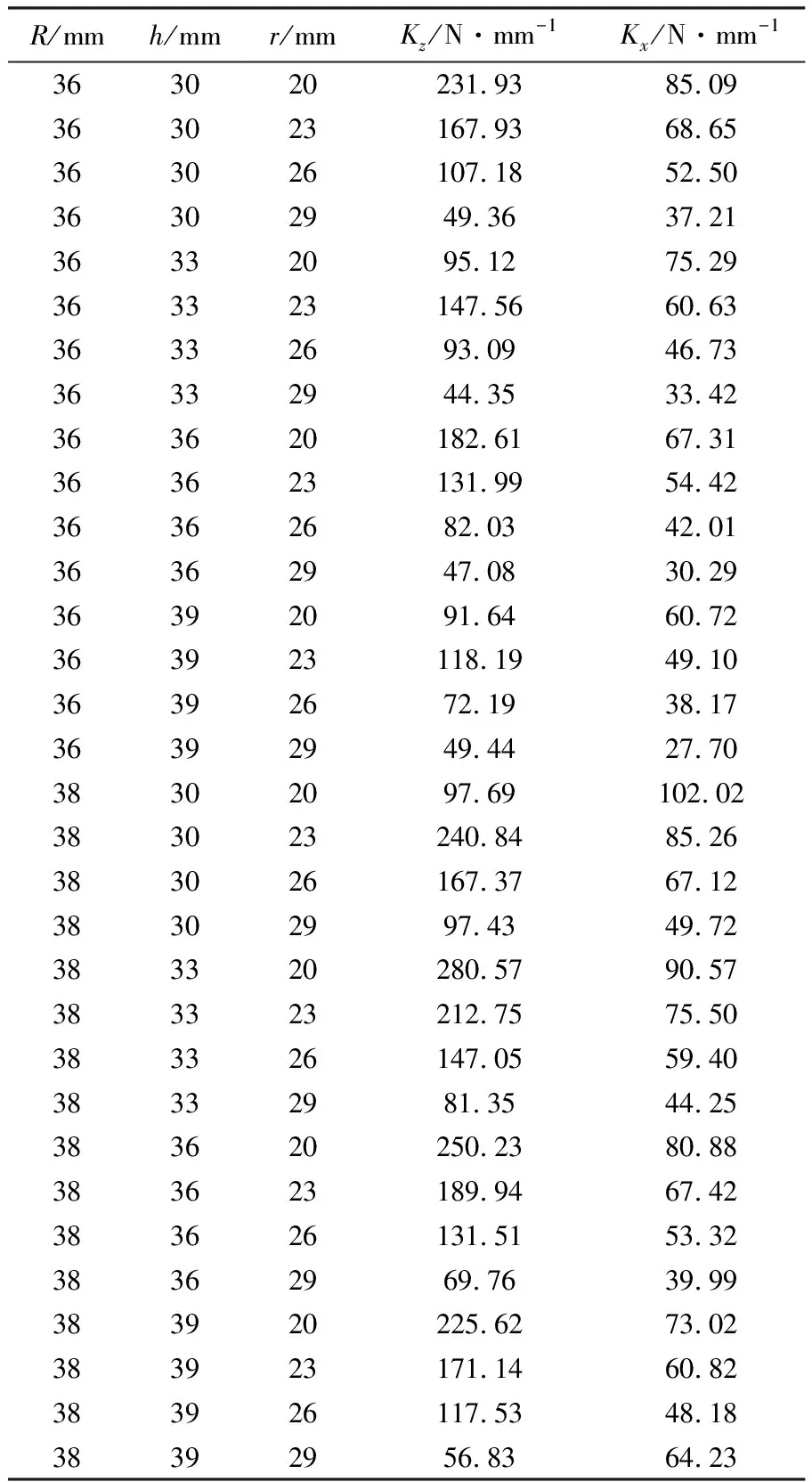
表1 ABAQUS自动生成数据

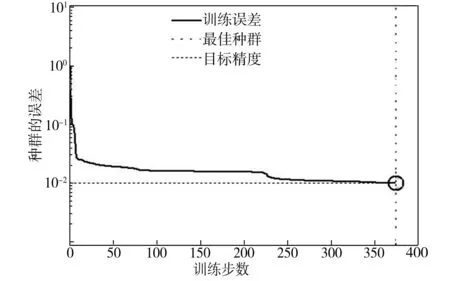
图3 网络误差曲线

图4 适应度曲线

6 结语

本文采用MATLABI平台，以ABAQUS为有限元分析手段，结合BP神经网络和遗传算法，开发了一套悬置软垫结构参数优化系统。通过实例分析，优化结果与实际要求基本一致，表明本悬置软垫结构参数优化系统所采用的原理和方法是可行的。该系统可以根据所提出的三向刚度要求，快速、准确地确定悬置软垫的结构参数，摆脱了繁杂的计算，大大缩短了设计周期，节约了人工和时间成本，能够很好地解决实际中发动机悬置的结构设计问题。

[1] 庞剑，谌刚，何华．汽车噪声与振动——理论与应用[M]．北京：北京理工大学出版社, 2006.

[2] 张健．轻型客车动力总成悬置系统优化设计与研究[D]．武汉：武汉科技大学, 2013．

[3] 陈莲，周海亭．计算橡胶隔振器静态特性的数值分析方法[J]．振动与冲击, 2005, 24(3):120-123．

[4] 赵建才，李堑，姚振强．橡胶悬置元件结构参数优化设计方法[J]．振动与冲击, 2008, 27(1):16-18．

[5] 吴恒亮，代会军．橡胶隔振器设计开发研究[J]．噪声与振动控制, 2009(3):114-116．

[6] 钟同圣，卫丰，王鸷，等．Python语言和ABAQUS前处理二次开发[J]．郑州大学学报：理学版, 2006,38(1):60-64．