密度泛函理论及其在选矿中的应用

何桂春， 蒋巍， 项华妹， 齐美超， 康倩

（江西理工大学资源与环境工程学院，江西 赣州341000）

在选矿领域，多采用通过具体实验辅之以理论分析的方法来分析探究矿物的可选性.比如，人们通过测量矿物吸附浮选药剂的速率、强度、接触角以及浮选溶液中pH值、温度等的变化推断浮选药剂与矿物的作用性质，分析其作用机理.随着科学技术的发展尤其是近代物理技术的发展，各种谱学研究方法如X射线光电子谱（XPS）、紫外光电子谱（UPS）、俄歇电子谱（AES）、二次离子质谱（SIMS）、Rutherford背散射谱（RBS）、红外光谱（IR）、漫反射红外光谱（FDIR）以及溶液溶解作用法、矿物表面酸碱性、电性分析法等为选矿领域的研究带来了极大的方便，解决了一些难题.但是，这些方法仅仅停留在与药剂作用的矿物表面来研究问题，并没有深入的研究矿物的内部结构对浮选产生的影响.近些年来，随着量子化学理论的发展，特别是密度泛函理论的提出和发展成熟以及计算硬件水平的提高，使得通过计算对物质内部结构和微观性质进行探索成为可能[1].

1 量子化学历史回顾

20世纪30年代，德国物理学家海森堡和奥地利物理学家薛定谔各自发表了著名的不确定度关系和薛定谔方程，宣告了量子力学的确立[2-3].1927年，德国物理学家海特勒和伦敦将量子力学的方法处理氢气分子，成功地阐释了两个氢原子之间化学键形成的过程，这标志着量子力学和化学的交叉学科——量子化学的诞生[4-7].之后，化学家们在此基础上，应用量子化学理论，建立了量子化学描述分子结构的三大基础理论：价键理论、分子轨道理论以及配位场理论[8-11]. 1928年，哈特里根据自洽势场的要求提出了Hartree方程；1930年，福克和斯莱特考虑到简单的乘积波函数不满足反对称性的要求，进一步完善了Hartree方程，提出了Hartree-Fock方程；为了求解这一方程，1951年罗特汉进一步发展出了著名的HFR方程[12-14]. HFR方程以及在这个方程基础上发展出的计算方法是现代量子化学处理问题的根本方法.1952年日本化学家福井谦一提出的前线轨道理论和1965年美国化学家伍德瓦尔德和霍夫曼提出的分子轨道对称性守恒理论，使窥探分子轨道波函数等抽象概念得以实现[7，15].

量子力学早在20世纪30年代就已基本建立，虽然可以处理一些电子、原子、分子和固体层次上遇到的一般物理和化学理论问题，但是由于所涉及的多电子体系薛定谔方程求解非常困难，至今仍不能精确求解，即使是近似解，计算量也大得惊人.因此，固体物理的理论计算一直很缓慢，直到20世纪90年代密度泛函理论的成熟和计算硬件的发展，量子理论才为矿物结构及其表面的计算提供了有效的理论工具[16-19].

2 密度泛函理论

在密度泛函理论建立之前，量子理论是基于波函数来展开研究的.波函数是3N个变量的函数（N为体系电子数），人们很难想象出电子波函数的形状.在量子力学建立之前，基于电子密度的理论有效地解释了很多的实验现象和规律，而电子密度仅是3个变量的函数.假如能够用电子密度代替波函数来描述体系的状态和计算体系性质，将给量子力学带来极大的方便.在1927年，Thomas和Fermi提出以动能作为电子密度泛函的表示式的均匀电子气模型，即Thomas-Fermi模型，为密度泛函理论开创了先河，可以看成密度泛函理论的雏形.1951年Slater提出Xα近似，将体系能量表示为电子密度函数的泛函逼近Hartree-Fock方法中离域交换势，可以看作密度泛函理论的前导.但是，现代的密度泛函理论是在1964年Hohenberg和Kohn证明的2个定理的基础上建立的；在1965年Kohn和Sham提出的Kohn-Sham方程为密度泛函理论的应用铺平了道路.

2.1 Thomas-Fermi模型

在1927年，Thomas和Fermi就作了用密度泛函来描述和确定体系的性质而不求助于波函数的尝试，建立了Thomas-Fermi模型[20]，得出电子体系（闭壳层体系）的总能量为：

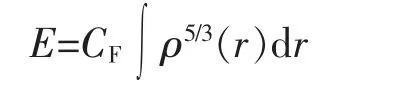
因为上述体系只有动能（V=0），所以体系的总能量即为体系的总动能TTF，即TTF=E.

用于原子体系，得到Thomas-Fermi能量泛函为：

虽然计算出来的ρ（r）与实际ρ（r）接近，但是不能对原子形成分子作出解释.

2.2 Xα近似

1951年Slater出于对减少Hartree-Fock方法计算量的考虑，提出Xα近似方法[21].得到自旋成对的均匀电子气体系的交换势VXα（r）表达式为：

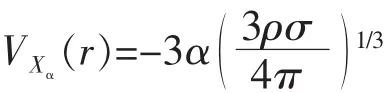
其中σ为电子自旋态；α为可调参数，0.69～0.78；并表明VXα（r）是电子密度分布函数的泛函.

将VXα（r）代替Hartree-Fock总能量表达式中的交换势，即得出总能量的密度泛函表达式.

虽然Xα方法可以看成是一种密度泛函理论，但Slater并没有从证明体系的状态的性质可以用电子密度分布描述的角度出发，而是从减少Hartree-Fock方法的计算量着眼，将Xα看作一种近似计算方法.因此，一般认为密度泛函理论是在Hohenberg和Kohn对2个定理的证明建立起来的.

2.3 Hohenberg-Kohn定理

1964年，Hohenberg和Kohn基于非均匀电子气理论，证明了2个定理[22].

定理1：对于处于外势V（r）中的多电子系统，其基态的电子密度分布与体系所处外势场存在一一对应关系，因此可以确定体系的所有性质.

定理2：对于任意的函数ρ’（r），若满足条件：ρ’（r）≥0，∫ρ’（r）dr=N，则E[ρ’（r）]≥E0，N是体系包含的电子数，E0是体系基态能量.

由定理1可知体系总能量E[ρ]，动能T[ρ]，电子间相互作用能Eee[ρ]都是ρ（r）的泛函，且有：

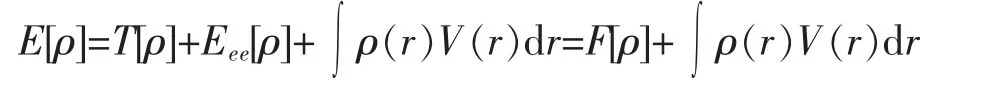
其中F[ρ]＝T[ρ]＋Eee[ρ]

F[ρ]与外势场V（r）无显著关系，为普适性密度泛函.

定理2为计算体系基态能量和电子密度分布提供了一种变分计算方法，按照Lagrange不定乘子变分方法，得Euler-Lagrange方程：

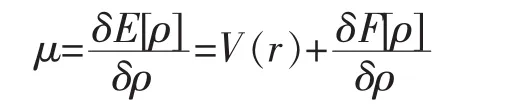
其中F[ρ]与外势V（r）无关，是一个ρ（r）的普适性泛函，如果能够找到它的近似形式，Euler-Lagrange方程就可将用于任何体系，因此，此式是密度泛函理论的基本方程.

然而，Hohenberg-Kohn定理虽然明确了可以通过求解基态电子密度分布函数得到系统的总能量，但并没有说明如何确定电子密度分布函数ρ（r），动能泛函T[ρ]和电子间相互作用泛函Eee[ρ]，直到1965年Kohn-Sham方程的提出，才真正将密度泛函理论引入实际应用.

2.4 kohn-Sham方程

1965年Kohn和Sham提出了Kohn-Sham方程[16]，即：

其中

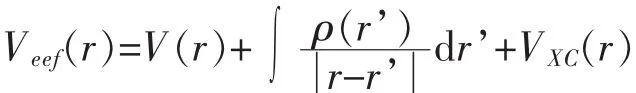
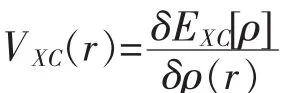
VXC（r）称为交换相关势，知道EXC[ρ]即可求出.求得Kohn-Sham方程即可得基态电子密度ρ（r）和能量E（ρ）.

2.5 交换-相关泛函

由Kohn-Sham方程可知，交换-相关泛函[23]EXC[ρ]在密度泛函理论中非常重要，是求解KS方程的关键.但是到目前为止，EXC[ρ]还没有准确的表达式.找到更精确的交换相关近似一直是密度泛函理论的发展主线.在各种近似方法中用的最广泛的是局域密度近似（LDA）和广义梯度近似（GGA）.

LDA是用通过均匀电子气的密度函数ρ（r）得到系统非均匀电子气交换-相关泛函的具体形式.LDA的提出导致了密度泛函理论的广泛应用.如果在LDA的基础上，进一步考虑不同自旋分量的电子密度，就发展成为自旋极化的局域密度近似LSDA.

GGA用密度的梯度校正了由于电子密度分布不均而导致的误差，使得计算的结果较之于LDA更精确.

3 密度泛函理论在选矿中的应用

在浮选过程中，矿物结构、矿物表面、选矿药剂以及它们之间的相互作用关系是影响浮选技术指标的内在关键因素.随着密度泛函理论的发展成熟和计算机硬件技术的发展，使得通过计算对矿物的结构、表面以及选矿药剂的研究成为可能.通过应用密度泛函理论进行理论计算，对矿物内部结构、表面微观性质、选矿药剂分子进行分析，解释选矿过程中所表现出来的宏观现象，阐述选别的反应机理并对药剂的合成与开发提供指导.

3.1 在矿物表面研究中的应用

运用密度泛函理论计算方法对矿物的表面进行计算，并对计算结果进行分析，可以得到矿物表面微观状态以及解释选矿过程中所表现出的宏观现象.

曾振华等[24]应用密度泛函理论，对O在Au（111）表面上的吸附结构、吸附能、功函数、电子密度和投影态密度进行了研究，给出了O的吸附特性在0.11Ml到1.0Ml覆盖度范围内的变化规律.从计算的结果中可以发现O在Au（111）表面的稳定吸附位是fcc洞位，且在此洞位的吸附能与覆盖度的变化成反比关系.由于Au（111）表面电子的向O的偏移而形成表面偶极子，导致表面功函数的变化率与覆盖度的变化有类似于线性的关系.在O-Au的相互作用下形成成键态与反键态，且2种键态都被金属键占据，造成O-Au键能和吸附能的减弱.

洪汉烈等[25]对吸附在黏土矿物高岭石晶体边缘的含金络合阴离子[Au（Sb2S4）]-与高岭石晶体的成键性质用离散变分Xα方法进行了量子化学计算.根据对络合阴离子[Au（Sb2S4）]-在高岭石晶体基面和侧面不同位置的10个模型的计算，得出络合阴离子[Au（Sb2S4）]-在高岭石侧面的稳定性要好于在基面的稳定性，而且在高岭石晶体侧面时，络合阴离子[Au（Sb2S4）]-与O形成共价键.这就从理论上说明了络合阴离子[Au（Sb2S4）]-在高岭石晶体边缘的吸附是一种化学吸附.

李玉琼等[26]采用基于密度泛函理论的CASTEP软件对理想黄铁矿 （100）表面的结构弛豫、原子Mulliken布局和电子结构进行了计算.计算结果表明黄铁矿（100）面的弛豫主要发生在表面配位不足的铁原子周围，且经历的弛豫较小，没有发生显著的重构现象.硫原子的电荷经历了一个由表面到体相从负到正的过程而铁原子正好相反.黄铁矿（100）面的电子由铁原子转移到了硫原子上，并且在表面的铁-硫原子的相互作用要强于体相中的铁-硫原子的相互作用.由于黄铁矿（100）表面层的能系降低，导致表面具有类似于金属的特征，导电性得到增强，电化学活性也得到提高.

3.2 在矿物结构研究中的应用

利用密度泛函理论，通过计算可以对矿物内部分子结构进行分析，得到矿物内部分子结构对矿物性质表现的影响，对选别过程中的反应机理进行解释.

陈建华等[27]采用密度泛函理论的第一性原理方法，从能带结构及态密度、Mulliken布局和前线轨道3个方面对黄铁矿、白铁矿和磁黄铁矿的电子结构进行了计算分析，并对这3种矿物的电子结构与可浮性之间的关系进行了讨论.能带结果计算表明：黄铁矿和白铁矿属于窄能隙半导体，磁黄铁矿属于金属导体，说明3种矿物在浮选溶液中与药剂的电化学反应具有较大的差异.由态密度分析可知，3种矿物中的铁原子的3 d轨道对费米能级附近的态密度做的贡献大小不同，由大到小依次是黄铁矿、白铁矿和磁黄铁矿，说明在浮选溶液中，3种矿物与氢氧根和氰离子作用的强弱顺序为黄铁矿、白铁矿和磁黄铁矿.从Mulliken布局分析可以得到，黄铁矿与白铁矿晶体内部的Fe与S之间主要是以共价性为主且相近，但是白铁矿中S与S之间的共价性要弱于黄铁矿.磁黄铁矿晶体由于铁原子的作用，呈现较大的离子性.所以在浮选过程中，疏水性强弱的顺序为黄铁矿、白铁矿和磁黄铁矿.前线轨道分析表明3种矿物被氧化的顺序为磁黄铁矿、白铁矿、黄铁矿.因此，3种矿物与黄药作用后表现出的可浮性强弱顺序依次为白铁矿、黄铁矿、磁黄铁矿.

李玉琼等[28]采用密度泛函理论和平面波赝势方法对含天然杂质的黄铁矿的电子结构计算，并讨论了各种天然杂质对黄铁矿催化活性的影响.计算分析结果表明在天然杂质中，过渡金属主要由d轨道产生杂质能级；主族金属及非金属杂质主要由s或p轨道产生.当黄铁矿含有铜、钼、砷、金、银或镍杂质时，将增强黄铁矿对氧的还原电催化能力.钴、镍、金、银等杂质还能增强黄铁矿表面俘获电子的能力.

3.3 在选矿药剂研究中的应用

通过对选矿药剂进行密度泛函理论计算，可以掌握药剂与矿物之间的相互作用，得出同种或不同种类的药剂与矿物的相互作用程度，为选择或者合成选矿药剂提供理论支持.

陈建华等[29]利用密度泛函理论，在 B3LYP/6-31G水平下分别对十二伯胺、十四伯胺、十六伯胺以及十八伯胺的阳离子分子构型进行了优化，得到了4种阳离子的红外光谱频率，静电荷分布状况、偶极矩以及前线轨道能量和组成.分析了伯胺阳离子分子结构与氧化锌浮选性能之间的关系.计算结果分析表明：随着胺阳离子碳链长度的增加，其偶极矩和最高占据轨道能量也随着增大，但是最低占据轨道的能量却基本保持不变.伯胺阳离子碳链长度与氧化锌捕收性能的关系，主要取决于胺的偶极子和矿物之间产生的定向作用力.

刘臻等[30]利用密度泛函理论研究了吸附在云母表面的烷基伯胺对云母表面疏水性的影响.研究结果表明：随着烷基伯胺的碳链的增长，其吸附在云母表面对疏水性能的提高效果越显著.但是，也并不能一味的增长碳链，因为碳链的增长会导致烷基水溶性的下降.所以选择合适的烷基伯胺要综合考虑碳链长度和水溶性的影响.

4 结束语

密度泛函理论已在选矿领域得到广泛的应用，特别是对矿物表面、结构以及选矿药剂的研究，可为选矿工作提供坚实的理论基础，更好地指导选矿工作的展开.

在运用密度泛函理论的KS方程时，选择合适的交换相关泛函是关键.由于密度泛函理论的不完善，在利用密度泛函理论进行研究时，要善于与实际试验相结合，与各种谱学方法相结合.密度泛函理论的计算结果一定要与现实相一致，否则就失去了对选矿工作的理论指导意义.

[1]Foresman J B，Frisch A.Exploring chemistry with electronic structure methods[M].Pittsburgh：Gaussian，Inc.，1996.

[2]陈建华.硫化矿物浮选晶格缺陷理论[M].长沙：中南大学出版社，2012.

[3]赵成大.固体量子化学[M].北京：高等教育出版社，2003.

[4]陈光巨，黄元河.量子化学[M].上海：华东理工大学出版社，2008.

[5]曾谨言.量子化学[M].北京：科学出版社，2000.

[6]陈正隆，孙小强.量子化学[M].南京：南京大学出版社，2007.

[7]Szabo A，Ostlund N S.Modern quantum chemistry[M].New York：Dover Publications，1996.

[8]陈飞武.量子化学中的计算方法[M].北京：科学出版社，2008.

[9]赵成大.量子化学中的场论方法[M].长春：东北师范大学出版社，2007.

[10]林梦海.量子化学计算方法与应用[M].北京：科学出版社，2004.

[11]Kaxiras E，Atomic and electronic structure of solids[M].New York：Cambridge University Press，2003.

[12]徐光宪，黎乐民，王德民.量子化学——基本原理和从头计算法[M].北京：科学出版社，2009.

[13]刘靖疆.基础量子化学与应用[M].北京：高等教育出版社，2004.

[14]林梦海.量子化学简明教程[M].北京：化学工业出版社，2005.

[15]Cramer C J.Essentials of computational chemistry theories and models[M].Chichester：John Wiley&Sons Ltd.，2004.

[16]Kohn W，Sham L J.Self-consistent equations exchange and correlation effects[J].Physical Review，1965，140（11）：1133-1138.

[17]Parr R G，Yang W.Density-functional theory of atoms and molecules[M].London：Oxford University Press，1989.

[18]Perdew J P，Schmidt K.Jacob’s ladder of density functional approximations for the exchange-correlation energy[C]//Doren V V，Alsenoy V C，Geerlings P.Density functional theory and its application to materials：AIP Conference Proceedings.New York：AIP Publishing，2001：1-20.

[19]Perdew J P，Kurth S.Density functionals for non-relativistic coulomb systems in the New Century[J].Lecture Notes in Physics，2003，620：1-51.

[20]Szasz L.Pseudopotential theory of atoms and molecules[M]. New York：John Wiley&Sons Ltd.，1985.

[21]Wood J H，Boring M A.Improved pauli hamiltonian for localpotential problems[J].Physical Review B，1978，18（9）：2701-2711.

[22]Hohenberg P，Kohn W.Inhomogeneous electron gas[J].Physical Review，1964，136（11）：864-871.

[23]Hafner J.Ab-Initio simulations of materials using VASP：Densityfunctional theory and beyond[J].Journal of Computational Chemistry，2008，29（13）：2044-2078.

[24]曾振华，邓辉球，李微雪，等.O在Au（111）表面吸附的密度泛函理论研究[J].物理学报，2006，55（6）：3157-3164.

[25]洪汉烈，闵新民，付正义.含金络合离子[Au（Sb2S4）]-在高岭石表面吸附的量子化学研究[J].矿物学报，2001，21（3）：515-518.

[26]李玉琼，陈建华，陈晔，等.黄铁矿（100）表面性质的密度泛函理论计算及其对浮选的影响[J].中国有色金属学报，2011，21（4）：919-926.

[27]陈建华，钟建莲，李玉琼，等.黄铁矿、白铁矿和磁黄铁矿的电子结构及可浮性[J].中国有色金属学报，2011，21（7）：1719-1727.

[28]李玉琼，陈建华，郭进.天然杂质对黄铁矿的电子结构及催化活性的影响[J].物理学报，2011，60（9）：650-657.

[29]陈建华，陈晔，李玉琼.氧化锌浮选中伯胺阳离子捕收剂的密度泛函理论计算[J].广西大学学报：自然科学版，2009，34（1）：67-71.

[30]刘臻，刘够生，于建国.云母表面吸附烷基伯胺对其疏水性的影响[J].物理化学学报，2012，28（1）：201-207.