鄱阳湖流域年降水量周期、趋势及响应特征分析

谢毅文，张强，李越，罗世豪，陈亚松，陈笠翔

(1.东莞理工学院 化学与环境工程学院，广东 东莞 523808；2.水资源与水电工程科学国家重点实验室，湖北 武汉 430072；3.华南地区水循环与水安全广东省普通高校重点实验室, 广东 广州 510275；4.珠江水利委员会，广东 广州 510611；5.珠江水利委员会 珠江水利科学研究院，广东 广州 510611；6.东莞市海汇环保科技有限公司，广东 东莞,523000)

鄱阳湖流域位于长江中游末段南岸，含赣江、抚河、信江、饶河、修河五河水系和青峰山溪、博阳河、樟田河、潼津河等独流入湖的小河构成独立完整的流域自然地理单元[1]。鄱阳湖流域总面积为16.2×104km2，范围涉及江西、湖南、安徽、福建、浙江、广东六省，其中96.9%的流域面积在江西省内[2]。随着全球气候变暖，水循环加剧，全球范围极端降水事件的发生频率呈增加的趋势[3]，而鄱阳湖流域历年来都受到洪涝、干旱等灾害的困扰，对当地经济社会的可持续发展构成一定障碍[4]。

目前已有多位学者对鄱阳湖流域的降水特征进行了研究。李荣昉等[5]采用小波分析法分析了鄱阳湖流域年降水的周期，发现年降水量周期与厄尔尼诺现象的周期有很好的相关性；霍雨等[6]采用距平分析、Mann-Kendall(M-K)法分析了鄱阳湖流域 1955—2005年的年、季降水特征和变化趋势；郭华[7]采用M-K法分析了1961—2003年间鄱阳湖流域气温、降水量、蒸发量等气候因子的变化趋势。王怀清等[8]采用M-K法分析了鄱阳湖五大流域的年降水量、降雨日数、暴雨日数的变化趋势和突变情况，发现年降水量、暴雨日数呈波动上升趋势。然而从周期、趋势及突变角度综合分析鄱阳湖流域年降水量与年径流量之间的响应关系的研究比较少。

本文综合Morlet小波分析法、M-K法、累积距平法分析鄱阳湖流域年降水量的周期变化和趋势突变特征，进一步探讨年降水量与年径流量在周期、趋势及突变上的响应关系，以期为鄱阳湖流域防洪抗旱及水资源可持续开发利用提供一些科学参考依据。

1 数据来源及研究方法

1.1 数据来源

本文数据主要为鄱阳湖流域内16个气象站的逐日监测降水数据，数据主要年份为1953—2010年；由于部分站点缺失少数年份的数据，这些站点则通过临近站点插补延长获得等时间长度的数据，气象站点名称和地理位置见图1。

1.2 Morlet小波分析法

Morlet小波变换在气象数据多周期分析中已经有了广泛的应用，本研究采用Morlet 小波分析时间序列的时频特征[9-12]。小波分析法不仅可以识别气候资料序列的多时间尺度演变特性，还能检测出气候变化不同层次的突变点位置，以及分析气候变化不同层次的冷暖、干湿结构[13-14]。

为了减小小波分析的边界效应，将资料向前和向后各延拓一个样本长度，变换后再舍弃延拓部分，具体处理方法[15]如下。

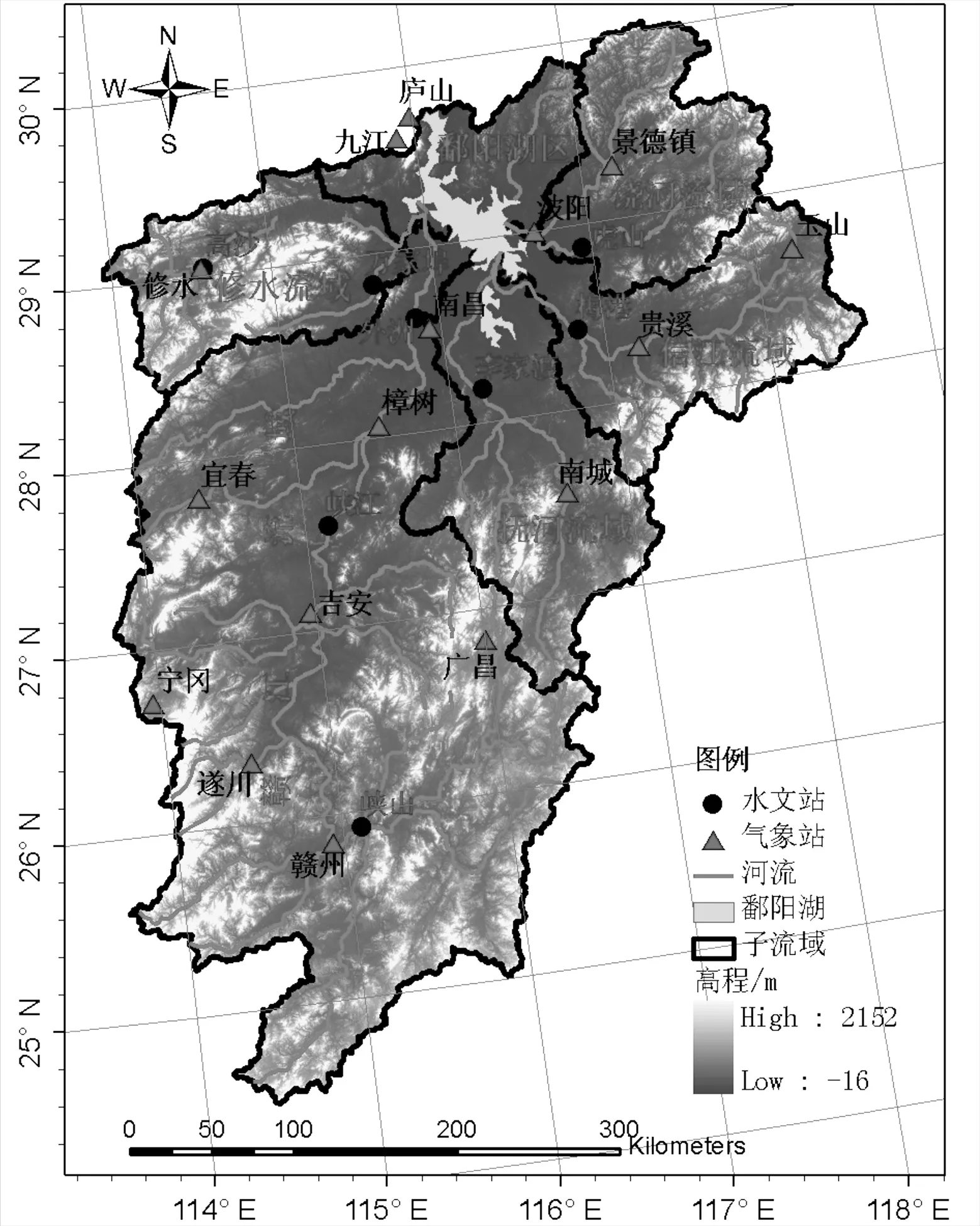
图1 鄱阳湖流域气象站地理位置图

设资料序列为：

X(t)={X(1),X(2),…,X(N)}

(1)

式中，N为样本长度，X(N)为第N个资料。

向前延伸N个资料：

X(-t)=X(t+1)t=1,2,…,N-1

(2)

向后延伸N个资料：

X(t+N)=X(N+1-t)t=1,2,…,N

(3)

通过小波方差检验各序列的主要周期(对序列变化起主要作用的周期)，小波方差计算公式为：

(4)

式中，a为频率参数，b为时间参数，Wp(a)为小波方差，Wf(a,b)为小波系数。

1.3 Mann-Kendall法

Mann-Kendall法是一种能够检测序列的趋势变化是否发生突变，并指出突变开始时间及突变区域的非参数统计检验方法，具有不需要样本遵从一定的分布和不受少数异常值干扰的优点[16]。

2.1.1 诊断食管狭窄时超细鼻胃镜的通过率 在单纯诊断性检查食管狭窄性病变中，超细鼻胃镜的通过率在食管癌引起的狭窄中为81.58%，在食管术后吻合口良性狭窄和复发中的通过率分别为77.78%和100.00%，食管外压性狭窄中的通过率为75.00%，不明原因性狭窄40.00%，总通过率为76.92%(表2)。

在趋势分析上，统计参数M值反映趋势变化的方向和显著程度。若M值为正值，表示序列呈增长趋势，M为负值则表明呈下降趋势；且M值的绝对值越大，趋势越显著，置信度越高。设气候序列为:

xi=(x1,x2, … ,xn)

式中n为样本长度。

定义M值如下：

M=

(5)

其中RANK(xi,xi:xn, 0)为EXCEL软件中的排序函数。

在突变分析上，设x为具有n个样本量的时间序列，构造秩序列Sk：

(6)

(7)

秩序列Sk是第i时刻数值大于第j时刻数值个数的累计数。

假定时间序列为随机独立的，定义统计量UFk：

(8)

其中，E(Sk)、var(Sk)分别是累计数Sk的均值和方差；UFk是按时间序列x顺序x1，x2，…，xn计算出的统计量序列，为标准正态分布。

在给定显著性水平a的条件下，查正态分布表，若│UFk│>Ua，则表明序列的趋势变化明显。UBk是按时间序列x逆序xn，xn-1，…，x1计算出的统计量序列，且UBk=-UFk(k=n，n-1，…，1)，UB1=0。本文在给定显著性水平a=0.05(临界值u0.05=±1.96)的情况下，绘制Mann-Kendall统计量曲线。UFk或UBk值小于0表明序列呈下降趋势，大于0则表明呈上升趋势。当UFk或UBk值超过临界值时，表明下降或上升趋势显著。若UFk和UBk两条曲线在临界线之间出现交点，则交点对应的时刻为突变开始的时间[13]。同时采用u检验法检验突变的显著性，并以累积距平法验证突变点的有效性。

2 周期分析

2.1 小波变换系数模平方时频特征分析

对鄱阳湖流域年降水量进行距平(中心化)标准化处理，再作Morlet小波变换。Morlet小波系数模的大小反映特征时间尺度信号的强弱，模平方越大表明对应尺度和时段的周期性越显著。图2为鄱阳湖流域年降水量距平序列的Morlet小波变换系数的模平方时频分布图。分析不同时段各时间尺度的强弱分布，得出20～25 a时间尺度信号能量变化最强，具有全域性，振荡中心在1976年；6～8 a时间尺度信号能量变化较强，主要发生在1953—1989年，振荡中心在1974年左右；其次3～5 a时间尺度信号则在1953—1974年及1996—2010年期间表现明显；12～15 a时间尺度信号在1980—2010年表现明显，其余时间尺度信号能量变化较弱。可见，大时间尺度(10～25 a)年代际周期振荡在整个时间域中明显偏后，而相对的小时间尺度(3～8 a)在整个时间域中偏前。由此可知，在1953—2010年期间，鄱阳湖流域的降水量周期变化表现为大周期特征比小周期特征显著，且存在大周期特征加强的趋势。

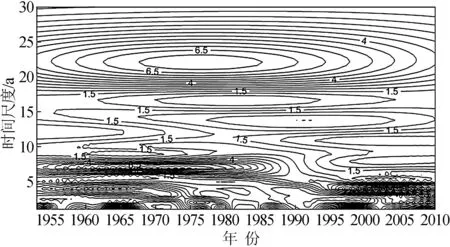
图2 Morlet小波变换系数模平方时频分布

2.2 小波变换系数实部时频特征分析

不同时间尺度下的小波变换系数可以反映系统在该时间尺度下变化特征：正的小波系数对应于偏多期，负的小波系数对应于偏少期；小波系数绝对值越大，反映对应时间尺度变化越显著。图3为鄱阳湖流域年降水量距平序列Morlet小波变换系数的实部时频分布图，图中清晰地显示了年降水量时间尺度变化及其位相结构。

图3 Morlet小波变换系数实部时频分布

图3中，20～25 a周期震荡非常显著，其中心时间尺度为22 a，鄱阳湖流域年降水经历了约3个由多到少的循环交替。12～15 a周期震荡也比较显著，在1961—2009年经历了3.5个由少到多的循环交替；6～8 a周期震荡在整个时间域表现为逐渐减弱；3～5 a则在1974年之前和在1994年之后表现较强，在1974—1994年期间则明显削弱。从大尺度来看，鄱阳湖流域年降水量在1953—1959年、1971—1981年及1992—2001年间偏多；在1960—1970年、1982—1991年及2002—2010年间偏少。从8 a以下的小尺度来看，则有更多的降水偏多期和偏少期的循环交替。

2.3 年降水量序列主要周期分析

小波方差反映了波动的能量随时间尺度的分布情况。绘制年降水量时间序列的小波方差图(见图4)，可判断一个降水时间序列中存在的主要时间尺度(主周期)。图4表明鄱阳湖流域年降水量序列存在4个明显峰值，其中最大峰值对应的时间尺度为22 a，表示22 a为鄱阳湖流域年降水变化的第一主周期；同理，第二峰值对应的时间尺度为7 a，7a为第二主周期；第三峰值对应的时间尺度为4 a，4 a为第三主周期；14 a时间尺度对应第四峰值，14 a为第四主周期，由于第四峰值很弱，可视为小波方差值的小波动，予以忽略。由此得出，第一、第二、第三主周期的波动控制着年降水量在整个时间域内的变化特征。

图4 鄱阳湖流域年降水量小波变换方差

图5为以第一、第二、第三主周期绘制出控制鄱阳湖流域年降水量演变的小波系数图。

图5 鄱阳湖流域年降水量主周期

小波系数为正的年份为多雨期，为负的年份为少雨期。从第一主周期(22 a)曲线看，鄱阳湖流域年降水量在1953—2010年经历了2个半的多～少交替变化；从第二主周期(7 a)曲线看，则经历了7个的多～少变化；从第三主周期(4 a)曲线看，则经历了13个多～少变化。

3 趋势突变分析

3.1 趋势分析

计算得出，鄱阳湖流域整体M值为1.214，小于置信度90%检验值1.64，显示鄱阳湖流域年降水量呈不显著的增长趋势。图6为鄱阳湖流域年降水量和年径流量M值空间分布图。由图6可见，流域内16个站点的M值均为正值，其高值中心出现在樟树气象站，并向四周扩散递减。樟树气象站的M值达到2.817，大于置信度99.9%检验值2.807。

图6 鄱阳湖流域年降水量和年径流量M值空间分布图

3.2 突变分析

分析鄱阳湖流域58 a长序列年降水量M-K统计量曲线(图7)可知，UFk曲线在1958—1961年和1964—1968年间都超出显著性水平检验线，而且与UBk曲线在1992年相交于两检验曲线之间，说明在1992年年降水量发生了显著性突变，置信度为95%。对鄱阳湖流域58 a长序列年降水量进行累积距平分析，绘制鄱阳湖流域年降水量累积距平曲线见图8。由图8得出，累积距平曲线在1992年前后由负距平明显转变为正距平，其转折点与M-K法得出的突变点位置基本一致，验证了M-K法检验突变的结果。

图7 鄱阳湖流域年降水量M-K统计量曲线

图8 鄱阳湖流域年降水量累积距平曲线

3.3 年降水量与年径流量响应关系分析

根据叶许春等研究[4]显示(见表1)，鄱阳湖流域五河水系年径流量整体呈增长趋势，其中90年代增长幅度最为显著，突变点发生在1992年[4]。该研究结果与本研究得出的鄱阳湖流域年降水量呈不显著的增长趋势并在1992年发生显著性突变是基本对应的。分析图6可得，鄱阳湖流域内各水文站点的年径流量M值与降水量M值在空间分布上比较一致，基本呈年降水量M值越大的区域，其年径流量M值越大，反之亦然。显示鄱阳湖流域年径流量趋势变化与年降水量存在显著的响应关系。

同时，根据刘健等[17]等采用小波分析法研究鄱阳湖流域主要水系近50 a径流变化得出第一主周期25～26 a、第二主周期8 a、第三主周期3～4 a，与本研究得出鄱阳湖流域年降水量序列主周期(第一主周期22 a、第二主周期7 a、第三主周期4 a)是基本对应的。由于鄱阳湖流域年降水量与年径流量在趋势突变以及周期变化在尺度范围、时间点位以及显著程度均比较一致，可见鄱阳湖流域年径流量与年降水量之间存在显著的响应关系。

表1 鄱阳湖流域代表站点年径流量的变化趋势检验[4]

4 结 论

1) 基于小波变换分析得出，鄱阳湖流域年降水量序列存在3个主周期，分别为第一主周期22 a，第二主周期7 a，第三主周期4 a，三者的波动控制着年降水量在1953—2010年的变化特征。

2) 采用M-K法进行趋势突变分析得出，鄱阳湖流域16个站点的年降水量序列M值均为正值，其高值中心出现在樟树气象站，流域年降水量整体呈不显著的增长趋势。分析M-K统计量曲线得出，鄱阳湖流域年降水量在1992年发生显著性突变，置信度为95%。采用累积距平曲线进行验证分析得出，累积距平曲线转折点与M-K法得出的突变点均发生在1992年。

3) 对比鄱阳湖流域年降水量与年径流量的时空特征得出，鄱阳湖流域年降水量与年径流量的周期变化和趋势突变在尺度范围、时间点位、空间分布及显著程度均比较一致，显示鄱阳湖流域年降水量与年径流量之间在周期、趋势和突变方面存在显著的响应关系。

参考文献：

[1] 王晓鸿,鄢帮有,吴国琛.山江湖工程[M]. 北京:科学出版社,2006.

[2] 金斌松,聂明,李琴,等.鄱阳湖流域基本特征面临挑战和关键科学问题[J]. 长江流域资源与环境,2012, 21(3):268-275.

Jin binsong, Nie Ming, Li Qin, et al. Basic characteristics, challenges and key scientific questions of the Poyang Lake Basin[J]. Resources and Environment in the Yangtze Basin, 2012, 21(3):268-275.

[3] 陈秀万.中国洪水灾害分析[J]. 海洋地质与第四纪地质,1995, 15(3):161-168.

Chen Xiuwan. Analysis on flood disasters in China[J]. Marine Geology & Quaternary Geology, 1995, 15(3):161-168.

[4] 叶许春,张奇,刘健,等.鄱阳湖流域天然径流变化特征与水旱灾害[J]. 自然灾害学报,2012, 21(1):141-147.

Ye Xuchun, Zhang Qi, Liu Jiang, et al. Natural runoff change characteristics and flood /drought disasters in Poyang Lake catchment basin[J]. Journal of Natural Disasters, 2012, 21(1):141-147.

[5] 李荣昉,王鹏,吴敦银.鄱阳湖流域年降水量时间序列的小波分析[J]. 水文,2012, 32(1):29-31.

Li Rongfang, Wangpeng, Wu Dunyin. Wavelet analysis of annual precipitation series in Poyang Lake basin[J]. Journal of China Hydrology, 2012, 32(1):29-31.

[6] 霍雨,王腊春,陈晓玲,等.1950s以来鄱阳湖流域降水变化趋势及其持续性特征[J]. 湖泊科学,2011, 23(3):454-462.

Huo Yu, Wang Lachun, Chen Xiaoling, et al. Long-term trend and persistence of precipitation over Lake Poyang basin since 1950s[J]. Journal of Lake Sciences, 2011, 23 (3):454-462.

[7] 郭华,姜彤,王国杰,等.1961—2003年间鄱阳湖流域气候变化趋势及突变分析[J]. 湖泊科学,2006, 18(5):443-451.

Guo Hua, Jiang Tong, Wang Guojie, et al. Observed trends and jumps of climate change over Lake Poyang basin, China: 1961—2003[J]. Journal of Lake Sciences, 2006, 18 (5):443-451.

[8] 王怀清,赵冠男,彭静,等.近50年鄱阳湖五大流域降水变化特征研究[J]. 长江流域资源与环境,2009, 18(7):615-619.

Wang Huaiqing, Zhao Guannan, Peng Jing, et al. Percipitions characteristics over five major river systems of Poyang Drainage Areas in recent 50 years[J]. Resources and Environment in the Yangtze Basin, 2009, 18 (7):615-619.

[9] Christopher T, Gilbert P C. A practical guide to wavelet analysis[J]. Bulletin of the American Meteorological Society, 1998,79(1):61-78.

[10] Jevrejeva S, Moore J C, Grinsted A. Influence of the Arctic oscillation and El Nino-Southern Oscillation(ENSO) on ice conditions in the Baltic Sea: the wavelet approach[J]. Journal of Geophysical Research, 2003, 108 (D21):4677.

[11] Hua Yi, Hong Shu. Theimprovement of the Morlet wavelet for multi-period analysis of climate data[J]. Journal of Comptes Rendus Geoscience, 2012, 344(1):483-497.

[12] 李艳玲,畅建霞.基于Morlet小波的径流突变检测[J]. 西安理工大学学报,2012, 28(3):322-325.

Li Yanling, Chang Jianxia. Detection of the abrupt changes in runoff based on the Morlet wavelet[J]. Journal of Xi’an University of Technology, 2012, 28(3):322-325.

[13] 魏凤英.现代气候统计诊断预测技术[M]. 北京:气象出版社,1999.

[14] 王红瑞,叶乐天,刘昌明.水文序列小波周期分析中存在的问题及改进方式[J]. 自然科学进展,2006, 16(8):1002-1008.

Wang hongrui, Ye letian, Liu changing. The problems and improved methods of the period analysis of hydrological time series based on the wavelet[J]. Progress in Natural Science, 2006, 16(8):1002-1008.

[15] 王兆礼,陈晓宏,黄国如,等.东江流域汛期降雨序列的小波分析[J]. 人民长江,2010, 41(2):52-55.

Wang Zhaoli, Chen Xiaohong, Huang Guoru, et al. Wavelet analysis of rainfall series during flood season in Dongjiang River Basin[J]. Yangae River, 2010, 41(2):52-55.

[16] 肖莞生,陈子燊.广东沿海降水长期变化特征与极值分析-以汕尾、广州、阳江3市为例[J]. 热带地理,2010, 30(2):135-140.

Xiao Guansheng, Chen Zishen. Analysis of the characteristics and extreme value of rainfall in three coastal cities of Guangdong Province[J]. Tropical Geography, 2010, 30(2):135-140.

[17] 刘健,张奇,许崇育,等.近50年鄱阳湖流域径流变化特征研究[J].热带地理, 2009, 29(3):213-218.

Liu Jian, Zhang Qi, Xu Chongyu, et al. Characteristics of runoff variation of Poyang Lake watershed in the past 50 years[J]. Tropical Geography, 2009, 29(3):213-218.