和田玉超声波深孔珩磨运动特性分析

罗树丽 刘新英 胡 灿 廖结安*

(1 塔里木大学机械电气化工程学院， 新疆 阿拉尔 843300)(2 新疆维吾尔自治区普通高等学校现代农业工程重点实验室， 新疆 阿拉尔 843300)

1 研究背景

和田玉由透闪石Ca2(Mg,Fe2+)5[Si8O22](OH)2微粒矿物集合体组成[1-2],主要为致密块状构造,质地细腻；结构形状主要为毛毡状变晶结构,其次为放射状变晶结构和纤维状柱状变晶结构。和田玉的摩氏硬度为6. 5～6. 9，和田玉韧度极大(韧度也称为研磨硬度)，和田玉的研磨硬度可以达到摩氏硬度为9。中国有一句俗话“玉不琢，不成器”，说明玉石只有经过巧妙构思和精雕细刻，才能最大限度体现其昂贵的艺术价值和商业价值。玉石雕刻工艺中钻孔是极为重要一环，目前常用的钻孔方式有机械式钻孔和超声波振动钻孔，加工质量和精度有待提高，需要进一步抛光；超声波振动深孔珩磨技术能够有效对高硬度、高韧性材料深孔抛光加工[2-8]；因此展开针对和田玉超声波振动深孔珩磨加工系统的设计具有重要社会和经济意义。本文基于和提高田玉深孔加工表面质量要求，对超声波振动深孔珩磨加工运动特性进行建模与计算分析，有利于探索超声振动优化工艺规律，为今后对具体研磨过程提供参考。

2 和田玉超声波振动深孔珩磨系统简介

1—深孔珩磨机床, 2—工件, 3—中心架, 4—超声振动深孔珩磨振动装置, 5—尾座, 6—超声波发生器

超声振动深孔珩磨系统总体结构如图1所示。系统由深孔珩磨机床、工件、中心架、超声波振动深孔珩磨振动装置、尾座和超声波发生器组成，采用卧式内圆磨加工方式。工作时，工件2与主轴一起进行圆周旋转运动，超声振动深孔珩磨振动装置4末端油石在进行相对旋转运动的同时，作轴向的振动，振动的幅值大小与振动频率由超声波发生器6给定可调。

3 超声波振动深孔珩磨加工的运动特性

3.1 和田玉超声波振动内圆珩磨特性

在进行和田玉超声波振动珩磨时，按照超声波的振动方向可分为轴向振动、径向振动和扭转振动。由于超声波轴向振动更利于普通加工机床的改造，本文主要研究轴向振动超声振动深孔珩磨。利用超声波振动装置在珩磨头上施加可控的轴向振动，使其形成与普通深孔珩磨不同的珩磨机理，产生一些独特的珩磨性能。在磨削过程中，当工件以转速n转动时，油石相对于机床以转速n进行相对旋转运动，因此，可以将工件圆周运动与油石的超声波振动进给进行合成，油石进行相对旋转运动。计算时可将工件的旋转运动与油石进给进行迭加，视为油石在作相对旋转运动的同时，进行超声波轴向振动进给。图2所示为轴向超声波深孔珩磨的基本模型。

根据图2所示的轴向超声波振动深孔珩磨运动模型，在磨削过程中，工件以转速n转动时，油石在超声波设定频率f作用下以振幅a作轴向磨削振动，油石的往复速度为油石磨削时的进给量Vf。根据深孔振动钻削的机理，可知油石轴向振动的位移方程为：

Zp=Asin(2π×f×t)

(1)

图2 轴向超声波振动深孔珩磨运动示意图

则可计算钻头随时间变化的运动方程，代入油石圆周位移转角与时间的关系式β=2πnt/60则可知m个曲面的油石的运动轨迹的关系表达式：

k=(1,2,…,m)

(2)

公式(2)中，a——轴向振动钻削振幅，mm；

f——振动频率，HZ；

θ——油石圆周位移转角，rad；

Vf——油石磨削每转进给量，mm/rev；

n——工件转速，rev/min。

由式(2)，可得出超深波振动珩磨内磨圆加工方式时m个曲面油石的运动轨迹如图3所示。

图3 超深波振动珩磨m个曲面油石的运动轨迹图

由图3可看出，在超深波振动珩磨运动时，油石两条相邻的磨削轨迹从开始的平行到磨削接触工件时发生周期性的变化。这表明油石的磨削轨迹能够实现分离型磨削，即磨削时油石与工件的接触并不总是连续的，而是一种振动幅值可调的动态的分离过程。与普通的连续性磨削过程相比较，分离型磨削可以通过调整超深波振动的幅值、振动频率、油石往复速度、主轴的转速来控制磨削的整体性能，达到最佳的理论珩磨工艺要求。

3.2 轴向超声波振动深孔珩磨变速特性

图4 轴向速度dz与切削速度合成简图

根据公式(1)、(2)可知油石的轴向速度dz与圆周方向的磨削速度Vt关系简图如图4所示，其中Va为合成速度，βa为油石与工件间的工作角度。

则轴向超声波振动深孔珩磨的合运动为：

(3)

式中 va——合成切削速度，m/s；

y′——油石振动速度，y′=2πaf，m/s；

vt——深孔珩磨圆周速度，vt=πDn，m/s；

D——工件内径，mm；

3.2.1 频转比参数ω对磨削速度的影响

为了能更清楚地表达超声波振动频率f与工件转速n对磨削速度了影响，定义一个频率与转速比参数ω=60f/n，同时引入油石圆周位移转角与时间的关系式，代入式(3)中可得

(4)

图5 频转比ω参数对磨削速度变化的影响

在分析频转比参数ω对磨削速度的影响时，对公式(4)其余参数进行赋值(a=0. 06 mm，ω=3. 33,D=30 mm,Vf=0. 02 mm),通过数值计算与分析，可得出如图5所示的一个3 600周期内ω参数对磨削速度变化的影响。图5中，实线表示ω=3. 5时的磨削速度曲线，虚线表示ω=3. 11～4. 0时的磨削速度曲线。从图中可以明显看出，参数ω的取值对磨削速度有明显的变化，当ω的取值增大时磨削速度的上限值明显增大，速度变化的频率也有所增加，在一定的合理取值范围内，其余参数不变的情况下，磨削速度的变化与ω的取值呈线性增加的变化关系。

加工时，磨削速度大小和方向均是周期性不断来回变化的，说明在超声波振动磨削时，轴向的超声波振动对磨削速度产生了变化影响，通过速度的不同变化，能对玉石等材料加工时磨削力的影响变化，从而实现以柔克刚的精细珩磨效果。

图6 超声波振幅a参数对磨削速度的变化影响

3.2.2振幅参数a对磨削速度的影响

同样，根据公式(4)，对其余参数进行赋值(ω=3. 33,D=30 mm,Vf=0. 02 mm)控制振幅a的合理变化，可得到如图6所示的超声波振幅参数a对磨削速度的变化影响曲线。图中，a的变化值从a=0. 05～0. 088之间变化，实线代表a=0. 065时的磨削速度变化曲线，虚线代表不同a的取值对磨削速度的影响变化。图6中可看出，振幅参数a对磨削速度的变化影响主要体现在速度大小的变化，在a=0. 05～0. 088时，a与磨削速度呈线性关系。

3.3 轴向超声波振动深孔珩磨变角度特性

普通磨削加工时，油石上各点受力情况和磨削频次存在很大差异，磨削加工时极易形成凹陷，影响磨削加工性能，磨削时油石与工件之间的工作角度的合理控制能有效控制油石凹陷。但在普通磨削加工时，油石与工件之间的磨削是连续的非分离形磨削，工作角度基本上是不发生变化的，这不利于磨削加工性能的整体提高。在超声波振动磨削加工时，油石与工件之间的工作角度是不断发生变化的。在一个油石的旋转周期内，油石的工作角度依次从不变——变大——不变——变小——不变的动态变化过程。同时变化的大小与超声波的振幅参数a、频转比参数ω的大小变化紧密相关。

根据公式(1)、(2)以及图4磨削的轴向速度dz与油石圆周方向的切削速度Vt关系简图可计算磨削时的动态工作角度βa。

(5)

公式(5)中，αh为油石凹陷时的修正角度，取80～100，代入参数(D=30 mm,Vf=0. 02 mm)，可得到频转比ω、振幅a参数对磨削工作角度的影响规律，如图6所示。从图6中可看出，随着振幅的减小与增大，磨削工作角度也随之逐渐减小与增大；同时，从图7中也可看出，ω参数的增加，能使磨削角度的最小值与最大值均增大。这样，调整合适参数，能改变磨削时油石与工件切入时的工作角度，达到珩磨变角度性能，从而提高整体的磨削工艺，有效控制因油石凹陷所带来的磨削工艺误差。

4 结论

通过对超声波振动深孔加工的力学建模与运动轨迹的计算与分析，并对超声波振动深孔磨削时的变速度特性与变角度特性进行了深入的计算与数值分析后，得出了磨削参数对珩磨加工运动的影响规律：

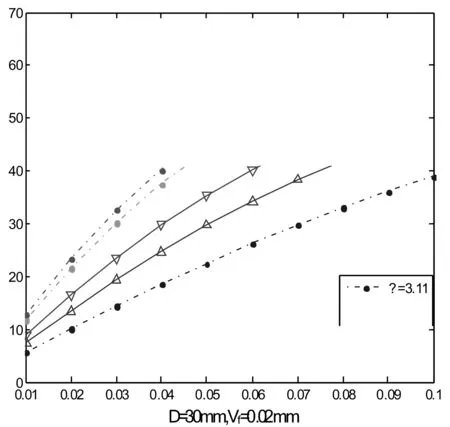
图7 频转比ω、振幅a参数对磨削工作角度的影响

4.1 频转比参数ω的取值对磨削速度有明显的变化，当ω的取值增大时磨削速度的上限值明显增大，速度变化的频率也有所增加，在一定的合理取值范围内，其余参数不变的情况下，磨削速度的变化与ω的取值呈线性增加的变化关系。

4.2 振幅参数a对磨削速度的变化影响主要体现在速度大小的变化，在a=0. 05～0. 088时，a与磨削速度呈线性关系。

4.3 超声波振动磨削时，调整合适参数，能改变磨削时油石与工件切入时的工作角度，这样能有效控制油石的凹陷，增加油石的耐用度，有利于探索超声振动优化工艺规律，为今后对具体研磨过程提供参考。

[1] 吴瑞华，李雯雯，白峰．新疆和田玉岩石学特征及其扫描电镜研究[J]．岩石学报，1999，15(4)：638-644．

[2] 秦娜．旋转超声波磨削制孔的切削力建模与实验研究[D]．大连：大连理工大学，2011．

[3] Qin na, Per Z J, Fisher G R.Simultaneous double-side grinding of silicon wafers:are view and analysis of experimental investigation[J].Machining Science and Technology，2009，13(3):285-316.

[4] 郑书友，冯平友，徐西鹏．旋转超声加工技术研究进展[J]．清华大学学报，2009，19(11)：1799-1803．

[5] Li Hua, Zhang Zhiwei, Zhen Yin. Research and development of ultrasonic vibration internal grinding technology[J].Key Engineering Materials, 2011, 23(4):455-625.

[6] Nomura M, Wu Y.Investigation of internal ultrasonically assisted grinding of small holes:effect of ultrasonic vibration in truing and dressing of small CBN grinding wheel[J]. J.Mech.Sci. Tech,2007, 21(10):1605-1611.

[7] 郑新建．陶瓷型面的数控展成蠕动进给超声波磨削技术的基础研究[D]．南京：南京航空航天大学，2007．

[8] Zhao W S, Wang Z L,Di S C,et al. Ultrasonic and electric discharge machining to deep and small hole on titanium alloy[J]. Journal of Materials Processing Technology, 2002,120(2):101-106.