裂隙密度对快、慢横波速度影响的物理模型实验研究
魏建新,狄帮让,王玲玲,丁拼搏
(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京102249;2.中国石油大学(北京)CNPC物探重点实验室,北京102249)
在裂隙性油气储层的地震勘探和开发中,裂隙参数如密度、方向和充填物等是主要研究对象。在长波长假设条件下,定向排列的裂隙介质具有较强的速度各向异性,其中横波的各向异性对裂隙密度有较强的敏感性。Crampin等[1-2]最早发现岩石各向异性与横波分裂间的关系,Li[3]利用转换波勘探等方法预测实际地层的裂隙密度,使人们认识到建立裂隙密度与横波速度关系的重要性。
已有许多理论和实验研究了裂隙参数(密度、方向、裂隙纵横比)对速度的影响。Hudson[4-5]给出了一个裂隙理论模型,在一定的假设条件下,把裂隙的一些基本参数如裂隙密度、裂隙纵横比等与裂隙介质的弹性参数和速度联系起来。此理论假设裂隙间彼此是隔离的,流体不能流动,裂隙内的压力是未平衡和绝热的。理论模型的估算结果与高频波(超声)条件下的岩样测试结果较符合。Ass’ad等[6-8]用嵌入软物质圆薄片构建的裂隙模型进行了裂隙密度和纵横比对裂隙介质纵、横波速度影响的系列实验研究,实验结果的分析认为裂缝密度小于7%时得到的测试值与理论值基本符合,大于7%时有较大差异,甚至出现横波各向异性随裂隙密度下降的现象。然而,魏建新[9-10]用裂隙密度大于7%的裂隙模型测试表明,横波各向异性与理论值的变化趋势一致,但偏差较大;在用相同裂隙密度不同裂隙尺度模型的实验中发现,横波速度各向异性随裂隙尺度增大而减小。两次实验结果均表明在对裂隙模型的测试中裂隙尺度参数对速度和介质各向异性的影响明显。Rathore等[11]用人工裂隙砂岩实验表明,干燥状态时P波和S波速度(100kHz)与方位角的定性关系与Hudson模型和Thomsen模型一致,饱和水后的实验结果与Thomsen模型相符。
由以上研究结果可以看出,有关Hudson理论的一些实验结果与理论还存在一定的差异,甚至相同的实验方法所得结果也有不同,表明相应的实验研究中还存在某些不足。分析上述文献中的实验方法和结果发现,已有的实验没有较充分地考虑模型和裂隙尺度与波长(或测试频率)的关系,可能是引起实验测试值与理论计算值偏差的一个因素。
我们通过使用较小尺度裂隙充填物制作不同裂隙密度的一组物理模型,同时用3种横波频率(0.50,0.25,0.10MHz)改变波长的方式,观测裂隙密度模型平行和垂直裂隙方向上传播的快、慢横波速度,并与Hudson理论估算值进行对比,分析实验测试值与理论计算值差异的原因,以及波长与裂隙尺度比对快、慢横波速度的影响。
1 实验方法
1.1 裂隙密度模型构建
按Hudson理论中的假设条件采用嵌入法构建裂隙密度模型[12],模型基质用密度为1.182×103kg/m3环氧树脂材料分层制作。每层嵌入低速薄币型裂隙圆片充填物,改变每层嵌入的裂隙片数得到9个不同的裂隙密度模型(图1)。表1给出了9个裂隙密度模型的基本参数,模型的裂隙密度是由裂隙模型外形体积(V),裂隙片半径(r)和总个数(N),通过公式ε=Nr3/V计算得出。表1中M9模型裂隙密度最大,为12%;M1模型裂隙密度最小,为0(表示模型中无裂隙),此模型代表了裂隙模型的基质特性。裂隙模型外表尺寸基本一致,体密度随裂隙密度增大略有下降。

图1 裂隙密度模型及其中裂隙分布示意(a)和模型实物外观照片(b)
低速薄币型裂隙圆片由块状的环氧树脂/硅橡胶混合材料加工而成,密度为1.088×103kg/m3。裂隙圆片直径3mm,是依据模型的大小、裂隙的分布和间距、裂隙密度和测试频率等因素而确定的。图2给出了裂隙薄圆片形状及其厚度分布,圆片厚度在0.07~0.17mm间呈高斯分布,平均值为0.12mm,纵横比为0.040。裂隙圆片随机均匀分布在模型的X-Y平面内(图1a),形成定向稀疏分布的裂隙层,在Z方向共嵌入34层裂隙片(平均层厚约1.714mm)。9个裂隙模型采用了相同的制作工艺,而且同时逐层制作,确保各层之间和各模型的制作质量一致。
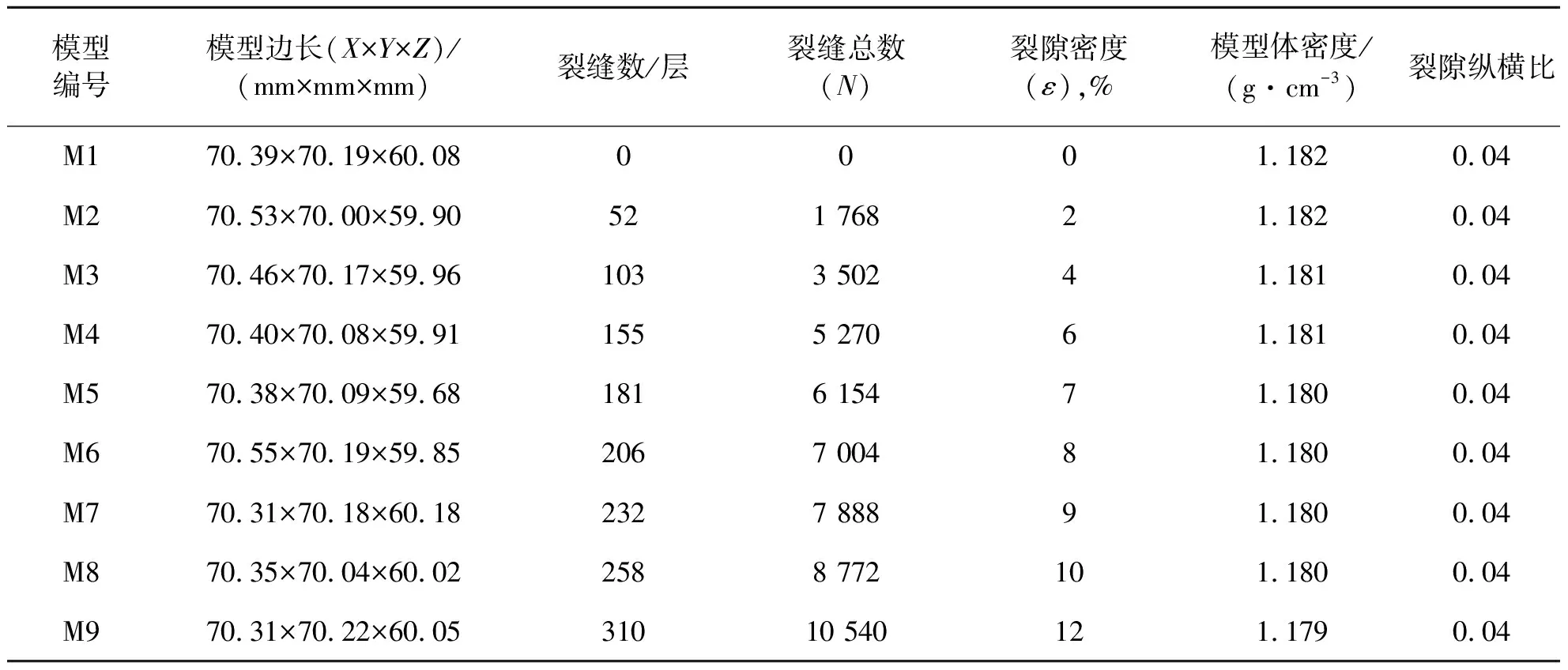
表1 裂隙密度模型尺度和裂隙参数模型

图2 裂隙模型中代表裂隙的薄币型圆片(a)和圆片厚度分布曲线(b)
1.2 裂隙模型横波速度测试
裂隙模型的横波速度测试在图3所示的测试系统上进行。测试系统由5077PR脉冲发/接收器、TK-DPO3102数字示波器、PC机和三种频率(谐振频率分别为0.50,0.25,0.10MHz)的宽频带横波换能器组成。不同的测试频率可以体现横波在裂隙模型中的波长变化。把激发和接收横波换能器放置在模型X(平行裂隙)或Z(垂直裂隙)方向的两个相对的外表面上,测试时激发和接收横波脉冲信号的换能器排在同一轴线上,且激发和接收换能器的偏振方向保持一致。通过测试超声波在模型中传播的距离L(X或Z)和时间(t),通过公式v=L/t计算速度。当横波平行裂隙(X轴)方向传播时,可测得偏振平行于和垂直于裂隙方向的两个横波速度(快横波vXY和慢横波vXZ);当横波垂直裂隙(Z轴)方向传播时,因为此方向是裂隙模型的对称轴,两个垂直偏振的速度(vZX和vZY)相同,取其平均值用vZX表示。
横波速度测试系统的精度将受耦合剂、横波换能器的纵振动和波形识别等因素的影响。本实验采用以下措施确保获得较高的测试精度:①使用特制蜂蜜作耦合剂可得到最佳的耦合效果,换能器与模型间经磨合加压后可获得均匀稳定的耦合层(小于0.1mm),此层的传播时间可以忽略;②选择固定的波形起跳点,以基质模型的波至作参考,选择第一周期负极性(波形向下)起跳点作波至时间;③采用数字示波器中的波形叠加测试功能,每次测试时选用16次叠加后拾取波至时间;④多次测试,对每个测试点分别进行3次(不同时间)测试,最后计算平均速度。所有实验记录的采样率都用0.1μs,经16次平均叠加后测试光标仅有一个采样点的误差。测试频率影响起跳点的读数误差,在0.50MHz时最大2个采样点,在0.25MHz和0.10MHz时有3~4个的采样点读数误差。因此,在本次实验中最大有±0.2μs的测试误差,速度误差为±3m/s。

图3 裂隙模型的横波速度测试系统
在无负载状态下3种频率的横波换能器的对零(t0)时间相同,当裂隙密度模型的传播距离相近时,从波形记录道上的传播时间观测到不同裂隙密度对横波的影响。
2 裂隙模型横波测试结果
2.1 快、慢横波波形特征
图4至图6是对9个裂隙模型用3种频率的横波换能器分别观测到的X方向(平行裂隙)的快、慢横波记录和Z方向(垂直裂隙)的慢横波记录。每张记录上的道数按裂隙密度大小(亦即模型序号)排序,第一道为无裂隙M1模型(ε=0)的记录,最后一道为最大裂隙密度M9模型(ε=12%)的记录。从图4中的每张记录中可以见到,横波初至信号之前都出现一些弱信号,这是横波换能器中纵振动模式引起的,这些信号振幅较小,且与横波信号的时差较大,对横波的波至没有影响。
图4给出了在裂隙密度模型X方向上观测的快横波(S1)记录。3种频率测试记录中的横波信号都很清晰,可以正确拾取横波到达时间。在无裂隙模型中,横波波至起跳点出现在57.25μs(图4a) 处;随着裂隙密度增大,快横波波至时间略有延迟,振幅下降。当测试频率降低时,快横波波至时间随着裂隙密度的变化更明显,振幅的影响则减小。
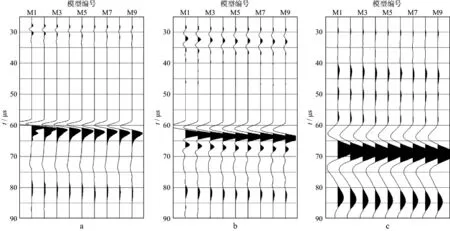
图4 在裂隙模型X方向上观测的0.50MHz(a),0.25MHz(b)和0.10MHz(c)频率下快横波记录
图5显示在裂隙密度模型X方向上观测的横波偏振垂直裂隙走向的3种频率慢横波记录。随着裂隙密度增大,慢横波的传播时间有明显的延迟,波形振幅下降,周期拉长。值得注意的是在0.50MHz频率测试记录(图5a)中,在横波波至前出现了一个正极性的小波包,且随着裂隙密度的增加此波包振幅增大和周期增多(见图5a中椭圆圈内所示)。在频率0.25MHz记录(图5b)中,此波包从裂隙密度6%(第4道)时开始出现(图5b中椭圆圈内所示),而在频率0.10MHz记录(图5c) 中未出现这种波包。显然,此波包与裂隙密度和测试频率相关,它的出现影响着对慢横波波至的拾取。
图6给出了在裂隙密度模型Z方向(垂直裂隙走向)观测的横波偏振平行X方向的三种频率慢横波记录。对比图5和图6,无裂隙模型上Z和X方向的波形特征除传播时间外完全一致,表明3种频率的测试条件基本相同。在图6记录中,随着裂隙密度的增加,波至时间延时的趋势与图5慢横波波至几乎一致,但在0.50MHz(图6a)和0.25MHz(图6b)频率的记录上未见到小波包;随裂隙密度增加图6中波形振幅下降比图5明显。
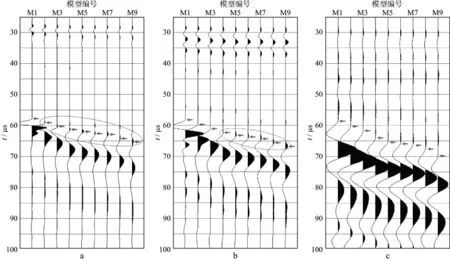
图5 在裂隙模型X方向上观测的0.50MHz(a),0.25MHz(b)和0.10MHz(c)频率下慢横波记录

图6 在裂隙模型Z方向上观测的X方向偏振的0.50MHz(a),0.25MHz(b)和0.10MHz(c)频率下慢横波记录
2.2 快、慢横波速度
模型测试的横波速度精度取决于对波至起跳点的拾取。在图4和图6记录中,横波波至时间很清晰,时间拾取误差小于0.5%。图5a和图5b中横波波至前出现的小波包是一种干扰波,对波至时间的拾取有较大影响。经反复测试分析认为,当慢横波前出现干扰波包时,以紧邻波至第一谷(或峰)的波包峰值位置作为慢横波的波至起跳点(见图5中箭头所指),此时的测试误差最小,约为0.8%。
表2给出了9个裂隙密度模型在3种频率下测试得到的快、慢横波速度。对无裂隙模型(M1)3种频率测得的速度在每种测试频率时几乎一致,表明层状的无裂隙模型是各向同性介质;随着测试频率的降低,横波速度约有1%的减小(大于测试误差),表明基质材料速度与测试频率有关,是一种由衰减引起的频散现象,这种现象在其它模型中同样存在,在后面对速度与频率关系的讨论中将对此进行分析。
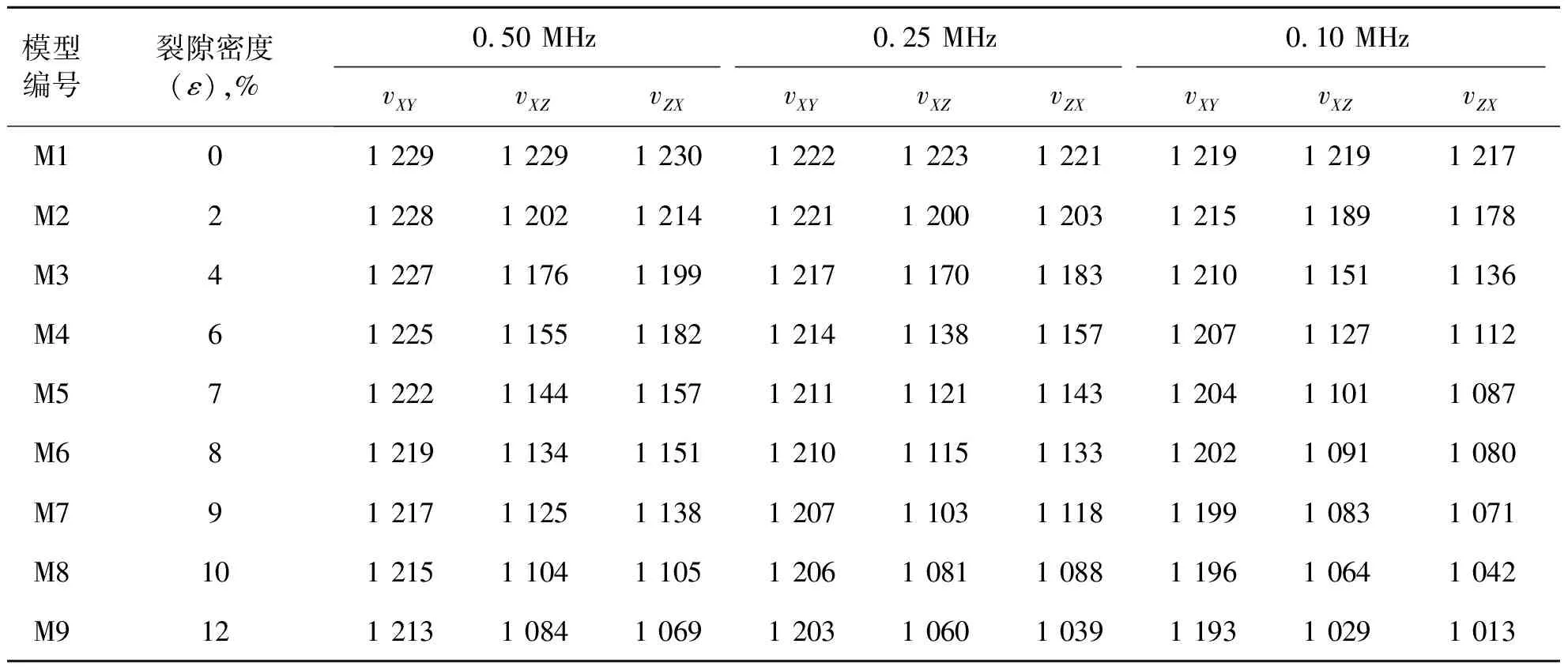
表2 3种频率下测得的裂隙密度模型横波速度 单位:m/s
由表2可见,裂隙密度从0增加到12%时,平行裂隙方向传播的快横波速度(vXY)下降1.3%(0.50MHz)到2.1%(0.10MHz);平行裂隙方向(X)上传播的慢横波速度(vXZ)随裂隙密度的增加下降明显,在11.8%(0.50MHz)到15.6%(0.10MHz)之间;垂直裂隙方向传播的慢横波速度(vZX)下降比平行裂隙方向的慢横波更多,达13.1%(0.50MHz)到16.8%(0.10MHz)。
原则上,定向排列裂隙介质可看作为横向各向同性介质,垂直裂隙方向的慢横波速度(vZX)与平行裂隙方向上的慢横波(vXZ)相同。在表2中看到,两者约有1%~2%的偏差。而且,当测试频率为0.50MHz和0.25MHz时,vZX>vXZ,最大差27m/s;测试频率为0.1MHz时,则vZX (1) 式中:vsh(90°)和vsh(0)分别表示平行和垂直的快横波和慢横波。弹性分量的一阶修正[13]: (4) 二阶修正: (5) 其中, 裂隙密度ε=N/Vr3。 对于“弱”裂隙充填物 (6) 其中 (4)式至(6)式中的λ,μ和k′,μ′分别为基质模型和裂隙薄片的拉梅系数,可由基质和裂隙充填物的纵、横波速度和密度得到。 表1和表2中给出了裂隙密度模型的裂隙密度和裂隙纵横比参数,以及基质(无裂隙模型)的横波速度,用3种频率测试测得基质的纵波速度分别为2647,2639,2623m/s,测得的裂隙圆片(块)的纵波速度分别为1360,1346,1334m/s,由此可计算出3种频率下的裂隙密度模型平行和垂直裂隙方向的快、慢横波速度。图7给出了裂隙密度模型实际测量和理论计算(虚线)的快、慢横波速度随裂隙密度变化曲线。由图7可以看到,无论是一阶修正后(红色短划线)或是二阶修正后(黑色虚线)的理论预测横波速度,都随裂隙密度的增加而增高。快横波速度(vXY)的理论计算一阶和二阶修正后的值几乎一致,慢横波速度(vXZ)的二阶修正后大于一阶修正后的值,这是因为在二阶修正中考虑了裂隙间的相互影响。 图7中用点的形式给出了表2实验测试值(实心点)和理论计算值(空心点)的对比。随着裂隙密度的增加,实测的横波速度下降趋势与理论计算值基本一致,最大偏差不超过5.0%。在3张不同测试频率的图上,随着频率的降低,实测快、慢横波速度减小量比理论值大,且与理论值间的偏差规律不同。快横波速度值在0.50MHz测试频率时大于理论值约1.5%,随频率降低两者偏差减小,在0.10MHz频率时实测值与理论值几乎一致。在0.50MHz和0.25MHz频率时,平行裂隙方向的实测慢横波速度(vXZ)分别与理论计算的一阶和二阶修正后的值几乎一致;0.10MHz频率时,小于理论值2.8%。 图7 裂隙模型在0.50MHz(a),0.25MHz(b)和0.10MHz(c)测试频率时的横波速度实测值和理论计算值 垂直裂隙方向的慢横波速度(vZX)与理论值(vZX=vXZ)的偏差稍大,在0.50MHz频率,大于一阶修正理论值约2.5%;在0.10MHz频率时小于理论值4.5%;在0.25MHz频率时实测的慢横波速度基本与理论值一致,偏差小于1.0%。 综合分析3种测试频率的快、慢横波速度实测值与相应的理论计算值随裂隙密度的变化规律可发现,0.25MHz频率测试值与Hudson理论计算值的偏差最小;在裂隙密度小于10%时最大偏差小于±1%。 由图7中见到,无论实测值或理论计算值,快、慢横波速度随裂隙密度的增加而减小,由于裂隙密度增大,模型内软物质增多,降低了整体的剪切模量。当横波平行裂隙传播,且振动方向也与裂隙平行时,裂缝面对波的传播和振动的影响较小,速度仅有稍微的降低;当传播方向或是振动方向与裂隙面垂直时,裂隙面较大程度地阻碍波能量的传递,慢横波的速度变化较大。 理论计算值中平行裂隙传播的慢横波与垂直传播的慢横波速度相同,因为理论模型给出的是一种等效的TI介质,在波长远大于裂隙尺度时具有较好的对称性。在实验中这种假设并不严格成立,两种不同方向的慢横波速度会因波长与裂隙尺度变化出现不同。0.50MHz和0.25MHz测试频率时横波波长约为2.44~4.88mm,与裂隙最大尺寸相近。裂隙作为一种尺度效应,vZX>vXZ表明裂隙面对振动影响大于传播方向的影响。0.10MHz测试频率时波长大于12.20mm,大于裂隙宽度的4倍,基本满足长波长条件,振动与传播方向的影响基本相同,所以表2中0.10MHz频率的2种实测慢横波速度值偏差最小。这表明平行和垂直裂隙方向的慢横波速度的差异与波长和裂隙尺度之比有关,比值接近1时,偏振因素影响大;比值大于1时,传播方向的散射影响大。 Hudson理论中的二阶修正主要是考虑了裂隙间的相互影响,图7中的理论计算曲线表明,二阶修正反而提高了裂隙介质的横波速度计算值。在实验中,裂隙间的相互影响主要出现在高频测试的慢横波中。此时裂隙尺度与波长相近,当横波偏振垂直裂隙面传播时,裂隙面随振动弯曲使慢横波质点振动并非严格地垂直于裂隙面,有部分振动分量甚至会平行于裂隙面,从而在慢横波初至前出现较快传播的干扰波包(图5a和图5b),形成速度快于慢横波的伴生波。裂隙密度增大时,裂隙横向的间距减小,即裂隙面增大,平行裂隙面振动的分量相应增多,伴生波能量适当增大。只有当波长大于裂隙面尺度较多时伴生波才消失。这与Hudson理论中二阶修正的机理不同。另一方面,慢横波初至前干扰波包的相位与慢横波相反且频率较高,从图5a中的各记录道可以发现,随着裂隙密度的增大,干扰波包的周期数增多,但振幅并不增大。这些现象都不符合慢横波的传播特征。慢横波初至前出现的波包对速度的测试精度有影响,反复测试表明有波包干扰时的测试精度降低0.4%~0.6%。 图8给出了快、慢横波速度在3种测试频率时随裂隙密度变化的曲线,显示了裂隙密度引起的频散现象。对于快横波速度由裂隙密度引起的频率影响较小,慢横波速度影响较明显,表明裂隙是一种方向性较强的散射体,慢横波的频散远大于快横波,所以引起了横波各向异性的速度频散。同时,由图7也可以看到,随着测试频率降低,快、慢横波速度测试值在理论计算值附近由高向低变化,这个现象符合速度频散规律。 图8 实测快横波速度(a)、平行裂隙方向传播的慢横波速度(b)和垂直裂隙方向传播的慢横波速度(c)在3种测试频率时随裂隙密度的变化 Hudson理论中的裂隙模型假设裂隙相互隔离,裂隙间流体不能流动,这种假设仅适合于模拟超高频率下饱和岩石属性,即适合于实验室超声频率测试条件[13]。由图7可知0.10MHz频率的实测快横波速度和0.25MHz的实测慢横波速度值几乎与理论计算值一致,尤其是慢横波速度,测试频率高于0.25MHz时实测值大于理论值,低于0.25MHz时实测值则小于理论值。说明Hudson理论对慢横波速度估算的频率限制在0.25MHz附近。同样,对于快横波速度估算的频率限制则在0.10MHz附近。 随测试频率降低,实测快、慢横波速度与理论值相符性有一些差异,这种差异可能是裂隙在Z方向等间隔分布引起的,当频率较高时平行裂隙面方向偏振的横波在裂隙间隔层内传播更有利,无论传播方向或是偏振方向垂直于裂隙面的慢横波,其速度是裂隙层和裂隙间隔层的综合效应。 在实验室通过低速度薄币圆片嵌入均质材料的方法构建了一组不同裂隙密度的物理模型,裂隙密度模型的基本参数与Hudson理论假设条件基本相符,用三种超声频率观测了此组模型在平行和垂直裂隙方向传播的横波速度,并与Hudson理论估算值进行了对比。当裂隙密度从0增加到12%时,实测值与理论计算值基本相符,与一阶修正结果最大偏差为4.5%。用不同频率测试时观测到明显的频散现象,且实测快、慢横波速度与理论值偏差随裂隙密度变化的规律不同。总体上,实测速度值随频率降低而减小,3种频率的实测快横波速度均高于理论估算值,频率下降至0.10MHz时实测值与理论值基本相符;实测慢横波速度随频率下降,从高于理论估算值变化到低于理论估算值,在0.25MHz时与理论值基本一致。实验结果表明,Hudson理论对快、慢横波速度的估算较适用于低频0.10~0.25MHz的测试值。在实验测试值中,偏振垂直裂隙方向时的横波速度与垂直裂隙方向时的横波速度有达2%的差异。在本实验中认为这与波长和裂隙尺度之比有关,比值接近1时,偏振因素影响大;比值大于1时,传播方向的散射影响大。 参 考 文 献 [1] Crampin S.A review of wave motion in anisotropic and cracked elastic-media[J].Wave Motion,1981,3(4):343-391 [2] Crampin S,Yedlin M.Shear-wave singularities of wave propagation in anisotropic media[J].Journal of Geophysics,1981,49(1):43-46 [3] Li X Y.Fractured reservoir delineation using multi-component seismic data[J].Geophysical Prospecting,1997,45(1):39-64 [4] Hudson J A.Overall properties of a cracked solid[J].Mathematical Proceedings of the Cambridge Philosophical Society,1980,88(2):371-384 [5] Hudson J A.Wave speeds and attenuation of elastic waves in material containing cracks[J].Geophysical Journal of the Royal Astronomical Society,1981,64(1):133-150 [6] Ass’ad J M,Tatham R H,Mcdonald J A.A physical model study of microcrack-induced anisotropy[J].Geophysics,1992,57(12):1562-1570 [7] Ass’ad J,Tatham R,Mcdonald J,et al.A physical model study of scattering of waves by aligned cracks:Comparison between experiment and theory[J].Geophysical Prospecting,1993,41(3):323-339 [8] Ass’ad J,McDonald J A,Tatham R H,et al.Elastic wave propagation in a medium containing oriented inclusions with a changing aspect ratio:a physical model study[J].Geophysical Journal International,1996,125(1):163-173 [9] Wei J X,Di B R,Wang Q.Experimental study on the effect of fracture scale on seismic wave characteristics[J].Petroleum Science,2008,5(2):119-125 [10] Wei J X.A physical model study of different crack densities[J].Journal of Geophysics Engineering,2004,1(1):70-76 [11] Rathore J S,Fjaer E,Holt R M,et al.P- and S-wave anisotropy of a synthetic sandstone with controlled crack geometry[J].Geophysical Prospecting,1995,43(6):711-728 [12] 魏建新,狄帮让.裂隙密度对纵波传播特性影响的实验观测[J].石油地球物理勘探,2007,42(5):554-559 Wei J X,Di B R.Experimentally surveying influence of fractural density on P-wave propagating characters[J].Oil Geophysical Prospecting,2007,42(5):554-559 [13] Mavko G,Mukerji T,Dvorkin J.The rock physics handbook:tools for seismic analysis of porous media[M].New York:Cambridge University Press,2009,1-3293 横波速度理论估算值与实验值对比


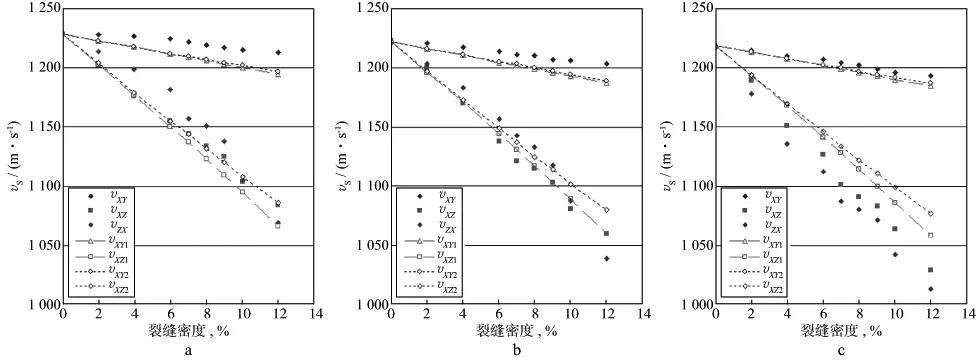
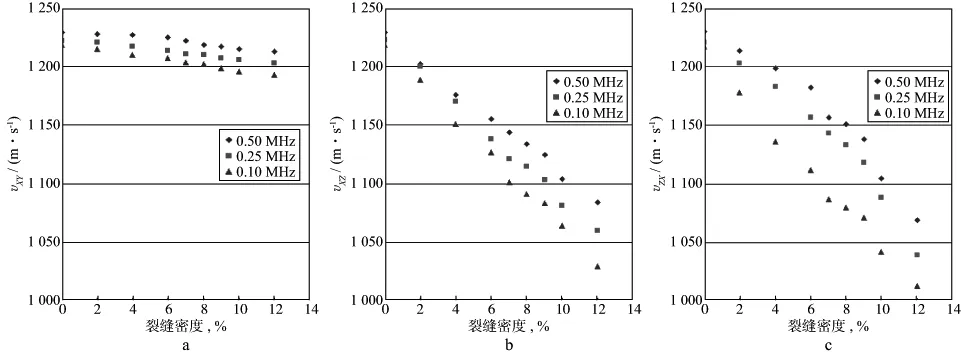
4 结果分析
5 结束语

