基于反演策略的数据自适应衰减补偿方法

王本锋,陈小宏,李景叶,陈增保

(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京102249;2.中国石油大学(北京)海洋石油勘探国家工程实验室,北京102249)

由于地下介质的非均匀性以及黏滞性对地震波产生了吸收衰减作用(即正Q滤波效应),使其振幅减弱、相位畸变,地震记录的分辨率降低[1]。Varela等[2]利用Futterman衰减频散关系分析了衰减与频散效应,验证了地下介质的吸收衰减效应。衰减补偿是提高地震记录分辨率,进行精细油藏描述的有效途径之一[3]。反Q滤波是衰减补偿的重要方法,其相位校正无条件稳定且具有较强的抗噪性,但振幅补偿因子随着传播时间的增大以及频率的增加呈指数放大趋势,稳定性及抗噪性较差[4-7]。Hargreaves等[8]利用类似Stolt频率-波数域偏移的方法,高效地实现了反Q滤波算法,有效地校正了由速度频散引起的相位畸变,但为了避免振幅补偿的不稳定性,仅对相位进行了校正。赵建勋等[9]通过反Q滤波与串联偏移相结合,将常Q算法推广至深变Q值模型；通过串联频散补偿算法与限幅补偿算法相结合,更好地提高了地震记录的分辨率。

针对反Q滤波振幅补偿的不稳定性,Wang[4,6]提出了振幅增益控制方法以及稳定的反Q滤波方法(可同时补偿振幅以及校正相位),设计了Gabor域算法以提高计算效率。对含噪地震记录,振幅增益控制方法在提高分辨率的同时,较大地放大了噪声,导致振幅补偿不稳定;稳定的反Q滤波方法可较好地处理含噪地震记录,但一定程度上导致振幅欠补偿。Yan等[10]将稳定的反Q滤波公式推广至多分量地震勘探中,利用叠前转换波道集提取S波的Q值,利用叠前纵波道集提取P波的Q值,实现了叠前PP波以及PS波的衰减补偿,提高了叠前地震记录的分辨率。Zhao等[11]为克服振幅补偿过程中噪声被放大的缺陷,在时频域定义信噪比,对信噪比大于1的区域进行振幅补偿,其它区域不进行补偿,从而在保证信噪比的前提下,提高了地震记录的分辨率。为减弱反Q滤波对Q值的依赖性,Braga等[12]在小波域实现反Q滤波方法,在Q值误差较大时,补偿后的地震记录能在提高分辨率的同时依然保持原有的AVO特性,从而有利于叠前反演。Zhang等[13]为克服反Q滤波振幅补偿不稳定或欠补偿的缺陷,利用最小二乘策略以及贝叶斯理论,给定子波或提取最小相位子波来迭代反演稀疏的反射系数序列,提取Q值作相位校正,得到高分辨率的地震记录。Wang[14]利用Futterman吸收衰减模型,基于爆炸反射面模型推导了正Q滤波公式,利用正则化策略以及反演理论反演得到补偿后的地震记录,克服了常规反Q滤波方法振幅补偿不稳定或欠补偿的缺陷,且具有一定的抗噪性。Margrave等[15]将维纳反褶积进行推广,提出Gabor反褶积策略;Margrave等[16]在Q值未知以及反射系数白噪的前提下,对衰减地震记录的Gabor谱进行双曲平滑,统计衰减函数以及最小相位子波,最终得到高分辨率的反射系数序列。Reine等[17]基于窗口变化与否分析了时频分析方法度量地震波衰减的稳健性,提出变窗口的时频变换方法可降低衰减估计的不确定性以及估计偏差,使其具有较高的精度,但该时频分析方法均假设子波是最小相位的,一定程度上偏离实际情况。

我们借鉴反Q滤波思想仅进行吸收衰减补偿,在Gabor域基于能量均分双曲平滑方法估计衰减函数谱,基于非稳态褶积理论[18],利用正则化方法反演得到衰减补偿后的高分辨率地震记录。

2 方法原理

2.1 非稳态褶积理论

假设震源子波为w(t),反射系数序列为r(t),根据褶积原理,理想的无噪声地震记录s(t)的表述为

(1)

由于地下介质的非均匀性以及黏滞性,地震子波在传播过程中被吸收、衰减产生频散效应,实际上为非稳态子波,因此基于稳态褶积的处理结果往往偏离实际情况[16]。Margrave[18]将稳态褶积模型推广到非稳态褶积情况,公式为

(2)

根据Gabor变换的性质知

(3)

其中,S(f,τ),R(f,τ),α(f,τ),W(f)分别为衰减地震记录以及反射系数的Gabor谱、衰减函数、稳态子波频谱。在时频域,可以较容易地估计出非稳态子波的振幅谱,并在最小相位的假设下,借助希尔伯特变换求得相位谱,从而实现非稳态反褶积。因此将非稳态褶积公式(2)转换到时频域:

(4)

其中,S(f)为衰减记录的频谱,αw(f,τ)为衰减子波的时频谱。

由于实际子波大多为混合相位子波,基于最小相位子波假设的非稳态反褶积方法一定程度上偏离实际情况,因此我们忽略子波的影响,仅消除吸收衰减的效应,提高地震记录的分辨率。非稳态褶积公式(4)演变为

(5)

其中,α(f,τ)为复值衰减函数,s0(τ)是原始未衰减的地震记录。

公式(5)可离散成矩阵方程组的形式,即

(6)

其中,S为包含地震数据带限频率成分的复值向量,Φ为含有衰减以及傅里叶变换信息的复值矩阵,s0为原始未衰减记录(补偿后记录),为一实值向量。

将公式(6)转换为实值方程,即

(7)

(8)

其中,μ为正则化因子,D为微分算子,可选为单位算子、一阶微分算子或二阶微分算子。

将(8)式分别对s0求导并令之为0,即可获得关于s0的正则化方程:

(9)

可利用共轭梯度算法、牛顿法等对正则化方程进行求解,最终得到衰减补偿后的地震记录。但是复值衰减函数α(f,τ)一般是未知的,如何得到精确的衰减函数,成为衰减补偿的关键问题。

2.2 衰减函数估计

衰减函数的理论表达式为

(10)

其中,Q为品质因子,H(·)为沿频率方向的希尔伯特变换,其假设衰减函数为最小相位。如果已知Q值,则衰减函数具有解析表达式。但是精确的Q值估计相对困难且其误差会影响衰减补偿的精度,导致错误的解释结果。因此,避开Q值估计问题,直接估计衰减函数可提高补偿精度。令c=τf,根据衰减函数的理论表达式知,在c等值线上衰减值相同,因此在反射系数白噪的假设前提下,对衰减地震记录的Gabor谱进行双曲平滑可估计衰减函数的振幅谱;在最小相位假设下,利用希尔伯特变换可求得相应的相位谱,利用公式(9)反演得到衰减补偿后的地震记录。

不同的双曲平滑方法对衰减函数的估计精度不同。传统的双曲平滑方法[16]将时频域分成N个双曲型条带,条带边界为ci=(i-1)dc,i=2,…,N+1,c1=0,dc=cmax/N,如图1所示。

图1 传统双曲平滑方法条带分割a N=10; b N=30

由图1a可知,传统的双曲平滑分割方法对c值较小的区域欠采样，对c值较大的区域过采样,而地震信号的主要能量集中在c值较小的区域,使得估计的衰减函数谱精度较低。增加划分条带的数目,如图1b所示,一定程度上可提高估计精度,但是光滑方法属于统计方法,条带数目增多,则每一条带内的样点数减少,统计效应减弱。

另外,以ci=exp[(i-1)dc],i=2,…,N+1,c1=0为条带边界,也可将时频域分成N个双曲型条带,如图2所示,其中dc=(lncmax)/N。得到的双曲型条带宽度从低c值到高c值逐渐增加,克服了传统双曲光滑方法在c值较小区域的欠采样问题。c值较大区域的过采样问题也得到了一定程度上的缓解，但是位于低c值条带内的样点数减少,统计效应减弱,且其只是运用数学方法机械地将条带宽度进行调整,缺乏物理涵义。

图2 对数域双曲平滑方法条带分割a N=10; b N=30

针对双曲平滑方法遇到的问题,Li等[19]基于能量均分思想,提出变步长的双曲平滑方法。由理论衰减函数振幅谱A=exp(-πτf/Q)=exp(-πc/Q)知,c在[0,cmax]变化时,A的取值范围为(0,1],将能量区间进行均分，即dA=1/N,得到条带边界ci=-{ln[(i-1)dA]}Q/π,c1=0。品质因子Q未知,但由于平滑得到的估计值对Q值不敏感,所以Q取经验常数值即可。能量均分双曲平滑分割方法具有一定的物理涵义,其按照能量进行区域分割与叠前反演抽取近、中、远偏移距道集类似。图3展示了分割份数N=10,30时分别对应的c条带分割结果。分割份数较少时,如图3a所示,在保持统计效应的同时,克服了c值较小的区域欠采样以及c值较大的区域过采样问题。

图3 能量平滑双曲平滑方法条带分割a N=10; b N=30

将时频域分割成N个双曲型条带之后,在每一条带内估计均值Ek,并将该平均值放置在双曲条带的中心线mk上:Ek=mean({|S(τ,f)|,(τ,f)∈Ωk}),其中Ωk为第k个双曲型条带,mk=0.5×(ck+ck+1)。

假设时频域(τ,f)点位于[mk,mk+1],其中mk为第k个条带的中心,由双曲平滑方法得其时频谱值Ek,则(τ,f)点处的时频谱值可由插值方法获得，即

(11)

3 数值模型算例与实际资料处理

本文方法为单道处理方法,为验证方法的可行性，首先设计反射系数序列,分别与最小相位以及零相位子波褶积合成无衰减的地震记录,利用非稳态褶积理论合成衰减的地震记录；然后基于传统双曲平滑以及能量均分双曲平滑方法进行衰减函数估计,利用反演策略进行衰减补偿。通过对实际资料进行处理,验证了方法的有效性。

3.1 理论模型分析

设计的反射系数序列如图4a所示;零相位子波为30Hz的雷克子波,如图4b所示;最小相位子波为与零相位子波振幅谱相对应的最小相位子波,如图4c所示。

基于褶积理论以及非稳态褶积理论(品质因子Q=50)的最小相位子波合成记录、零相位子波合成记录及其理论衰减函数谱分别如图5，图6和图7 所示。由图5b，图6b可知,随着传播时间的增加,子波的能量逐渐减弱,且高频损失相对严重;由图7可知,随着时间的增加和频率的提高,衰减量越来越大。

图4 反射系数序列(a)与零相位子波(b)以及最小相位子波(c)

对最小相位子波合成的未衰减以及衰减地震记录(图5)进行Gabor谱分析,如图8所示。由图8a 可知,未衰减地震记录Gabor谱的深、浅层能量相对均衡,由于带限子波的影响,能量主要集中在中、低频区域;由图8b可知,衰减地震记录的Gabor谱能量随着传播时间的增加逐渐减小,且高频成分衰减相对较快,与理论衰减规律一致。

图5 衰减前(a)、后(b)的最小相位子波合成记录

图6 衰减前(a)、后(b)的零相位子波合成记录

图7 理论衰减函数谱

图8 最小相位子波合成的未衰减记录Gabor谱(a)以及衰减记录Gabor谱(b)

基于传统的双曲平滑方法,将时频区域分割成N=10,30,50,100份得到的衰减函数谱如图9a至图9d所示。可以看出,随着分割份数的增加,估计得到的衰减谱与理论衰减谱(图7)越来越接近;但是条带数越多,每个条带内的采样点越少,统计效应越弱。基于能量均分的双曲平滑方法(N=10)估计得到的衰减谱如图10所示,该方法在分割份数较少的情况下与理论衰减模型(图7)具有较好的一致性,在保持统计性的同时,具有较高的精度。由估计的衰减函数振幅谱在最小相位假设下利用希尔伯特变换得到相位谱,基于公式(9)反演得到补偿后的地震记录,如图11所示。

图9 传统双曲平滑方法不同分割份数估计的衰减谱a N=10; b N=30; c N=50; d N=100

图10 能量均分双曲平滑方法估计的衰减谱(N=10)

分析图9至图11可见,传统的双曲平滑方法估计的衰减谱的精度随着分割份数的增加而提高,基于该衰减谱反演得到的补偿记录的精度也相应提高;基于能量均分的双曲平滑方法在分割份数较少、保证统计性的前提下,估计得到的衰减谱(图10)与理论衰减谱(图7)具有较高的一致性,利用该衰减谱反演得到的补偿后的地震记录(图11g)与未衰减地震记录(图11a)具有较高的一致性。综合分析可知,基于能量均分的双曲平滑方法相对传统的双曲平滑方法具有较大的优势,估计得到的衰减谱精度较高,反演得到的补偿后地震记录与原始未衰减记录具有较好的一致性。

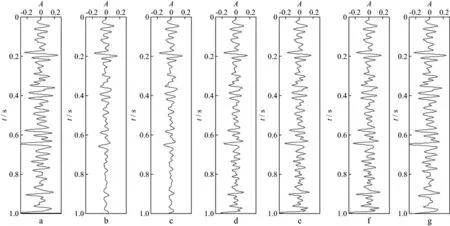
图11 理论模型数据衰减补偿前后的地震记录a 原始未衰减地震道; b 品质因子Q=50时的衰减记录; c—f 基于传统双曲平滑方法在分割份数分别为10，30，50，100时估计的衰减谱反演得到的补偿后地震记录; g 基于能量均分双曲平滑方法估计的衰减谱反演得到的补偿后地震记录

将能量均分双曲平滑方法以及反演策略应用于零相位子波合成的地震记录(图6)中,处理过程与处理最小相位子波合成记录类似,补偿后的地震记录如图12所示。由图12可见,基于能量均分双曲平滑方法以及反演策略得到的补偿地震记录与原始未衰减地震记录具有较好的一致性,补偿的精度较高。理论模型数据试算的结果表明，我们研究并提出的方法对地震子波的相位没有特殊要求,且不需要精确Q值的信息,衰减函数从地震记录的Gabor谱中统计得到,利用反演的策略得到衰减补偿后的地震数据避免了振幅补偿的不稳定性,实现了提高地震记录分辨率的目的。由于忽略子波的影响,该方法具有数据自适应性。

3.2 实际地震资料处理

图13a为某油田实际叠后地震资料,共有251道,每道651个采样点,时间采样率为2ms。可以看出,由于吸收衰减作用,深层地震反射同相轴能量相对较弱,波形畸变且连续性较差(黑色椭圆以及箭头所示位置)。利用本文方法,首先从地震记录的Gabor谱中估计衰减函数谱,在衰减函数最小相位的假设下,利用希尔伯特变换求得相位谱,利用公式(9)实现地震记录的衰减补偿。补偿后的地震剖面如图13b所示,深层反射能量相对增强,波形得到一定程度的校正,且连续性变好,剖面分辨率得到提高。实际地震资料处理验证了本文方法的有效性。

图12 零相位子波合成记录以及补偿结果a 原始地震记录; b Q=50对应的衰减地震记录; c 补偿后的地震记录

图13 实际地震资料衰减补偿前(a)、后(b)的剖面对比

4 结论与认识

我们基于非稳态地震道模型,利用能量均分双曲平滑方法从衰减地震记录的Gabor谱中估计衰减函数,基于反演策略得到补偿后的地震数据。研究得出以下几点结论与认识:

1) 该方法忽略子波的影响,对子波的相位无要求,适用于任意相位子波合成的地震记录,克服了Gabor反褶积中子波最小相位假设的缺陷;

2) 该方法不需要精确的Q值信息,衰减信息从观测地震记录的Gabor谱中提取,克服了常规反Q滤波需要精确Q值的弊端;

3) 该方法基于反演思想得到补偿后的地震数据,避免了常规反Q滤波振幅补偿的不稳定性;

4) 相对传统双曲平滑方法，基于能量均分双曲平滑方法估计衰减谱的精度高,据此反演得到的衰减补偿记录分辨率更高;

5) 该方法没有消除子波的影响,建议对补偿后的地震记录进行稳态盲反褶积处理,同时得到子波信息以及高分辨率的反射系数序列;

6) 该方法为单道处理方法,没有考虑横向约束,有待拓展到多道处理,提高横向的连续性;

7) 基于衰减函数最小相位假设和利用希尔伯特变换求取相位谱时会带入计算误差,下一步需要研究如何减弱最小相位假设和提高精度。

参 考 文 献

[1] Futterman W I.Dispersive body waves[J].Journal of Geophysical Research,1962,67(13):5279-5291

[2] Varela C L,Rosa A L R,Ulrych T J.Modeling of attenuation and dispersion[J].Geophysics,1993,58(8):1167-1173

[3] Van der Baan M.Bandwidth enhancement:inverse Q filtering or time-varying Wiener deconvolution?[J].Geophysics,2012,77(4):V133-V142

[4] Wang Y.A stable and efficient approach of inverse Q filtering[J].Geophysics,2002,67(2):657-663

[5] Wang Y.Quantifying the effectiveness of stabilized inverse Q filtering[J].Geophysics,2003,68(1):337-345

[6] Wang Y.Inverse Q-filter for seismic resolution enhancement[J].Geophysics,2006,71(3):V51-V60

[7] Zhang X,Han L,Zhang F,et al.An inverse Q-filter algorithm based on stable wavefield continuation[J].Applied Geophysics,2007,4(4):263-270

[8] Hargreaves N,Calvert A.Inverse Q filtering by Fourier transform[J].Geophysics,1991,56(4):519-527

[9] 赵建勋,倪克森.串联反Q滤波及其应用[J].石油地球物理勘探,1992,27(6):722-730

Zhao J X,Ni K S.Cascaded inverse Q filtering and the application[J].Oil Geophysical Prospecting,1992,27(6):722-730

[10] Yan H,Liu Y.Estimation of Q and inverse Q filtering for prestack reflected PP- and converted PS-waves[J].Applied Geophysics,2009,6(1):59-69

[11] Zhao Y,Liu Y,Li X,et al.An approach of inverse Q filtering considering time-frequency domain signal-to-noise ratio[J].74th EAGE Conference & Exhibition,2012,P103

[12] Braga I L S,Moraes F S.High-resolution gathers by inverse Q filtering in the wavelet domain[J].Geophysics,2013,78(2):V53-V61

[13] Zhang C,Ulrych T J.Seismic absorption compensation:a least squares inverse scheme[J].Geophysics,2007,72(6):R109-R114

[14] Wang S.Attenuation compensation method based on inversion[J].Applied Geophysics,2011,8(2):150-157

[15] Margrave G F,Dong L,Gibson P,et al.Gabor deconvolution:extending Wiener’s method to nonstationarity[R].Calgary:CREWES Research Report,2003

[16] Margrave G F,Lamoureux M P,Henley D C.Gabor deconvolution:estimating reflectivity by nonstationary deconvolution of seismic data[J].Geophysics,2011,76(3):W15-W30

[17] Reine C,van der Baan M,Clark R.The robustness of seismic attenuation measurements using fixed-and variable-window time-frequency transforms[J].Geophysics,2009,74(2):WA123-WA135

[18] Margrave G F.Theory of nonstationary linear filtering in the Fourier domain with application to time-variant filtering[J].Geophysics,1998,63(1):244-259

[19] Li F,Wang S,Chen X.Gabor deconvolution-hyperbolic smoothing with variable -step sampling[J].75thEAGE Conference & Exhibition,2013,Th-06-04