基于三维曲波变换的地震数据去噪方法研究
孟阁阁,王德利,陈 鑫
(吉林大学地球探测科学与技术学院,吉林长春130026)
常规的地震资料去噪方法基于傅里叶变换[1],如频率域滤波法、F-K滤波法等。但作为全局变换的傅里叶变换对整个时域进行平均,丢失了时间信息,对实际信号中一些非平稳的奇异点或奇异曲线的时变局部特征描述不够准确。作为傅里叶变换的延伸与发展,学者们提出了F-X域反褶积滤波[2]和小波变换[3]等算法。但是,F-X域反褶积滤波算法会加强地震记录中的所有相干信息;而小波变换作为一种多尺度变换,虽然能够更稀疏地表示一维分段函数或有界变差函数,但对于高维信号的边缘信息表达能力存在局限性。因此,需要有一种更为稀疏的变换来表示地震反射层。
Candès等[4]于1999年首次提出第一代曲波变换,它是由脊波变换衍生而来的一种多尺度几何分析变换。曲波变换具有尺度、角度和位置分量,这使它不再仅仅局限于空间域和频率域,也能够在定向上实施,因此能够对于含有奇异点的二维信号达到几乎最优的稀疏表示。至2004年,Candès等[5-6]又提出了第二代曲波变换,第二代的二维曲波变换无需用到脊波变换,提高了曲波变换的实现速度。在2004年的SEG年会上,开始出现曲波变换被用于地震数据多次波衰减[7]及曲波域的叠前偏移[8]等应用研究论文。由于单独的二维曲波变换只能应用于单炮地震数据,为了使曲波变换也可以应用于多炮地震数据,Ying等[9]于2005年提出了三维离散曲波变换算法,为曲波变换用于分析和处理多炮数据和三维数据开启了新的途径。为了提高运算速度,减少计算过程中产生的冗余,Candès等[10]于2006年提出了两种快速离散曲波变换算法。在2007年的SEG年会上,Herrmann等[11]介绍了基于曲波变换的地震数据缺失道插值方法,并将其应用于理论模型和实际三维数据体。2008年,Ramesh等[12]论述了一种基于曲波变换的随机噪声压制方法。
在国内,随着人们对曲波变换认识的加深,曲波变换在地震数据处理中的应用也逐渐引起重视。张素芳等[13]于2006年将曲波变换应用于地震数据多次波消除;2008年,彭才等[14]给出了基于曲波变换的地震数据去噪方法;同年,王德利等[15]提出了一种基于曲波变换的稀疏控制反演方法;张恒磊等[16]于2010年将曲波变换应用于地震波场分离中。至2013年,曲波变换已先后被应用于稀疏反褶积[17]和地层吸收补偿[18]等问题中;冯飞等[19]还提出了基于三维曲波变换的稀疏反演一次波估计方法。总体来看,基于三维曲波变换的方法研究和应用研究在国内还处于起步阶段。
基于三维曲波变换良好的稀疏性,可以用更少的系数立体全面地重构地震反射信号,我们将三维曲波变换与阈值迭代法结合,将其应用于多炮地震数据的随机噪声压制中。在曲波域中用曲波系数描述地层反射系数,在稀疏条件下地震数据中随机噪声的衰减问题可以描述为L1范数最优化问题,对此用阈值迭代法进行求解,以达到压制随机噪声的目的。采用多炮理论模型数据和实际地震资料对基于三维曲波变换的阈值迭代去噪算法进行验证,并选用信噪比、保真度等评价参数与几种传统去噪方法的效果进行量化对比分析。
1 三维曲波变换的基本理论
曲波变换用“楔形基”代替小波变换的“块基”来逼近二次连续可微的奇异点,所以能够更好地描述沿边缘的信息。三维曲波变换[9]是二维曲波变换的延伸与扩展,在尺度、角度和位置分量上具有与二维曲波变换相同的性质。
在频率域中,二维曲波变换的支撑区域是一个“楔形”,三维曲波变换的频率支撑建立在具有抛物型尺度属性的楔形附近。连续三维曲波变换的基函数在频率域中以一个球体的形式逐渐分割覆盖(图1),径向上使用与二维曲波变换相同的窗口W(r):
(1)


图1 连续三维曲波变换分割示意图解[9]
离散三维曲波变换的基函数在频率域中以方块体的形式逐渐分割覆盖(图2)。类似于离散二维曲波变换,离散三维曲波变换输入的是三维笛卡尔网格形式f(n1,n2,n3),0≤n1,n2,n3≤n,输出曲波系数集cD(j,l,k):
(2)
其中,j,l∈Z,k=(k1,k2,k3)。
用笛卡尔半径的形式表示径向窗函数:
并且,φj(ω1,ω2,ω3)=φ(2-jω1)φ(2-jω2)φ(2-j·ω3)。其中,φ是低通圆滑函数;φ是曲波变换的“母波形”。
离散三维曲波变换的基函数分割体有6个面,在精细尺度下,以第1部分(ω1>0)为例:假设(1,αl,βl)是楔形中心线的方向,角窗口函数定义为
(5)
对于其它的5个部分,交换ω1与ω2或ω1与ω3来进行类似定义。
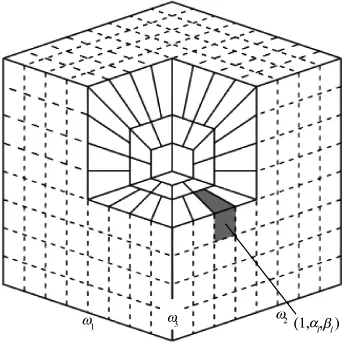
图2 离散三维曲波变换分割示意图解[9]

(6)
位移参数为k的离散曲波在尺度j和角度l上由它们傅里叶变换的方式给出
(7)
其中,0≤k1 离散三维曲波变换算法实现步骤如下。 一般的阈值去噪算法都分为信号分解、系数阈值处理、信号重构3个步骤,基于三维曲波变换的阈值迭代算法也不例外。曲波变换良好的稀疏性决定了它的优越性,如图3所示,将曲波变换的“楔形”基用长方形窗口近似代替,这种长方形窗口也体现了曲波基特有的方向性。图3中曲线表示地震反射层。小波变换(图3a)用类似正方形的窗口来描述地层曲线;而曲波变换(图3b)的窗口函数是类似于长方形的。对比图3a和图3b可以看出,小波变换需要较多的窗口才能描述地层,并且这种“正方形”窗口函数不具有方向性,而曲波变换只用少数的曲波系数就能很好地描述地层反射信号,“长方形”窗口函数的方向性使有效信号主要集中在沿曲线方向的曲波系数上,即小倾角的曲波系数上,而随机噪声在任何正交基上的变换仍然是随机地分布在整个空间上。一般来说噪声的曲波系数值由于能量分散且幅值较小而往往小于有效信号的曲波系数值,因此只要选择一个适当的阈值,对曲波系数进行阈值处理,就可以达到有效信号与噪声分离的目的。 图3 小波逼近(a)与曲波曲线逼近(b)示意图解 Daubechies等[20]给出了一种稀疏约束下的正则化方法的求解迭代序列: (8) 其中, (9) 稀疏约束情况下,Elad等[21]提出了地震数据中随机噪声的衰减可以简化表述为如下的约束优化公式: (10) 式中:y是待处理的含噪地震数据;λ为拉格朗日算子;A表示三维曲波逆变换;x表示曲波系数;f为最终输出结果。Pλ问题实际上是求解L1范数最优化的过程,我们采用软阈值迭代法对其进行求解。 根据(8)式可知其迭代序列为 (11) 式中:AT表示三维曲波正变换;Tλ为软阈值函数,其表达式为 (12) 获得良好去噪效果的关键是阈值的选取,我们根据以下两个公式来选取阈值: 三维曲波阈值迭代法去噪处理的步骤见图4 所示,图中i表示当前外循环次数;j表示当前内循环次数;L表示总的外循环次数;l表示总的内循环次数;x表示曲波系数。 图4 三维曲波阈值迭代法去噪处理流程 为了说明三维曲波变换较其它常规方法拥有更好的去噪效果和保真能力,先对模拟多炮地震数据进行测试。所用模拟数据有181炮,每炮有181道记录,共1125个采样点,采样间隔为0.0016s。在模拟原始数据中加入不同程度的随机噪声,针对高信噪比模拟数据和低信噪比模拟数据两种情况,分别采用传统中值滤波方法、F-X反褶积方法、二维曲波阈值迭代法和三维曲波阈值迭代法进行去噪处理。 图5a给出了模拟原始数据的第83炮原始记录;图5b是加噪后高信噪比模拟记录;图5c到图5f 分别给出了上述4种方法的去噪处理结果。 为了计算去噪后数据的信噪比和保真度,更好地对比不同方法的去噪效果,定义如下评价参数。 1) 信噪比: (15) 2) 峰值信噪比: 图5 模拟原始数据(a)和加噪后高信噪比数据(SNR=5.5691dB)(b)的中值滤波法(c),F-X反褶积法(d),二维曲波阈值迭代法(e)和三维曲波阈值迭代法(f)去噪处理结果 (16) 式中:s0表示原始无噪声数据;s1表示加噪声数据或去噪后数据;M代表数据的行数;N代表数据的列数。 3) 均方差: (17) 4) 平均绝对误差: (18) 式中:v0i为原始无噪数据;vi为去噪后数据。 5) 去噪能力: (19) 式中:SNR0为原始含噪数据的信噪比;Enoise为去噪后数据中的噪声能量;Enoise0为原始含噪数据中的噪声能量。 表1给出了对含噪高信噪比模拟数据利用4种方法去噪处理结果计算的信噪比SNR,峰值信噪比PSNR,均方差MSE,平均绝对误差MAE和去噪能力DA的对比。 由图5和表1可以看出,对于图5b所示信噪比较高的含噪模拟数据(SNR=5.5691dB;PSNR=33.3821dB),中值滤波法去噪结果(图5c)效果差强人意(SNR=5.9236dB;PSNR=33.73631dB), 有效信息损失严重(MSE=0.455×10-5)。F-X反褶积法去噪结果(图5d)由于有效信号与相干噪声同时加强,所以信噪比提高量不大(SNR=6.7077dB;PSNR=34.5207dB),保真效果也不太理想(MSE=0.3790×10-5)。二维曲波阈值迭代法取得了不错的去噪效果(SNR=13.5072dB;PSNR=41.3202dB;MSE=0.0790×10-5)(图5e),但是同相轴曲率较大处信息模糊。经三维曲波阈值迭代法去噪后(图5f),信噪比得到了显著提升(SNR=15.9672dB;PSNR=43.7801dB),同相轴连续、清晰,且有效信息损失也是最小的(MSE=0.0450×10-5),获得了满意的效果。 图6a和图6b分别为采用二维曲波阈值迭代法和三维曲波阈值迭代法去噪前、后的差值剖面,在图中箭头所示的位置可以明显地看出,经二维曲波阈值迭代去噪后的差值剖面上同相轴残余较多,而经三维曲波阈值迭代去噪后的差值剖面上有效信息明显减少。可见,三维曲波阈值迭代法不仅去噪效果好,而且有效信息的损失相对较小。 进一步对低信噪比模拟数据进行测试。为了便于比较,这里仍然针对其中的第83炮模拟原始记录(图7a)。图7b是加噪后的低信噪比模拟数据(SNR=-8.4118dB),分别采用中值滤波法(图7c),F-X反褶积法(图7d),二维曲波阈值迭代法(图7e)和三维曲波阈值迭代法(图7f)进行去噪处理。表2是对含噪低信噪比模拟数据利用4种方法去噪处理结果计算的信噪比SNR,峰值信噪比PSNR,均方差MSE,平均绝对误差MAE和去噪能力DA。 表1 高信噪比模拟数据4种方法去噪结果的评价参数 图6 高信噪比模拟数据二维曲波阈值迭代法(a)和三维曲波阈值迭代法(b)去噪前、后的差值剖面 图7 模拟原始数据(a)和加噪后低信噪比数据(SNR=-8.4118dB)(b)的中值滤波法(c),F-X反褶积法(d),二维曲波阈值迭代法(e)和三维曲波阈值迭代法(f)去噪处理结果 中值滤波 F-X反褶积二维曲波三维曲波SNR/dB-7.9800 0.4805 4.59218.3245PSNR/dB 19.8324 28.293532.4052 36.1375MSE 1.1170×10-4 0.1590×10-40.0620×10-4 0.0260×10-4MAE 0.7530×10-20.2780×10-20.1660×10-2 0.1100×10-2DA0.1560 1.61302.8080 3.6380 由图7和表2可以看出,对于含有较多随机噪声的地震数据(SNR=-8.4118dB;PSNR=19.4021dB),中值滤波法去噪的效果(图7c)不太理想,剖面中仍有大量的噪声(SNR=-7.980dB;PSNR=19.8324dB),并且有效信号损失较多(MSE=1.1170×10-4)。经F-X反褶积法去噪后(图7d),信噪比虽然有所提高(SNR=0.4805dB;PSNR=28.1935dB),但是有效信号信息明显减弱(MSE=0.1590×10-4)。二维曲波阈值迭代法结果(图7e)虽然去除了大量噪声(SNR=4.5921dB;PSNR=32.4052dB),剖面视觉效果优于图7c和图7d,但是从图7e中0.5~1.0s两个箭头处可以看出,二维曲波阈值迭代法在同相轴曲率较大处损失较大(MSE=0.0620×10-4),出现了假频;从图7e中1.5s上、下的两个箭头处可以看出,二维曲波阈值迭代法很难保证弱有效信号的真实信息,不利于后续数据处理工作的进行;从图7e 整体可以看出,随着信噪比的降低,二维曲波阈值迭代法去噪后的剖面背景中存在一些明显的小曲波分量,这将干扰后续的剖面解释。而经三维曲波阈值迭代法去噪后(图7f),信噪比得到很大的提高(SNR=8.3245dB;PSNR=36.1375dB),有效信号的损失还是最小(MSE=0.1590×10-4)。 图8a和图8b分别为采用二维曲波阈值迭代法和三维曲波阈值迭代法去噪前、后的差值剖面。可以明显看出,经二维曲波阈值迭代法去噪后的差值剖面上存有较明显的同相轴残余,而经三维曲波阈值迭代法去噪后的差值剖面上看不出明显的有效信息。可见即使在低信噪比的情况下,三维曲波阈值迭代法的去噪效果仍然要好于其它3种方法,更符合高信噪比、高保真度的地震资料去噪处理要求。 通过以上模拟数据测试结果的对比分析可以看出,相比于传统的去噪算法,无论原始数据的信噪比高低与否,三维曲波阈值迭代法都能获得令人满意的去噪效果。 选取某海区的实际含噪地震资料进行三维曲波阈值迭代法去噪处理试验。该实际地震资料共236炮,每炮有236道记录,采样点数为1250个。图9a为其中的第130炮原始记录,由图9a可见,声的痕迹,而三维曲波阈值迭代法处理结果由于随机噪声的存在,原始地震记录信噪比较低,2.0s以下同相轴较难分辨,而且记录中还存在大量涌浪噪声。图9b到图9e分别为经中值滤波法、F-X反褶积法、二维曲波阈值迭代法和三维曲波阈值迭代法去噪处理后的结果。图10a和图10b分别为该实际炮记录用二维曲波阈值迭代法和三维曲波阈值迭代法去噪前、后的差值剖面。 图8 低信噪比模拟数据二维曲波阈值迭代法(a)和三维曲波阈值迭代法(b)去噪前、后的差值剖面 在采用中值滤波法去噪后的剖面上(图9b)几乎很难分辨出同相轴,其处理结果基本上不能用于实际生产。F-X反褶积法处理结果(图9c)比中值滤波算法的去噪效果要好一些,但是中部弱反射信息被严重剥蚀。对比二维曲波阈值迭代法(图9d)和三维曲波阈值迭代法(图9e)去噪处理结果可以看出:①在0.5~1.0s的白色箭头所指处,即同相轴的边缘部分,经二维曲波阈值迭代法处理后出现了假频,产生了较大的模糊,从图10的差值剖面上也可以看出这一点;②对比最底部的两处蓝色箭头所指处可见,经二维曲波阈值迭代法去噪后的剖面中有明显的大倾角曲波分量存在;③原始记录在160道附近有一个竖直的涌浪噪声(图中红色箭头所示),在图9d中仍然可以看出涌浪噪声的痕迹,而三维曲波阈值迭代法处理结果(图9e)在去除随机噪声的同时也一并去除了涌浪噪声,同相轴清晰连续;④原始记录中与横坐标成锐角方向有一规则弱反射信息(图中黄色箭头所示),这在原始含噪声剖面中很难分辨,而在图9e中这一规则干扰被清晰地反映了出来,这也体现了三维曲波阈值迭代去噪算法优于其它3种算法,这一点对于实际生产中提取弱反射信息至关重要。 图9 某海区实际地震资料原始炮记录(a)及其中值滤波法(b),F-X反褶积法(c),二维曲波阈值迭代法(d)和三维曲波阈值迭代法(e)去噪处理结果 综上所述,对于多炮地震数据的随机噪声压制,三维曲波阈值迭代算法是一种有效的去噪方法,去噪效果明显优于其它传统算法。 图10 实际地震炮记录二维曲波阈值迭代法(a)和三维曲波阈值迭代法(b)去噪前、后的差值剖面 三维曲波变换是一种多尺度分析方法,它增加的尺度、角度和位置分量给三维曲波变换带来了其它变换不可及的稀疏性,使阈值迭代法的求解精度更高。经模拟数据和实际地震资料去噪处理结果的对比分析可以看出,三维曲波阈值迭代法较常规去噪方法不仅去噪效果突出,而且去噪后有用信息损失较少,是一种有效的多炮地震数据随机噪声去除方法。 同时也应该指出,由于三维曲波变换会产生较高的冗余度,计算三维数据所需的计算时间和存储空间都是巨大的,这一问题限制了其在实际生产中的应用。如何进一步简化其结构,管理数据,减少冗余度,还有待进一步研究。此外,我们采用了三维曲波变换与软阈值迭代法结合的算法,虽然去噪效果比较满意,但是由于软阈值算法的先天缺陷可能会造成信号边缘模糊,不利于具有尖锐边缘的地震资料的处理,因此还需要寻找一种更好的阈值选取方法。 参 考 文 献 [1] 张军华,吕宁,田连玉,等.地震资料去噪方法综合评述[J].石油地球物理勘探,2005,40(增刊):121-127 Zhang J H,Lv N,Tian L Y,et al.Comprehensive review of seismic data denoising[J].Oil Geophysical Prospecting,2005,40(S1):121-127 [2] 康冶,于承业,贾卧,等.f-x域去噪方法研究[J].石油地球物理勘探,2003,38(2):136-138 Kang Y,Yu C Y,Jia W,et al.f-x domain denoising research[J].Oil Geophysical Prospecting,2003,38(2):136-138 [3] 王勇,郦军,张奎凤.基于小波变换的地震信号降噪处理[J].石油物探,1998,37(3):72-76 Wang Y,Li J,Zhang K F.The noise elimination processing of seismic signal based on wavelet transform[J].Geophysical Prospecting for Petroleum,1998,37(3):72-76 [4] Candès E,Donoho D.Curvelets:a surprisingly effective nonadaptive representation of objects with edges[M].Tennessee Nashville:Vanderbilt University Press,1999:1-10 [5] Candès E J,Donoho D L.New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities[J].Communications on Pure and Applied Mathematics,2004,57(2):219-266 [6] Candès E,Guo F.New multiscale transforms,minimum total variation synthesis:applications to edge-preserving image reconstruction[J].Signal Processing,2002,82:1519-1543 [7] Herrmann F J,Verschuur E.Curvelet-domain multiple elimination with sparseness constraints[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,1333-1336 [8] Huub D,Maarten V.Wave-character preserving pre-stack map migration using curvelets[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,961-964 [9] Ying L,Demanet L,Candès E.3-D discrete curvelet transform[J].International Society for Optics and Photonics,2005,5914(13):344-354 [10] Candès E,Demanet L,Donoho D,et al.Fast discrete curvelet transforms[J].SI-AM Multi-scale Modeling and Simulation,2006,5(3):861-899 [11] Herrmann F J,Wang D L,Hennenfent G.Multiple prediction from incomplete data with the focoused curvelet transform[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007,2505-2509 [12] Ramesh N,Domimique G,Mohamed T,et al.Coherent and random noise attenu-ation using the curvelet transform[J].The Leading Edge,2008,27(2):240-248 [13] 张素芳,徐义贤,雷栋.基于Curvelet变换的多次波去除技术[J].石油地球物理勘探,2006,41(3):262-265 Zhang S F,Xu Y X,Lei D.Multiple-eliminated technique based on Curvelet transform[J].Oil Geophysical Prospecting,2006,41(3):262-265 [14] 彭才,常智,朱仕军.基于曲波变换的地震数据去噪方法[J].石油物探,2008,47(5):461-464 Peng C,Chang Z,Zhu S Y.Noise elimination method based on curvelet transform[J].Geophysical Prospecting for Petroleum,2008,47(5):461-464 [15] Wang D L,Rayan S,Yilmazö,et al,Bayesian wavefield separation by transform-domain sparsity promotion[J].Geophysics,2008,73(5):A33-A38 [16] 张恒磊,刘天佑.Curvelet变换及其在地震波场分离中的应用[J].煤田地质与勘探,2010,38(1):76-80 Zhang H L,Liu T Y.Curvelet transform and its application in seismic wave field separation[J].Coal Geology & Exploration,2010,38(1):76-80 [17] 孟大江,王德利,冯飞,等.基于Curvelet变换的稀疏反褶积[J].石油学报,2013,34(1):107-114 Meng D J,Wang D Li,Feng F,et al.Spare deconvolution based on the Curvelet transform[J].Acta Petrolei Sinica,2013,34(1):107-114 [18] Wang D,Sun J,Meng D,et al.Absorption compensation based on curvelet transform[J].Journal of Seismic Exploration,2013,22(1):19-23 [19] Feng F,Wang D L,Zhu H,et al.Estimating primaries by sparse inversion of the 3D Curvelet transform and the L1-norm constraint[J].Applied Geophysics,2013,10(2):201-209 [20] Daubechies I,Defrise M,de Mol C.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J].Communications on Pure and Applied Mathematics,2004,57(11):1413-1457 [21] Elad M,Starck J L,Querre P,et al.Simultaneous cartoon and texture image inpainting using morphological component analysis(MCA)[J].Applied and Computational Harmonic Analysis,2005,19(3):340-358
2 三维曲波阈值迭代法
2.1 三维曲波阈值迭代法实现基础

2.2 三维曲波阈值迭代法实现步骤


3 计算实例
3.1 模拟数据测试算例





3.2 实际地震资料处理试验



5 结束语

