基于t分布为先验约束的叠前AVO反演
印兴耀,周琪超,宗兆云,刘汉卿
(中国石油大学(华东)地球科学与技术学院,山东青岛266580)
叠前AVO反演通过研究地震波振幅随入射角的变化规律,可以从含有丰富动力学信息的叠前地震资料中获得多种反映地下储层物性信息的弹性参数,为储层预测与烃类检测提供定量化的依据[1]。然而,叠前反演是一个严重的病态问题[2],并且易受噪声等不确定性因素的影响。为了获得稳定可靠的反演解,必须对反演过程进行合理的约束。
基于贝叶斯理论框架的叠前三参数反演研究是目前对反演效果进行改善的主流方向,该方法将似然函数与先验地质信息结合,通过求解最大后验概率来建立反演的目标函数,进而反演弹性参数。其中,先验信息的正则约束作用可以较好地解决三参数同时反演所存在的“病态”问题[3],似然函数的构建则可以体现反演目标与地震子波及地震数据的关系。但对于先验信息及似然函数的选择,并没有统一的假设及论述,对此许多学者进行了大量的研究。
Mallick等[4]将贝叶斯统计学的框架引入AVO数据的反演,并用遗传算法实现了AVO数据的波形反演;Buland等[5]通过概率统计分析认为弹性参数特别是纵波速度基本符合高斯分布,并以此构建出贝叶斯反演方法,得到较好地反演结果;Downton[6]在动校正的基础上做了AVO稀疏脉冲波形的反演,得到了反射系数剖面,发现柯西先验比高斯先验分布分辨率更高;Hampson等[7]结合叠后波阻抗公式推导的思想,给出了叠前AVO三参数反演公式;陈建江等[8-9]基于贝叶斯理论,建立了测井数据的参数协方差矩阵约束反演,提高了反演问题的稳定性;杨培杰等[10]验证了改进柯西分布的改良效果,提出了一种基于非线性二次规划的叠前三参数反演方法,能够较好地反演信噪比较低的数据;张世鑫等[11]提出了以三分量柯西分布作为先验函数分布,在利用柯西分布保护弱反射信息的同时考虑了三参数统计的相关特性,得到了较为准确的反演参数;王磊等[12]提出了在先验信息不确定条件下贝叶斯结构的学习方法,提高了贝叶斯框架的可信度;刘洋等[13]提出了针对非高斯噪声的地震叠前反演算法,构造了能同时压制高斯和非高斯噪声的混合范数作为反演的目标函数,较为有效地压制了叠前地震资料中的噪声。
我们在前人研究的基础上,基于贝叶斯理论,以t分布作为先验函数构建叠前AVO反演方法,实现了三参数的约束反演,为储层预测提供了更为可靠的反演参数。
1 t分布
为了提高对先验函数选择的准确性,增加后验函数的可信度,通过对多个地区若干口井的测井数据进行统计分析,发现在绝大部分地区待反演的地层参数更符合t分布,而与高斯、柯西分布存在较大差别,因此,选择t分布作为先验函数更为合理(图1)。
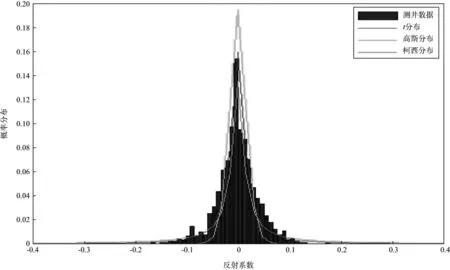
图1 井中待反演参数分布
t分布的概率密度函数是常规的t分布自由度(k)选择值通常为k>1,但在此构建计算过程中,为了在特殊情况下提高分辨率,我们也可以选择k<1。当t分布自由度取1时,t分布成为柯西分布;当自由度取+∞时,t分布成为高斯分布。
(1)
图2给出了不同自由度的t分布与高斯分布及柯西分布的函数曲线对比。由图2可以看出,在构建的贝叶斯理论框架下,先验函数选择高斯分布和柯西分布只是t分布的两个特例,与高斯分布、柯西分布相比,t分布有更大的适用性。

图2 不同自由度的t分布与高斯分布及柯西分布的函数曲线
2 方法原理
2.1 反演流程
我们采用基于t分布作为先验函数构建的贝叶斯叠前AVO反演方法,通过处理过的地震数据和地震子波,直接反演得到弹性参数,具体流程如图3所示。

图3 基于贝叶斯框架的AVO反演流程
2.2 基于t分布为先验函数的贝叶斯方程的建立
由贝叶斯公式得到参数m的后验概率分布为
(2)
式中:m为要估计的参数;x为观测样本;p(m|x)为后验概率;p(m)为先验概率;p(x|m)为似然函数。贝叶斯估计在地震反演中的用法就是由带噪声的观测数据d估计模型参数m。假设地震资料的背景噪声服从高斯分布,则似然函数为
(3)

(4)
式中:σm为模型参数的标准差。由贝叶斯公式[3,14]可得后验概率分布为
(5)
其中,
对后验概率分布取极值(对目标函数取对数,省略常数项,再求导)得

(8)
2.3 模型约束
在有井资料或其他地质资料时,通常用一些简单的数学变换关系式来对目标函数进行趋势约束,使反演结果更精确。
本文中的模型约束矩阵形式写为
(9)
式中:ξ为模型参数对应的井资料数据;P为积分算子矩阵。
将模型约束加入到目标函数,则最终目标函数变为
(10)

(11)
2.4 自由度的选择
由(11)式可以看出,在反演目标函数中,除了噪声和模型的分布方差外,自由度k是反演过程中正则化约束大小的决定性因素。t分布自由度的选择,是决定反演效果的重要因素。对一般地区的处理,可根据反演地区的井数据,通过参数提取进行曲线拟合,以此确定自由度的数值。对于无井地区的自由度选择,可先抽取一个地震道集,通过反演试算确定自由度。
3 模型试算
给定一个雷克子波和反射界面模型,进行无噪与有噪的正演合成,结果如图4所示。
下面验证t分布与柯西分布、高斯分布作为先验函数的反演效果。
1) 当信噪比为4时,合成数据(图5a)质量较好,分别采用柯西分布、t分布以及高斯分布的算法进行反演,得到图5b,图5c和图5d。可以看出,三者均能识别反射层位,柯西分布和t分布的反演结果分辨率相对较高,故应选择柯西分布或自由度相对较小的t分布。
2) 当信噪比为2时,合成数据(图6a)质量一般,分别采用柯西分布、t分布以及高斯分布构建的算法进行反演,得到图6b,图6c和图6d。可以看出,高斯分布的反演结果可以大体分辨反射层位,但波动性较大,精度较低;柯西分布的反演结果精度提高,却产生了“假反射”,误导反射层位的判断;而t分布的反演结果可以较好地反应反射层位,且分辨精度较高。
通过图5和图6可以看出,相对于t分布作为先验函数构建的算法,高斯分布(相当于自由度为+∞的t分布)和柯西分布(相当于自由度为1的t

图4 给定的子波(a)与反射系数(b)正演合成的无噪(c)和有噪(d)数据

图5 信噪比为4时合成数据(a)的柯西分布(b)、t分布(c)及高斯分布(d)反演结果
分布)作为先验函数构建的算法反演效果相对较差。通过图5b和图5c(或者图6b和图6c)的对比,可以发现自由度适当增大可以提高反演的稳定性;通过图5c和图5d(或者图6c和图6d)的对比,可以发现自由度适当减少可以提高分辨率。
为了进一步验证t分布作为先验分布的贝叶斯反演方法的可行性,我们对图7所示的Marmousi模型数据(包括纵、横波速度及密度数据)进行试算。
图8是根据图7中的数据进行不同角度道集叠加的剖面。图9是对图8中的叠加剖面进行基于t分布的叠前AVO反演得到的弹性参数剖面。通过反演出的纵、横波速度和密度剖面(图9)与原始二维地层模型数据(图7)的对比可以看出,二者吻合度较高,且分层较为清晰,细节反演准确,证明了t分布构建的贝叶斯框架反演效果较好,有较高的分辨率和适用性。

图6 信噪比为2时合成数据(a)的柯西分布(b)、t分布(c)及高斯分布(d)反演结果

图7 二维Marmousi地层模型数据a 纵波速度; b 横波速度; c 密度

图8 Marmousi模型数据不同角度道集叠加剖面a 小角度(5°~15°); b 中角度(15°~25°); c 大角度(25°~35°)

图9 Marmousi模型数据基于t分布的叠前AVO反演得到的弹性参数a 纵波速度; b 横波速度; c 密度
4 实际资料处理
为了验证本文方法处理实际资料的有效性和实用性,对某地区实际地震资料的叠前角道集进行弹性参数反演。分别采用基于柯西分布、t分布和高斯分布作为先验函数构建的算法进行反演,对反演得到的结果与测井数据进行对比分析。
图10是该地区纵波速度的反演结果,可以看出,基于3种分布的算法均能较好地反演出纵波速度,但在一些细节部位(见图中蓝圈标示),t分布还是具有较好的改善功能。
图11是该地区横波速度的反演结果,可以看出,t分布作为先验函数构建的反演算法(图11b)比柯西分布、高斯分布作为先验函数构建的反演算法(图11a,图11c)反演效果明显改善(见图中蓝圈标示),反演的数据更切合真实值。
图12是该地区密度信息的反演结果,可以看出,密度反演相对于纵、横波速度反演精确度明显下降,但以t分布为先验函数的反演算法(图12b)比柯西分布、高斯分布作为先验函数的反演算法(图12a,图12c)整体效果要好,反演出的密度基本可以较好地刻画地层岩石的真实密度。

图10 实际资料反演得到的纵波速度(黑色曲线)与测井纵波速度(红色曲线)对比a 柯西分布; b t分布; c 高斯分布

图11 实际资料反演得到的横波速度(黑色曲线)与测井横波速度(红色曲线)对比a 柯西分布; b t分布; c 高斯分布

图12 实际资料反演得到的密度(黑色曲线)与测井密度(红色曲线)对比a 柯西分布; b t分布; c 高斯分布
通过图10至图12的对比分析表明,针对实际地震资料,t分布构建的贝叶斯框架反演方法反演精度更高,适用性更好,可以得到更为可靠的弹性参数反演结果,从而更为准确地预测储层流体。
5 结束语
1) 模型数据和实际资料的叠前反演结果表明,t分布作为先验概率分布更符合实际地层参数分布,反演效果更好。
2) 对于t分布的自由度选取,应对测井数据进行曲线拟合,得到初始自由度。
3) 对t分布自由度的选择还应考虑实际地震资料的采集、处理情况,若反演初始资料质量相对较高,则应选择较小的自由度;若反演初始资料质量相对较低,则应选择较大的自由度。
参 考 文 献
[1] Downton J E.Seismic parameter estimation from AVO inversion[M].Calgary:University of Calgary,2005:1-371
[2] Tarantola A.Inverse problem theory and methods for model parameter estimation[M].Philadelphia:Society of Industrial and Applied Mathematics,2005:1-342
[3] Ulrych T J,Sacchi M D,Woodbury A.A Bayes tour of inversion:a tutorial[J].Geophysics,2001,66(1):55-69
[4] Mallick S.Model-based inversion of amplitude variations with offset data using a genetic alporithm[J].Geophysics,1995,60(4):939-954
[5] Buland A,Omre H.Bayesian linearized AVO inversion[J].Geophysics,2003,68(1):185-198
[6] Downton J E,Lines L.Constrained three parameter AVO inversion and uncertainty analysis[J].Expanded Abstracts of 71stAnnual Internet SEG Mtg,2001,251-254
[7] Hampson D P,Russell B H,Bankhead B P,et al.Simultaneous inversion of pre-stack seismic data[J].Expanded Abstracts of 75thAnnual Internet SEG Mtg,2005,1633-1637
[8] 陈建江,印兴耀.基于贝叶斯理论的AVO三参数波形反演[J].地球物理学报,2007,50(4):1251-1260
Chen J J,Yin X Y.Three-parameter AVO waveform inversion based on Bayesian theorem[J].Chinese Journal of Geophysics,2007,50 (4):1251-1260
[9] 陈建江.AVO 三参数反演方法研究[D].山东青岛:中国石油大学,2007
Chen J J.Study of three-term AVO Inversion Method[D].Qingdao:China University of Petroleum,2007
[10] 杨培杰,印兴耀.非线性二次规划贝叶斯叠前反演[J].地球物理学报,2008,51(6):1876-1882
Yang P J,Yin X Y.Non-linear quadratic programming Bayesian prestack inversion [J].Chinese Journal of Geophysics,2008,51(6):1876-1882
[11] 张世鑫,印兴耀,张繁昌.基于三变量柯西分布先验约束的叠前三参数反演方法[J].石油地球物理勘探,2011,46(5):737-747
Zhang S X,Yin X Y,Zhang F C.Prestack three term
inversion method based on Trivariate Cauchy distribution prior constraint[J].Oil Geophysical Prospecting,2011,46(5):767-747
[12] 王磊,刘明辉,王维平.先验信息不确定条件下贝叶斯网结构学习方法[J].计算机工程与应用,2010,46(16):39-41
Wang L,Liu M H,Wang W P.Structure learning method of Bayesian network with uncertain prior information [J].Computer Engineering and Applications,2010,46(16):39-41
[13] 刘洋,张家树,胡光岷,等.叠前三参数非高斯反演方法研究[J].地球物理学报,2012,55(1):269-276
Liu Y,Zhang J S,Hu G M,et al.Study of three-term non-Gaussian pre-stack inversion method[J].Chinese Journal of Geophysics,2012,55(1):269-276
[14] Lindley V.Introduction to probability and statistics from a Bayesian viewpoint[M].London:Cambridge University Press,1965:1-292

