碳酸盐岩储层孔隙度预测方法研究及其在南海某区的应用

刘开元，贺振华，许艳秋

(1.成都理工大学油气藏地质及开发工程国家重点实验室，四川成都610059;2.成都理工大学地球物理学院，四川成都610059)

在油气勘探开发过程中，孔隙度是描述储层储集能力的一个非常重要的参数。通常情况下，孔隙度的预测都是通过与其它弹性参数的映射关系计算得来。而目前难以直接从地震资料中计算孔隙度，因为孔隙度与地震数据中的弹性参数之间没有直接的对应关系，并且传统预测孔隙度的方法对于横向变化较大的碳酸盐岩储层没有良好的适应性。由此我们提出了一种新的孔隙度预测方法，以适应碳酸盐岩储层孔隙度预测的需要。

孔隙度预测方法主要分为线性计算方法和非线性反演方法两大类。线性计算方法包括：①直接使用Wyllie等[1]的时间平均方程进行计算，但该方法不适用于复杂的地质条件，Raymer等[2]对其进行了修正，诸多学者也提出了一些适用于不同模型的孔隙度计算公式[3-5];②传统方法，利用测井曲线的各弹性参数与孔隙度建立线性或非线性关系得到孔隙度与各弹性参数的统计关系式，再利用地震弹性反演所得到的弹性参数映射计算得到孔隙度;③张应波[6]提出了基于Biot-Gassmann理论无井资料约束并能预测二维地震数据孔隙度的方法，由于计算过程中需要输入的参数过多，且参数获取较为困难(如应力、孔隙流体压力、流体粘滞系数、孔隙能量及其它子参数)，该方法未能得到广泛应用。非线性反演方法主要包括神经网络(ANN)方法[7]、数据组合处理方法(GMDH)[8]和随机模拟法等，这类方法没有考虑孔隙类型对地震波的影响，反演的孔隙度没有可靠的理论基础，非线性孔隙度预测的应用受限。

Nur等[9]、Avseth等[10]和Vernik等[11]指出相同的孔隙度造成声波差异大的主要原因是孔隙结构不同。受沉积环境变化及成岩作用多样性的影响，会形成极其复杂的孔隙类型。孔隙的大小、形状、空间展布、孔喉半径的粗细及其连通关系都会影响声波的传播路径及传播时间。诸多学者通过岩石物理测试等手段发现孔隙结构对于碳酸盐岩的岩石弹性性质的影响很大，如：Zimmerman[12]和Kachanov[13]通过研究二维及三维孔隙形状指出，孔隙形状是影响岩石弹性性质的重要因素;Eberli等[14]发现在碳酸盐岩中声波速度与孔隙度及孔隙类型都有关;Sun[15]发现孔隙度相同但孔隙类型不同的碳酸盐岩声波速度存在较大的差异，渗透率的差异也很大;Weger等[16]利用数字图像分析仪测试碳酸盐岩中孔隙的几何空间分布，发现孔隙结构与地质属性及声学特征存在一定的联系，并建立了它们之间的关系。这些研究充分说明，在碳酸盐岩中，孔隙类型和孔隙结构是影响岩石弹性性质和声波速度的重要因素，而含孔隙岩石的弹性性质与孔隙度密切相关，因此，预测孔隙度时考虑孔隙结构因素是必要的。

我们利用测井数据(纵、横波速度，密度，孔隙度，含水饱和度)计算出单井参数(岩石饱和流体等效压缩系数、岩石基质压缩系数)，根据考虑了孔隙结构模型的孔隙度计算公式，利用地震弹性反演的三参数数据，计算得到某地区的孔隙度。通过工区碳酸盐岩储层孔隙度预测试验，得到的孔隙度与测井孔隙度吻合很好，并能很好地适用于碳酸盐岩储层孔隙度的预测。

1 理论基础

1.1 碳酸盐岩孔隙类型及孔隙结构

碳酸盐岩中的孔隙可以根据其大小、可识别性、成岩作用及几何复杂程度来进行分类，这些分类在识别油气物理属性上很有用处，而且这些孔隙描述对于地球物理响应特征而言更具挑战性。这是因为地震波波长通常比微观结构的尺寸大很多，因此地震波只能体现众多复杂孔隙结构所造成的平均影响，而不能体现单个孔隙或裂缝所造成的影响。由此，将碳酸盐岩中复杂的孔隙网络简化为3种孔隙类型来合理反映它们对于声波和压力的响应。这3种孔隙类型[17]为：①参考孔隙，作为背景趋势在晶粒间大量连续的存在，为碳酸盐岩中最主要的孔隙类型(图1a);②高扁率孔隙，代表印模孔隙或溶蚀孔隙，常常是由溶解的颗粒及化石腔室所形成(图1b);③具有小扁率的裂纹孔隙，代表微裂缝结构(图1c)。它们的形成都可能发生在碳酸盐岩成岩作用期间，包括压实作用、断层错动作用、溶解崩塌作用等。

图1 显微镜下不同孔隙的岩石薄片a 参考孔隙; b 高扁率孔隙; c 小扁率的裂纹孔隙

孔隙结构表征合理才能更好地在孔隙度预测中体现出孔隙结构对于孔隙度的影响，从而使得孔隙度的计算更为合理，并能更好地反映碳酸盐岩储层中孔隙的类型，为识别有效储层奠定充分可靠的基础。通常情况下，孔隙结构是指岩石中孔隙的大小、形状、相互连通关系及受储层界面现象有关的表面张力、吸附作用、湿润度、毛细管作用等的影响，国内外研究学者常将孔隙结构与固结度、孔隙扁率、压力、压缩系数等岩石弹性参数相联系。但是孔隙结构参数的具体形式至今尚未确定，由此He等[18]提出了统一的岩石骨架模型与公式：

(1)

式中：βD和βS分别为岩石骨架压缩系数和岩石基质压缩系数;μD和μS分别为岩石骨架剪切模量和岩石基质剪切模量;η为岩石孔隙度;p,q和q*是岩石结构参数，为可调节参数。分别对p，q进行特殊赋值，得到不同的岩石孔隙物理模型，此岩石骨架模型将孔隙结构相关的参数(如：固结度、临界孔隙度、孔隙扁率等)进行了有机的结合，便于合理选择岩石骨架模型进行孔隙度计算。

1.2 孔隙度预测综合计算公式

以岩石压缩系数为参数的Gasssmann方程[19]一般表示为

(2)

式中：βE为岩石饱和流体等效压缩系数;βP为岩石孔隙流体压缩系数;μE为岩石饱和流体等效剪切模量;其它参数的意义如(1)式。

在双相介质中，储层的岩石孔隙流体压缩系数βP远大于岩石基质压缩系数βS。碳酸盐岩基质矿物刚度大，压缩系数更小，因此对于碳酸盐岩储层而言，上述情况更为明显。表1定量给出了碳酸盐岩矿物基质压缩系数与其它压缩系数的对比结果[20]。可用βP来近似代替βP-βS，并且储层埋藏越深，年代越久，成岩作用越大，两者相差越大。由此可见，对于碳酸盐岩采用上述近似来建立新的Gassmann方程是可行的[21]。由(2)式可得

表1 不同压缩系数对比

将岩石骨架模型的综合表达式(1)式代入(3)式得到基于Gassmann方程的计算孔隙度的综合表达式：

(4)

对于饱和流体岩石，在不排水情况下，βE≈βS，βE-βS≪βP，令

(5)

将(4)式简化为

(6)

(6)式即为孔隙度的计算公式。其中，C为岩石孔隙结构参数，与孔隙形状、固结度、胶结程度等相关。

公式(5)中，选取不同的p和q可得到不同岩石骨架模型所对应的孔隙结构参数C，并通过(6)式得到孔隙度，其中,βS通过文献[22]中的自适应基质压缩系数反演方法来求取,而

(7)

式中:vP,vS,ρ分别为岩石的纵、横波速度及密度。

2 实际资料应用

以南海某区为例，研究目的层为新近系碳酸盐岩储层。测井资料分析结果显示，孔隙度为5%～12%的储层含油气的可能性较大，而孔隙度大于20%的储层含水的可能性较大。利用孔隙度预测结果来划分有利区带，然后通过流体识别方法对有利区带进行油气预测，这样对缩小寻找目标，提高钻遇率可起到重要作用。

2.1 测井数据试算

我们选择研究区中处于一个相带内且相对较近的两口井(H1，H2)来验证本文孔隙度预测方法的效果。其中，含有横波测井资料的H1井为已知井，对H2井进行孔隙度预测。首先根据测井数据计算H1井的βE和βS(图2)，通过βE/βS与其它弹性参数的交会分析得到与βE/βS相关性最好的弹性参数(图3)，可以看到，vP与βE/βS的相关系数可以达到0.9893(图3a)；然后直接使用vP与βE/βS的拟合关系式由vP计算出孔隙结构参数C，再通过C与其它弹性参数(如纵波速度、横波速度、纵波模量及纵横波速度比等)的交会分析(图4)，得到与C相关性最好的弹性参数vP(图4a)，并通过此映射关系式来计算H2井的孔隙结构参数C，

代入(6)式得到H2井的孔隙度计算式：

(8)

图5为本文方法与传统方法的孔隙度预测结果对比。从图5中可以看到，本文方法预测孔隙度与实测孔隙度误差小，精度明显高于传统方法预测结果，说明本文方法可行、有效。

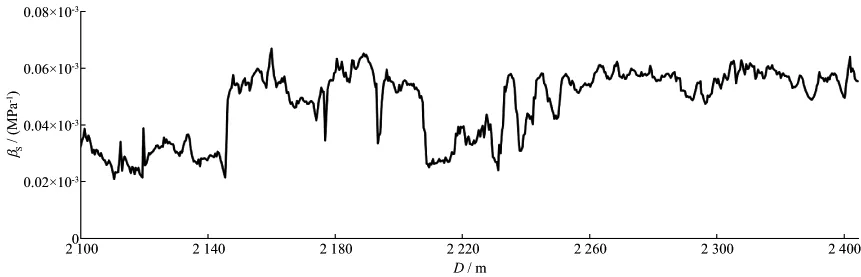
图2 测井数据计算的H1井的βS曲线

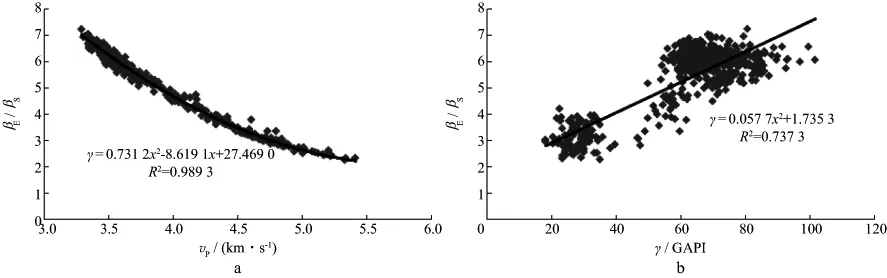
图3 H1井βE/βS与vP(a)和γ(b)的交会分析结果

图4 H1井C与和vP/vS(d)的交会分析结果

2.2 实际地震资料应用

实际地震资料应用与测井数据试算步骤一致，只是孔隙度计算中vP2,vS2和ρ2采用实际工区叠前地震反演的三参数数据，这样便可得到受H1井约束的整个工区孔隙度预测三维数据体。图6为过H1井的孔隙度预测剖面，可以看到预测结果与原始测井解释的孔隙度吻合度很高。图7a与图7b分别为碳酸盐岩储层顶界面向下20ms与碳酸盐岩储层底界面的预测孔隙度切片，可以看到，H1井和H2井所在位置的孔隙度约为27%～30%，两口井处孔隙度较大，含水的可能性较大。从试油报告分析可知，高孔隙地层往往含水，此处不是良好的储层。实际钻井资料印证了该地层含水，证明预测结果可信。从图7a可以看到，油气有利区带应该在深绿色区域，在该区域寻找孔隙度范围在12%左右的区域，并结合有利圈闭及该区域的油气预测结果，最终确定钻探目标。

图5 本文方法与传统方法孔隙度预测结果对比

图6 过H1井孔隙度预测剖面

图7 碳酸盐岩储层顶面向下20ms(a)和底面(b)的孔隙度预测切片

3 结束语

基于岩石综合骨架模型的孔隙度预测方法以点到面的方式更好地适应碳酸盐岩储层横向变化大的特点，从测井数据试算和实际地震资料应用效果的分析得到4点认识。

1) 岩石孔隙结构和孔隙度同为描述岩石孔隙特性的重要参数，在孔隙度预测中同时考虑孔隙结构的影响在理论和实践上是必要、可行的。

2) 我们导出的岩石孔隙结构参数C，综合了孔隙的各种特征，有一定的代表性和实用价值。

3) 测井数据试算和实际地震资料应用的效果表明，我们提出的考虑了孔隙结构影响的孔隙度预测方法是正确、有效的。

4) 地震叠前弹性反演是我们提出孔隙度预测方法的基础，提高弹性反演的可靠性和精度对孔隙度预测效果有重要作用。

参 考 文 献

[1] Wyllie M R J,Gregory A R,Gardner L W,et al.Elastic wave velocities in heterogeneous and porous media [J].Geophysics,1956,21(1):41-70

[2] Raymer L L,Hunt E R,Gardner J S.An improved sonic transit time-to-porosity transforms [J].Society of Petrophysicists and Well-Log Analysts,1980,21:1-13

[3] Hamilton E L,Bachman R T,Berger W H,et al.Acoustic and related properties of calcareous deep-sea sediments [J].Journal of Sedimentary Petrology,1982,52(3):733-753

[4] Han D A,Nur A,Morgan D.Effect of porosity and clay content on wave velocities in sandstones [J].Geophysics,1986,51(11):2093-2107

[5] Kahraman S,Yeken T.Determination of physical properties of carbonate rocks from P-wave velocity [J].Bulletin of Engineering Geology and the Environment,2008,67(2):277-281

[6] 张应波.地震孔隙率反演方法和应用[J].石油地球物理勘探,1994,29(3):261-273

Zhang Y B.A new method for seismic porosity inversion and its application[J].Oil Geophysical Prospecting,1994,29(3):261-273

[7] Emilson P L,ALexandre C V.3D porosity prediction from seismic inversion and neural networks [J].Computers & Geosciences,2011,37(8):1174-1180

[8] Nahser M A,Wang Y H.Porosity prediction using the group method of data handling [J].Geophysics,2011,76(5):O15-O22

[9] Nur A，Marion D,Yin H.Wave velocities in sediments[C]∥ Hovem J M,Richardson M D,Stoll R D.Shear waves in marine sediments.Dordrecht,Netherlands:Kluwer Academic Publishers,1991:131-140

[10] Avseth P,Wijngaarden A-J V,Flesche H,et al.Seismic fluid prediction in poorly consolidated and clay laminated sands[J].Expanded Abstracts of 67thEAGE Annual Conference,2005,Z99

[11] Vernik L,Kachanov M.Modeling elastic properties of siliciclastic rocks [J].Geophysics,2010,75(6):E171-E182

[12] Zimmerman R W.Compressibility of two-dimensional cavities of various shapes [J].Journal of Applied Mechanics,1986,53(3):500-504

[13] Kachanov M.Effective elastic properties of cracked solids:critial revies of some basic concepts[J].Applied Mechanics Reviews,1992,45(8):304-335

[14] Eberli G P,Batzle M L,Anselmetti F S,et al.Factors controlling elastic properties in carbonate sediments and rocks [J].The Leading Edge,2003,22(7):654-660

[15] Sun Y F.A two-parameter model of elastic wave velocities in rocks and numerical avo modeling [J].Journal of Computational Acoustics,2004,12(4):619-630

[16] Weger R J,Baechle G T,Eberli G P,et al.Quantification of pore structure and its effect on sonic velocity and permeability in carbonates [J].AAPG Bulletin,2009,93(10):1297-1317

[17] Zhao L X,Nasser M,Han D H.Quantitative geophysical pore-type characterization and its geological implication in carbonate reservoirs [J].Geophysical Prosecting,2013,61(4):827-841

[18] He X L,He Z H,Wang X B,et al.Rock skeleton models an seismic porosity inversion [J].Applied Geophysics,2012,9(3):349-258

[19] Gassmann F.Uber die elastizitat poroser medien[J].Gesellschaft in Zurich,1951,96(3):1-23

[20] Mavko G,Mukerji T,Dvorkin J.The rock physics handbook:tools for seismic analysis in porous media [M].Cambridge:Cambridge University Press,1998:91-100

[21] He X L,He Z H,et al.Calculations of rock matrix modulus based on a linear regression relation [J].Applied Geophysics,2011,8(3):155-162

[22] Lin K,Xiong X J,He Z H,et al.Self-adapting extraction of matrix mineral bulk modulus and verification of fluid substitution [J].Applied Geophysics,2011,8(2):110-116