起伏地表下基于抛物插值的最短路径射线追踪
桑运云,孙军晓,焦淑萍,金艳萍,陈院生
(1.中国石油天然气集团公司东方地球物理勘探有限责任公司研究院华北分院,河北任丘062552;2.中国石油天然气集团公司东方地球物理勘探有限责任公司研究院处理中心,河北涿州072751)
随着地震勘探技术的发展和勘探规模的扩大,起伏地表条件下的地震勘探越来越普遍[1-2],通过有效的近地表速度建模方法解决静校正问题成为地震资料处理的重点。初至波层析速度建模由于对初始模型的依赖性小,可以直接由初至波旅行时差反演近地表速度,精确地反演速度场的长波长分量,因而是常用的近地表速度建模方法。
初至波层析的关键是初至波旅行时计算和射线路径的追踪,关系到微商矩阵的准确性和走时残差误差的大小,因此需要相对精确的初至波旅行时射线追踪方法。传统的射线追踪方法各有优缺点:试射法通过迭代修改初始入射角获得了准确的射线路径,但计算比较耗时;弯曲法利用最小走时条件描述射线走时方程,然后迭代修改射线得出正确的射线路径,但常常会陷入局部收敛;波前法将地下介质网格化,利用网格节点连线近似射线路径,但是射线路径常常为折线。起伏地表条件下射线追踪的关键技术是起伏地表的网格化。岳玉波等[3]研究的初值射线追踪方法首先根据三次样条函数及线性函数来描述起伏地表以及地下界面,然后给定射线的初始点和初始方向,逐步计算射线路径,因此计算精度在很大程度上依赖于逐步迭代追踪的步长。Cassell[4]采用网格剖分方法将地下介质划分为很多小块,每块速度为常数,按照一定初始条件从震源处逐个网格进行射线追踪,得到的射线路径在每个网格内都为直线段。Langan等[5]在此基础上将网格内的速度用梯度表示,用曲线表示射线路径,提高了效率和精度。但是以上方法都不能精确地实现炮点和检波点的点对点射线路径追踪,只能近似表示两者之间的射线路径。Moser[6]提出的最短路径射线追踪方法采用节点树的形式实现了初至波射线追踪,但得到的射线路径往往成“之”字形。张建中等[7]利用线性插值方法改进了最短路径射线追踪方法,克服了射线路径只能走网格节点的缺陷,实现了动态网格射线追踪,但是在近地表条件下走时变化往往不满足线性规律。
我们将初至波路径射线追踪方法——基于抛物旅行时插值(PTI)的最短路径射线追踪方法[8]扩展到起伏地表条件下,将起伏地表及地下界面精确地投影到剖分网格节点上,实现了起伏地表条件下的初至波路径的射线追踪。
1 基于PTI的最短路径射线追踪方法原理
基于PTI的最短路径射线追踪方法(以下简称PTISPR法)分两步进行:①正向波前扩展,即从震源开始计算整个速度场的所有节点的最小走时;②反向追踪路径,即从接收点开始向震源反向追踪射线路径。其核心思想是:首先利用Dijkstra[9]算法计算某节点旅行时,然后在计算过程中搜索满足抛物插值的节点并进行插值,将最小旅行时作为该计算节点的最终时间。射线追踪过程是利用抛物旅行时插值从接收点网格开始一直追踪到炮点网格。若A,B,C为同一边界上已知走时的3个节点,其坐标分别为(xA,zA),(xB,zB),(xC,zC),对应的走时为tA,tB,tC,则它们构成了节点D的插值段,求该边界上从R点(xR,zR)到达D点(xD,zD)的最小旅行时tD和射线路径所利用的插值公式是[8]
(1)
其中,LAB=xA-xB,LAC=xA-xC,LBC=xB-xC;s为慢度。
2 起伏地表条件下PTISPR法射线追踪的实现
2.1 待求旅行时的节点数量
PTISPR法射线追踪分向前和向后两个过程,向前计算每个节点的旅行时[6],向后追踪射线路径。将起伏地表网格化,如图1所示,地表上速度为0,地表面以上速度区域为无效区域,不需要计算节点时间。因此,首先需要找出速度场的有效区域以及要计算旅行时的节点数。如图2所示,节点A和节点B为相邻两个横向采样点,求取两者所在的网格范围内A节点所属的无效节点数(即A节点及其以上采样点对应的边界节点和角节点无效节点数目)。
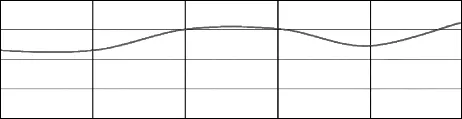
图1 起伏地表图示
1) 节点A和节点B纵向采样值相等(图2a)。图2a中①表示A和B都为角点节点;②表示A为角点节点,B为下边界节点;③表示A为下边界节点,B为角点节点或下边界节点。
2) 节点A的纵向采样值大于节点B的纵向采样值(图2b)。根据A和B的坐标位置,可以得到连接A,B的直线段,然后依次求取与A及A以上节点对应的右边界的交点,若节点的横向位置小于交点横向位置,则为无效节点。对于A节点对应的下边界节点,则根据A的纵向坐标计算。
3) 节点A的纵向采样值小于节点B的纵向采样值(图2c)。计算原理同2),仅仅当节点的横向位置大于交点横向位置时,为无效节点。
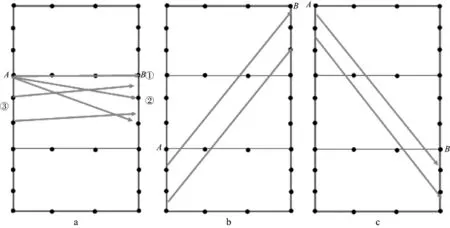
图2 起伏地表在一个网格内的不同分布情况a 节点A,B纵向采样值相等; b 节点A纵向采样值大于节点B; c 节点A纵向采样值小于节点B
2.2 速度场的处理
受网格化和起伏地表的影响,在起伏地表范围内常常会出现角节点为无效节点而边界节点为有效节点的情况,在求取网格或路径速度时就会出现某一节点采样值对应的速度为0的结果,进而影响网格内速度和某一射线路径速度的计算。解决方法是:当某一节点采样值对应的速度为0时,说明此计算节点为边界节点,因此首先判断其属于右边界节点还是下边界节点,若为右边界节点则将采样值横向加1,纵向不变,得到的采样值对应的速度作为该节点的速度;若为下边界节点则将采样值纵向加1,横向不变,得到的采样值对应的速度作为该节点的速度。
2.3 插值
抛物插值是根据某一网格内已知的相邻3个节点时间求其它节点的时间。在起伏地表所处的网格边界,相邻3个节点会出现3种情况:①相邻3个节点时间全部已知;②相邻两个节点时间已知,另一个为无效节点;③有两个节点为无效节点,仅有一个节点时间已知。因此,在起伏地表射线追踪过程中,需要对网格边界上的节点进行判断,对应上述3种情况分别进行抛物插值、线性插值和直接计算两节点的直线时间。
2.4 起伏地表所在网格内射线路径的确定
射线路径的确定是从接收点开始向炮点位置反向追踪的过程,当追踪到炮点所处的网格时,需要判断当前接收点和炮点是否在同一个网格范围内。由于起伏地表的存在,射线路径在同一网格内经过的网格点数往往大于2,使射线路径出现折线形状。处理方法是:当接收点和炮点坐标横向距离不大于横向采样间隔时,若纵向距离不大于纵向采样间隔的1/2,则直接将接收点修正为炮点;同理,当接收点和炮点坐标纵向距离不大于纵向采样间隔时,若横向距离不大于横向采样间隔的1/2,则直接将接收点修正为炮点。
2.5 模型试算
2.5.1 起伏地表水平层状模型
图3是加入了起伏地表的4层水平模型速度场(600m×600m)。将模型网格化,横向和深度采样间隔都为4m,网格数为151×151。炮点位于起伏地表横向300m处,模型底部和两个边界接收,共83道,道间距为20m。其中底部31道,第1道坐标为(0,599m);两个边界各26道,第1个接收点位置坐标分别为(0,80m),(600m,80m)。图4是采用PTISPR法由上述观测系统得到的等时线和射线路径,从等时线图上可以明显看到3个分界面处波前面发生的变化(图4a),从射线路径图上可以看到直达波和折射波两种不同类型的初至波路径(图4b)。
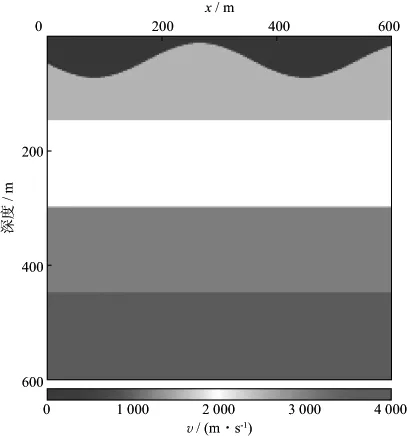
图3 起伏地表水平层状模型

图4 起伏地表水平层状模型等时线(a)和射线路径(b)
2.5.2 起伏地表连续介质模型
图5为起伏地表连续介质速度模型(1500m×500m),速度场从浅到深的变化范围为300~2800m/s,网格节点数为101×101,横向采样间隔15m,深度采样间隔5m。地面地震观测系统:炮点和接收点都位于起伏地表,模型中间位置放炮,两边接收,第1道横向位置0,道间隔30m,共51道。图6显示了应用PTISPR法由上述观测系统得到的回折波射线路径和对应的等时线,可见起伏地表连续介质模型对应的等时线是一系列半径随深度增加的圆弧,射线是从震源出发向下到达某一深度后又向上拐回地面到达观测点的两套圆弧射线,称为“回折波”。

图5 起伏地表连续介质模型

图6 起伏地表连续介质模型等时线(a)和射线路径(b)
3 起伏地表条件下PTISPR法初至波走时层析
对于某一模型速度场,初至波层析速度分析大体流程为:
1) 建立初始速度模型;
2) 分别对初始速度场和模型速度场进行初至波路径射线追踪,由此得到初至波旅行时(将初始速度场和模型速度场的旅行时相减得到的走时残差)和层析所需的微商矩阵(射线在每个网格内的路径长度);
3) 建立层析方程组[10]AΔs=Δt,其中A为微商矩阵,Δt为初始速度场和模型速度场的初至旅行时差,Δs为慢度更新量;
4) 求解层析方程组得到慢度更新量,更新初始模型,然后转至步骤2);
5) 如此迭代,直到更新后的速度场满足需要(两次迭代旅行时变化很小,速度改变量很小)为止。
3.1 模型试算
图7所示为含起伏地下界面起伏地表模型的真实速度场(1500m×1500m),采样点数为101×301,横向采样间隔15m,深度采样间隔5m。地面地震观测系统:炮点和检波点都位于起伏地表,第1炮横向位置0,炮间隔250m,共7炮;每炮
101道接收,初始道横向位置0,道间隔15m。初始速度场深层速度与真实速度场一致,浅层是梯度模型;迭代18次后平均走时残差由-160.0000ms下降到-0.0078ms,得到图8所示的层析建模速度场。与真实速度场(图7)比较可见,近地表低频信息得到了很好的反演,基本上反映了低、降速带内速度变化的趋势。图9为真实速度和层析速度的等时线和射线路径,可见两者基本吻合。经过模型试算,证明起伏地表PTISPR法可以用于近地表建模。
3.2 实际资料试算
某地形起伏地区实际地震资料的炮检排列沿南北走向,每个排列50炮。沿南北向网格间隔100m,深度采样间隔5m,网格化后采样点数为321×121。根据微测井和小折射资料,构建沿深度递增的梯度初始模型,梯度变化量为25m/s。图10a 为初始速度场,图10b为层析建模速度场。由图10可见,通过对初始模型(图10a)进行迭代处理,得到的层析建模速度场(图10b)从南到北高程变化剧烈,呈现南低北高的趋势,北侧低、降速带范围埋深更浅,符合实际地形特征。利用层析建模得到的速度场计算静校正量并对原始炮集进行静校正[11],图11为某单炮记录初至层析静校正前、后的结果。从图11可见,静校正前(图11a)同相轴偏离双曲规律,抖动比较剧烈,初至同相轴不连续;经过静校正后(图11b),抖动现象消除,同相轴更加符合双曲规律,初至同相轴连续性更好。实际资料试算结果证明本文提出的PTISPR法适用于起伏地表情况下地震资料的初至层析静校正处理。

图7 含起伏地下界面的起伏地表模型真实速度场

图8 含起伏地下界面的起伏地表模型层析速度场

图9 含起伏地下界面的起伏地表模型真实速度和层析速度对应的等时线和射线路径a 真实速度等时线; b 层析速度等时线; c 真实速度射线路径; d 层析速度射线路径

图10 起伏地表区实际地震资料层析初始速度场(a)和建模速度场(b)

图11 起伏地表区实际地震资料单炮记录静校正前(a)和初至层析静校正后(b)
4 结束语
射线追踪是走时层析的核心技术。良好的初至波射线追踪方法可以得到精确的初至走时和准确的层析核函数,进而保证层析方程组的准确性,得到更好的层析反演速度场。PTISPR方法在起伏地表条件下可以正确地追踪初至波射线路径,是初至波走时层析速度建模的核心技术。理论模型和实际资料试算结果证明,本文提出的PTISPR法是正确有效的,适用于起伏地表条件下的初至走时层析建模和静校正。
参 考 文 献
[1] 刘玉柱,程玖兵,董良国.面向起伏地表偏移成像的表层静校正方法[J].石油物探,2012,51(6):584-589
Liu Y Z,Cheng J B,Dong L G.A new static correction method for the migration from rugged topography[J].Geophysical Prospecting for Petroleum,2012,51(6):584-589
[2] 宋桂桥,于世焕.山前带地震勘探技术进展与对策研究[J].石油物探,2012,51(6):539-547
Song G Q,Yu S H.Progress and strategy of the seismic exploration in foothill area[J].Geophysical Prospecting for Petroleum,2012,51(6):539-547
[3] 岳玉波,孙建国,杨昊,等.起伏地表下初值射线追踪的实现[J].勘探地球物理进展,2007,30(5):388-391
Yue Y B,Sun J G,Yang H,et al.Realization of initial value ray tracing for rugged topography[J].Progress in Exploration Geophysics,2007,30(5):388-391
[4] Cassel B R.A method for calculating synthetic seismograms in laterally varying media[J].Geophysical Journal International,1982,69(2),339-354
[5] Langan R T,Lerche I,Cutler R T.Tracing of rays through heterogeneous media:an accurate and efficient procedure[J].Geophysics,1985,50(9),1456-
1465
[6] Moser T J.Shortest path calculation of seismic rays[J].Geophysics,1991,56(1):59-67
[7] 张建中,陈世军,许初伟.动态网络最短路径射线追踪[J].地球物理学报,2004,47(5):889-904
Zhang J Z,Chen S J,Xu C W.A method of shortest path raytracing with dynamic networks[J].Chinese J Geophys(in chinese),2004,47(5):889-904
[8] 桑运云,李振春,张凯.基于抛物旅行时插值的最短路径射线追踪[J].石油地球物理勘探,2013,48(3):403-409
Sang Y Y,Li Z C,Zhang K.Shortest path raytracing based on parabolic traveltime interpolation[J].Oil Geophysical Prospecting,2013,48(3):403-409
[9] Dijkstra E W.A note on two problems in connection with graphs [J].Numerische Mathematik,1959,1(1):269-271
[10] Stork C,Clayton R W.Linear aspects of tomographic velocity analysis [J].Geophysics,1991,56(4):483-495
[11] 韩晓丽,杨长春,麻三怀.复杂山区初至波层析反演静校正[J].地球物理学进展,2008,23(2):475-483
Han X L,Yang C C,Ma S H.Static of tomographic inversion by first break in complex areas [J].Progress in Geophysics,2008,23(2):475-483

