致密油藏多段压裂水平井初始产能影响因素分析

杨俊峰,芮捍东,田建波,马春红

(中国石化国际石油勘探开发有限公司,北京 100029)

国内外研究低渗透油藏压裂水平井产能模型通常假设渗流系统为水力压裂缝和油藏两套渗流系统[1-2]。这种假设在研究低渗透油藏中是适用的，但是针对非常规的致密油气藏是不适用的。由于致密油气藏中的基质渗透率非常低，往往是微达西级别的，流体在这种基质系统中流动性非常差。通过矿物岩石学研究发现，致密油藏的储层中，有不同程度的天然裂缝发育，正是这些天然裂缝的发育，才使致密油藏具有开发的潜力。

通过水力压裂创造人工压裂缝，可以有效改变水平井筒附近的地应力分布，同时通过水力压裂缝为桥梁，来增强天然裂缝与水平井筒之间的联系，也可以增加基质系统与天然裂缝、水力压裂缝之间的接触表面积，从而改善基质系统的流动因子，增强基质系统向裂缝系统的供液能力。

1 多段压裂水平井初始产能模型

微裂缝发育的致密油气藏系统中，存在着基质孔隙度和裂缝孔隙度，以及基质渗透率和裂缝渗透率，所以致密油气藏其实属于双重介质油气藏。本次研究，引用了经典的Warren & Root的双重介质模型[3]。人工压裂缝控制区之外的区域，相当于没有经过压裂的原始致密油藏区域。原始致密油藏区域的渗流主要受基质岩块控制。

本文研究的致密油藏多段压裂水平井模型，根据水力压裂缝的半长xF将致密油藏分为三个区域(图1)：油藏X轴方向上大于xF的区域定义为原始致密油藏区域，或水力压裂缝控制之外的区域；油藏X轴方向上不大于xF的区域定义为水力压裂缝控制的双重介质区域；以及水力压裂缝内部区域。这三个区域的交界面处分别有油藏压力相等，及流量相等的联接条件。在这三个区域中存在着基质、天然裂缝、水力裂缝以及水平井筒之间的复杂渗流。

该模型中，水平井的水平段长度等于D，基本等于最远两条压裂缝之间的距离，单位英尺；水力压裂缝的数目为nF；对于水力压裂缝的缝距，本文假设是相等的，缝距之半等于ye，因此ye=D/(2nF)，单位英尺；水力压裂缝的半长等于xF，单位英尺；水平井筒距离油藏的外边界的距离为xe，相当于两口相邻水平井的水平段距离之半，单位英尺。水力压裂缝的宽度为wF,单位英尺。

边界条件：当两口相邻水平井相互干扰前，它们的中线处xe无流体流动；两条裂缝的中线处ye无流体流动。定义水平井的轴线，水力压裂裂缝的轴线为非流动区域[4]。

图1 致密油藏中多段压裂水平井流体渗流示意图

根据Raghavan和Chen[5-6]的研究，对于n条性质一样的垂直裂缝控制的油藏区域，相当于1条水力压裂缝。这条等效裂缝的半长等于n条垂直裂缝中，距离最远的两条水力压裂缝之间的距离之半；等效裂缝的宽度等于n条垂直裂缝中任意一条裂缝的半长；等效裂缝的高度等于对于n条垂直裂缝中任意一条裂缝的高度。等效裂缝的导流能力C等效是天然裂缝的渗透率kf、天然裂缝宽度wf、基质渗透率km、最远两条水力压裂缝之间距离D的函数，kf和km单位10-3μm2，wf和D单位ft。可以根据Raghavan的公式确定：

(1)

则水力压裂缝控制外的油藏向水力压裂缝控制内油藏的渗流，相当于外部的基质系统向一条等效裂缝的渗流。

对于水力压裂缝控制油藏内的流体渗流，相当于双重介质系统向水力压裂缝的渗流。由于基质岩块的渗透率极低，本文假设其不向水力压裂缝直接渗流。也就是说，水力压裂缝内的油藏主要由天然裂缝向水力压裂缝渗流。且当两条水力压裂缝干扰之前，这种流动形态主要为线性流[7]。

对于水力压裂缝内向水平井筒的流动与垂直压裂井模型一致，水力裂缝内的流动主要还是线性流。当然，井筒与水平井筒的接触面，是一个圆柱体表面。因此在开始阶段的井筒附近，流动类型属于径向流，这就是水平井筒的储集效应。早期的水力裂缝内的径向流持续非常短的时间，对生产的影响不大，因此本文未考虑井筒储集效应的影响。要精确地研究井筒储集效应的影响，可以参考Larsen & Hegre[8]的方法，在模型中加入表皮因子来解决。

1.1 对于裂缝控制外油藏

对于裂缝控制外油藏，相当于求解垂直裂缝稳态解。长方体油藏中，油藏厚度ho，油藏长度为a，宽度为b，单位均为m。该油藏中有一条天然垂直裂缝，裂缝高度等于油藏厚度ho，也就是说天然裂缝穿透致密油藏；裂缝长度Lf。垂直裂缝位于油藏中心。与垂直裂缝平行(假设长度为b)的两侧为恒压边界，压力为pe，裂缝压力为pf,油藏顶、底边界以及与垂直裂缝相垂直的两侧边界为封闭边界[9]。

则垂直天然裂缝处的稳态产能公式为：

(2)

其中：Q为天然裂缝的稳态产能，桶/天；km为基质渗透率，10-3μm2；h为油藏厚度，ft；μo为原油黏度，mPa.s；Bo为原油体积系数，psi-1;pe、pf分别为油藏压力和井底流压，psi。a，b分别为油藏长度和宽度，ft；Lf为天然裂缝的长度，ft。

为了计算简便，我们假设油藏为正方形油藏，且水平井筒的长度等于正方形边长，也就是：a=b=2xe=D。

根据Raghavan的等效裂缝理论，则n条水力压裂缝控制的区域相当于一条等效裂缝。这条等效裂缝的长度Lf等于水平井段的长度D。设等效裂缝的初始压力为Peffi。将式(2)变换可得：

(3)

1.2 对于裂缝控制内油藏

根据物理模型的描述，对于水力压裂缝控制内油藏的渗流，为天然裂缝向水力压裂缝的渗流，n条水力压裂缝将正方形油藏分成n个长方形区域。对n条裂缝中的某一条进行分析，根据范子菲方法同理可以得到：

(4)

上式中的Q″为天然裂缝向某一根水力压裂缝的流量，等于Q′/n；pfi、PFi分别为天然裂缝和水力压裂缝的初始压力，psi。且Pfi等于Peffi。

1.3 对于水力压裂缝内油藏

在裂缝高度等于油藏厚度的情况下，根据Michale[10]的方法，有下式成立：

(5)

上式中Pwfi为井底流压，psi；rw为井筒半径，ft。

综合式(3),(4)和(5)式，致密油藏的多段压裂水平井稳态初始产能公式为：

(6)

2 体积压裂水平井产能影响因素分析

根据以上分析，根据公式(6)进行实例计算，并分析影响压裂水平井产能影响因素分析。原始计算参数参考了某实际致密油藏参数,见表1。

根据表1提供的参数，用(6)式计算，可得多段压裂水平井的初始产量约为200桶/天。该数值比较符合生产实际情况。

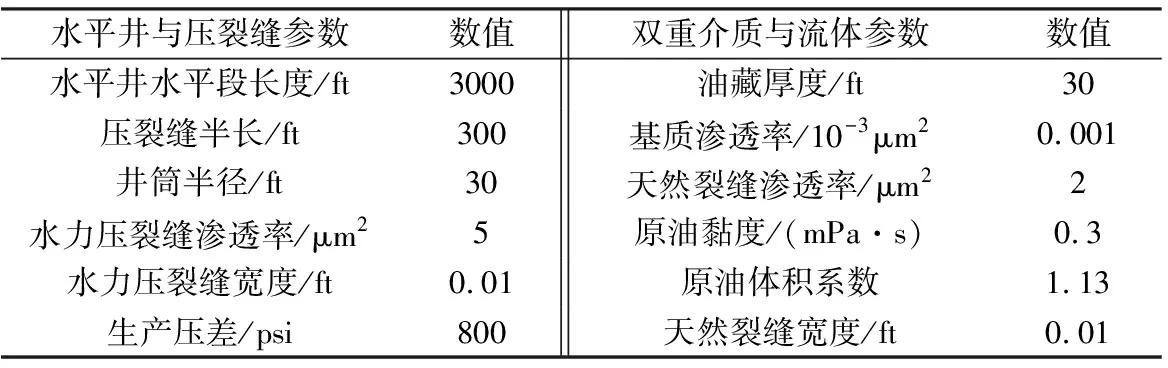
表1 原始计算参数

2.1 压裂缝数量对产能的影响

由图2可知，水平井的初始产量随水力压裂缝的条数增加而增加，当水力压裂缝条数较少时，每增加一条压裂缝的增产效果更明显。

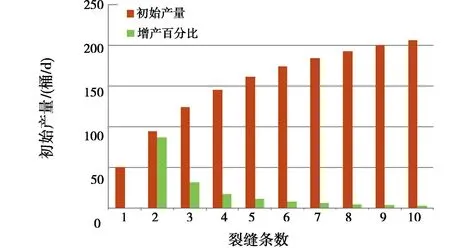
图2 压裂缝条数对产能的影响曲线

2.2 裂缝半长对产能的影响

由图3可知，当其他参数不变，水平井的初始产量随水力压裂缝半长的增加而增加。当水力压裂缝较短时，这种改善效果越好。但是当压裂缝长度增加到一定程度后，这种增产效果变差。

2.3 水平段长度对产能的影响

由图4可知，当其他参数不变，水平井的初始产量随水平段长度的增加而增加。当水平段较短时，增加其长度对产能的改善效果越好。但是当水平段长度增加到一定程度后，这种增产效果变差。水平段长度的增产效果不如增加压裂缝条数的效果。

2.4 导流能力对产能的影响

由图5可知，当其他参数不变，水平井的初始产量随压裂缝导流能力的增加而增加。当压裂缝的导流能力比较小时，通过提高压裂效果增加其导流能力的措施，可以较好的增加水平井产能。但是当导流能力达到0.11μm2后，再提高导流能力，其增产效果不明显。

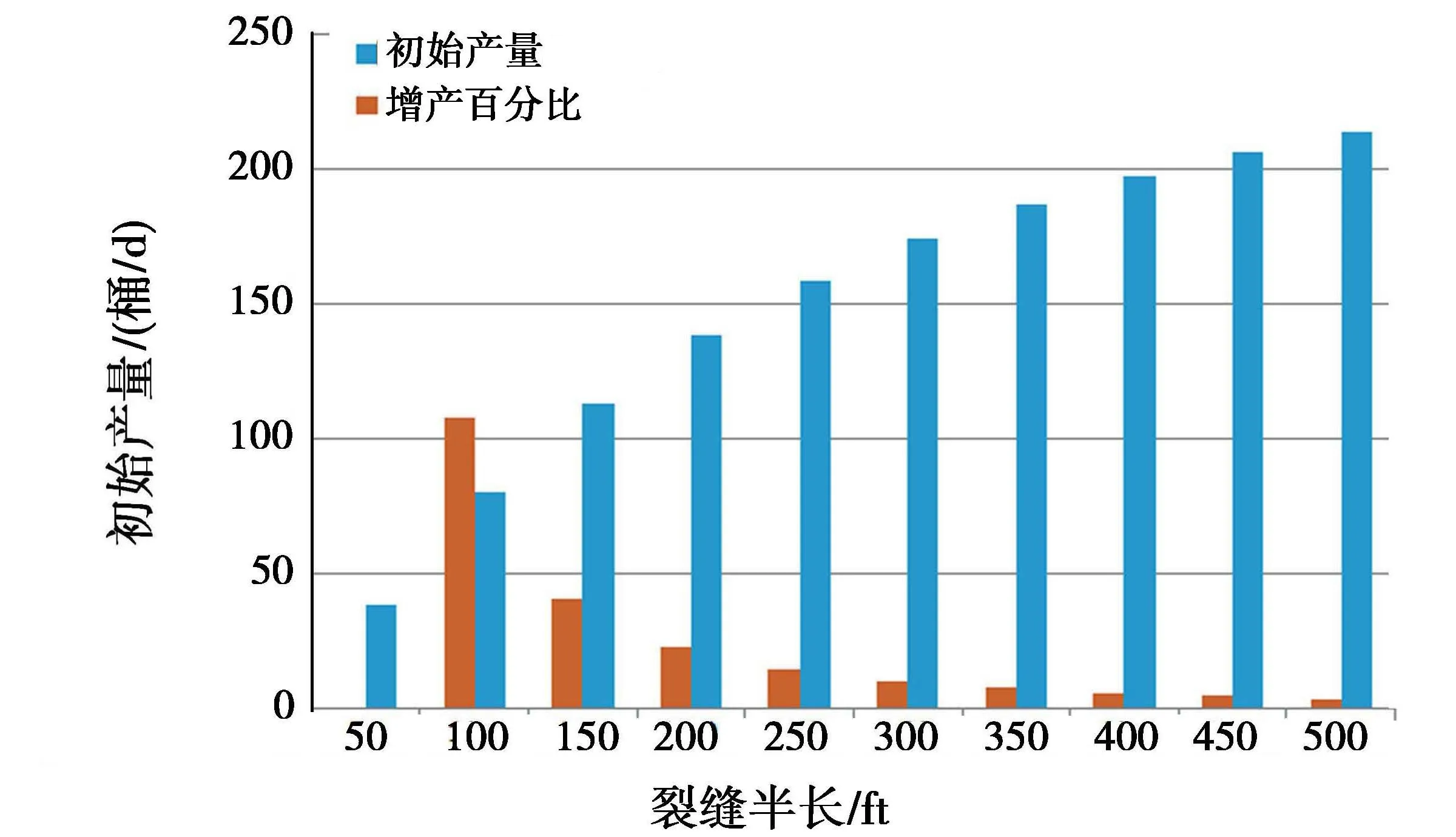
图3 裂缝半长对产能的影响

图4 水平段长度对产能的影响

3 结论

(1)致密油藏表现出双孔介质特征。

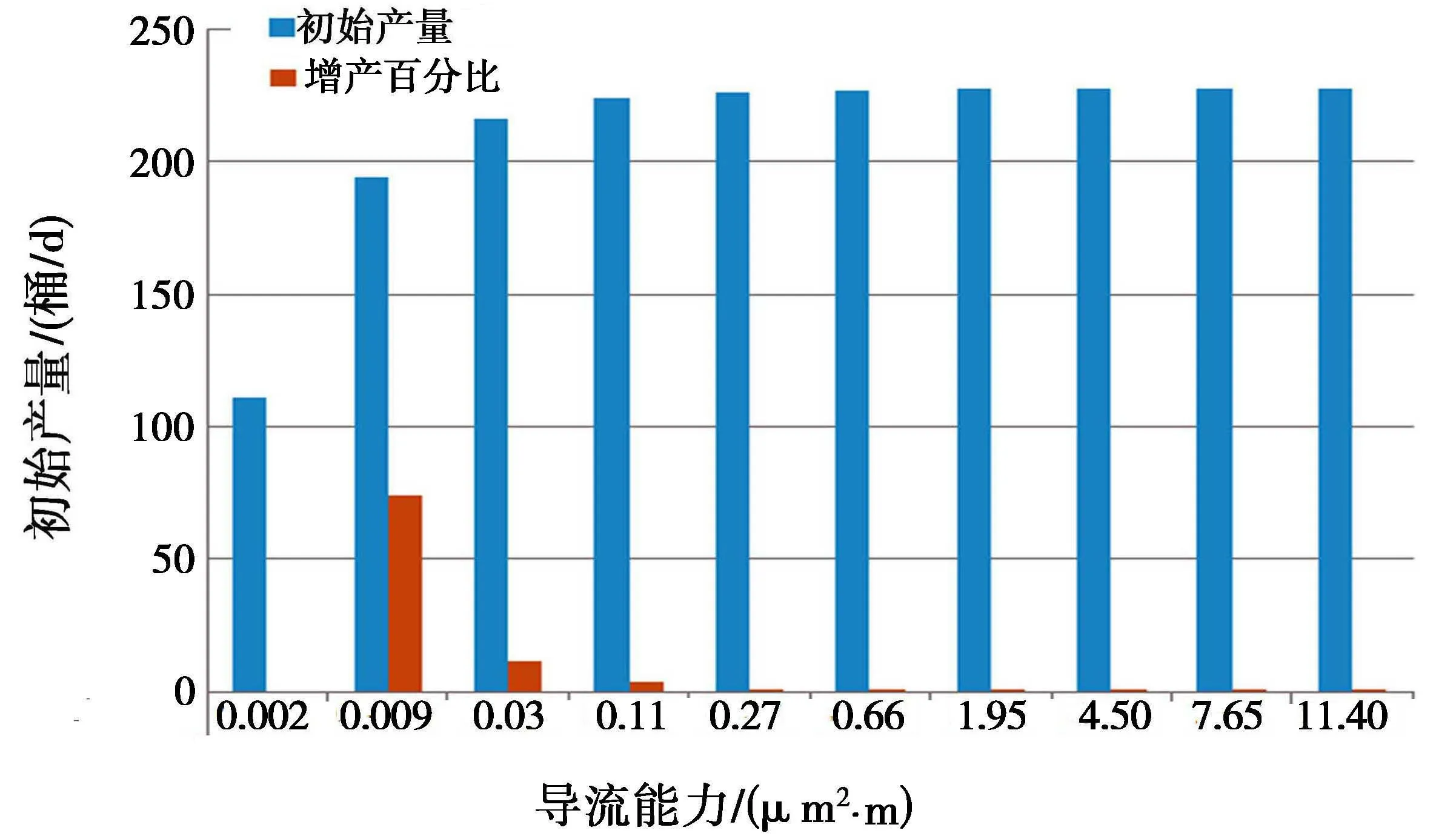
图5 导流能力对产能的影响

(2)将致密油藏划分为三个区域，线性流是压裂水平井中流体主要流动形态,本文建立的体积压裂水平井产能方程，可以近似准确地求解压裂水平井初始产能。

(3)适当增加水力压裂缝的条数、增加压裂缝的半长，有利于激活双重介质的致密油藏中天然微裂缝，从而增加产能。

[1] 苗和平,王鸿勋.水平井压后产量预测及裂缝数优选[J].石油钻采工艺,1992,14(6):51-56.

[2] 李笑萍.穿过多条垂直裂缝的水平井渗流问题及压降曲线[J].石油学报,1996,17(2):91-97.

[3] Warren J E,Root P J.The behavior of naturally fractured reservoirs[J].SPE 1963，3(3):245-255.

[4] Brown M,Ozkan E，Ragahavan R.Practical solutions for pressure transient responses of fractured horizontal wells in unconventional reservoirs[J].SPE 125043 presented at SPE Annual Technical Conference and Exhibition, New Orleans,2009.

[5] Chen C C,Raghavan R. A multiply-fractured horizontal well in a rectangular drainage region[J].SPE,1997,2(4):455-465.

[6] Raghavan R S, Chen C C,Agarwal B. An analysis of horizontal wells intercepted by multiple fractures[J].SPE,2008,2(3):235-245.

[7] 杨俊峰.致密油藏压裂水平井生产动态分析方法[J].石油地质与工程，2013,27(5):85-88.

[8] Larsen L，Hegre T M. Pressure transient analysis of multi-fractured horizontal wells[J].SPE 28389 presented at the SPE Annual Technical Conference and Exhibition, New Orleans,1994.

[9] 范子菲，方宏长.裂缝性油藏水平井稳态解产能公式研究[J].石油勘探与开发,1996,23(3):52-63.

[10] Michale H M. A parametric comparison of horizontal and vertical well performance[J],SPE18303，1998.