基于油冷管失效的振动试验方法的研究
施 杰,贾传林,张 汝,秦 昀,濮龙锋
(1.泛亚汽车技术中心有限公司,上海 201201; 2.苏州广博力学环境实验室有限公司,苏州 215122)
引言
油冷管是连接汽车变速箱到前端油冷器的重要连接管路。管子直接承载变速箱油的换热工作,管内工作介质是变速箱润滑油,其温度和压力可达150摄氏度和350Kpa。油冷管结构如图1所示,AEM橡胶和钢管压接,与变速箱连接处钢管与铝制压板镦压成型,与水箱的油冷器连接处通过快速接头方式进行连接。
油冷管在整车的激振环境条件下造成的泄漏是主要失效模式。由于变速箱所处位置靠近发动机动力输出源,因此油冷管变速箱连接一侧接口处的油泄是经常出现的。由以上分析可得,以实车的振动路谱来修正台架试验标准是必要的。
综合以往文献,刘洋、胡善清等在多通道高速数据采集系统设计中采用TS201处理芯片从硬件设计和软件设计两方面详细讨论了多通道高速数据采集以及高速数据预处理的设计与实现;彭思达、纪昌春、蒋永、仇春强在发动机低频振动信号采集系统设计与实现中分析了发动机稳定怠速工况(750 ± 100r/min)低频的振动信号特点;蔡巍巍、汤宝平、黄庆卿在面向机械振动信号采集的无线传感器网络节点设计中尝试采用新型微机电系统(MEMS: Micro-Electro-Mechanical Systems),利用加速度传感器采集振动信号并且选用了2.4GHz 频段的低功耗无线射频芯片CC2430作为无线通讯模块;高安生、阎菲在多路振动信号采集与处理系统的研究中,介绍了微机控制液压振动试验台研制过程中多路振动信号采集与处理方法;孙启甲在实车空调系统异响诊断技术研究中提出了频响函数路径共振验证,通过阶次分析共振来确认诊断位置。

图1 油冷管走向和连接形式
本文基于M公司B型油冷管的失效现象,采集了实际道路负荷,采用快速傅立叶变换成频域信号,找到接近共振点能量,修订台架试验的随机振动扫频曲线,使得失效模式得到良好的复现。
1 产品失效模式与理论分析
如图2所示,是经过M公司整车高速路试的结果,油冷管在变速箱一侧,出现油冷管镦压位置出现泄漏(通过保压水检方法),见剖解图3中明显显示镦压位置内侧出现裂纹,这里属于变速箱油进口位置。
循环的外部载荷是引起试验样件应变疲劳的主要原因。图3的失效模式可以近似为拉伸应力所造成的,其应力计算为:
σ= P/A

图2 泄漏位置和剖解结果

图3 剖解放大图
其中:P为所施加的载荷;A 为试件变形后的横截面积。
如上式所示,随着载荷的增加,材料进入屈服,经过强化直至最后的断裂。
载荷从0到P的过程,试件拉伸变形是逐渐的,应变的增量dε等于长度增量dl和变形后长度l之比:
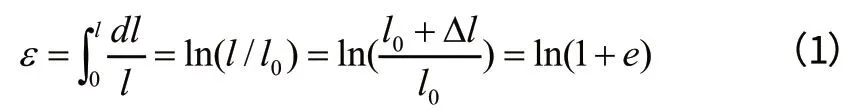
忽略弹性体变形,假设发生变形后体积不变,则有:

因此应变公式又可以写为:
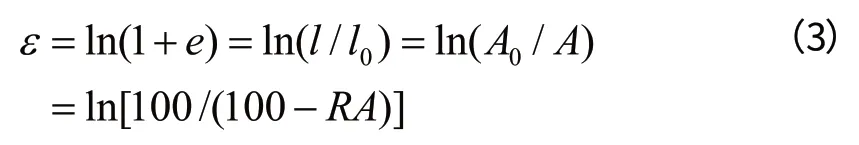
当考虑弹性变形时,总的应变应该是弹性应变εe和塑性应变εp之和。值得注意的是随着外力卸载,弹性变形是可以恢复的,而塑性应变作为应变残余留在试件中。
弹性应力根据虎克定律:

塑性应力根据holomon关系式:

式中,K为强度系数;n为应变指数,无量纲。
因此应力和应变关系可写为下式:
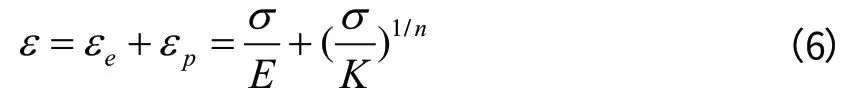
因此应力的大小直接关系到最后失效位置和时间历程。对于工作状态的油冷管,其受力主要部分是管内工作介质润滑油的流动压力。据以往数据,常见内压可达300kpa左右,本身力的基数就不大,此外由于油冷管总成有1/3长度是AEM胶管,可以吸收大部分管内的压力或者压力脉动。因此外部振动激励使得油管尤其在连接处的应力集中最终造成油管的管体破损。
由于是在道路试验的高速环路工况下发现的油管泄漏现象,因此路面的影响不明显。而油冷管的失效位置是靠近发动机的一侧,所以本文主要针对路试结果研究了发动机激励的影响。
常用的实际道路信号主要有位移信号和加速度信号,尤其以加速度信号的时域谱收集最为常见,位移信号主要是研究危害程度以及进行失效分析。此外台架的试验主要采用随机振动来验定特定激振谱条件下产品的抗振性能,因此本文以加速度信号采集为主来进行研究。加速度作用的效果可以用损伤公式表示,如下式:

其中:T为试验时间或者加载时间;Grms为随机振动谱的平均加速度;n为寿命系数,一般机械应力取在4~6之间。
2 路谱分析和台架转化
本文依据失效油冷管所在的车舱内的安装位置,在油冷管靠近变速箱进出口的连接块上布置了两个加速度传感器,并进行了三向加速度时域数据信号采集。
这样在台架振动控制中,可以比较真实地反映到油冷管的振动实际情况,同时可以得到准确和平稳的振动台体反馈信号。如图4所示,左侧是进口管加速度传感器位置,右侧是出口管加速度传感器位置。
一般时域信号需要转化为频域信号来进行分析,对于一个N点离散序列f(n),其离散傅立叶变换对其定义为:


图4 加速度传感器位置

1965年Cooley和Tukey发表了有关快速傅立叶变换的著名论文,使离散傅立叶变换的运算量大大下降。图基-库利(Cooley-Tukey)算法的基本思想是把一个N点长序列f(n)按照奇、偶分解成两个短序列f1(k)和f2(k),分别求出短序列的离散傅立叶变换结果F1(k)和F2(k)。f(n)的离散傅立叶变换结果按照如下的关系线性组合:

式中,k的取值范围为0—N/2-1。
这样就把常规的N2级别的计算量大大缩减。
本文利用了图基-库利(Cooley-Tukey)算法转化时域信号,通过对比发现发动机2500转时油冷管运动出现较大的加速度。如图5、6是出口管位置和进口管位置两个加速度传感器的频域数据。
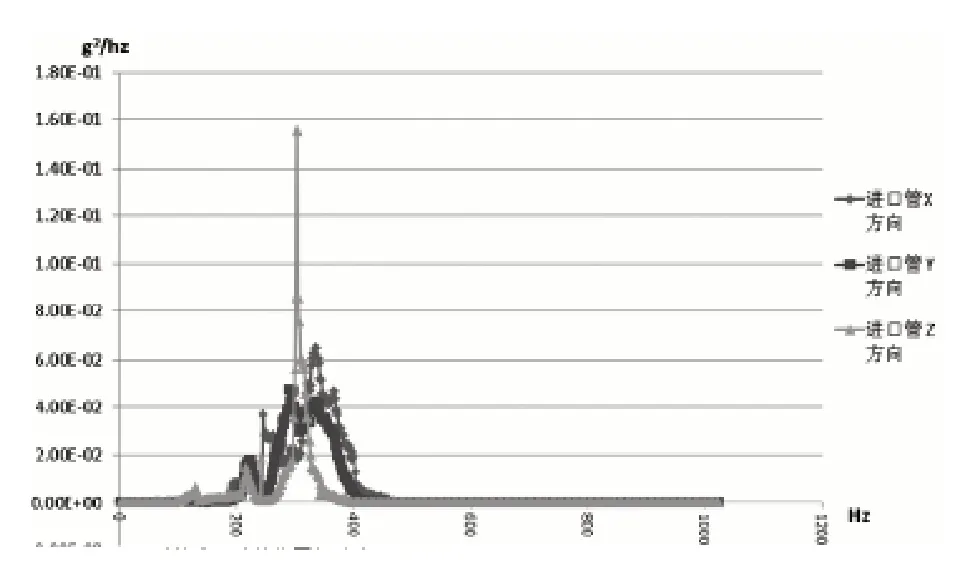
图5 2500rpm 时的进口油管位置加速度PSD
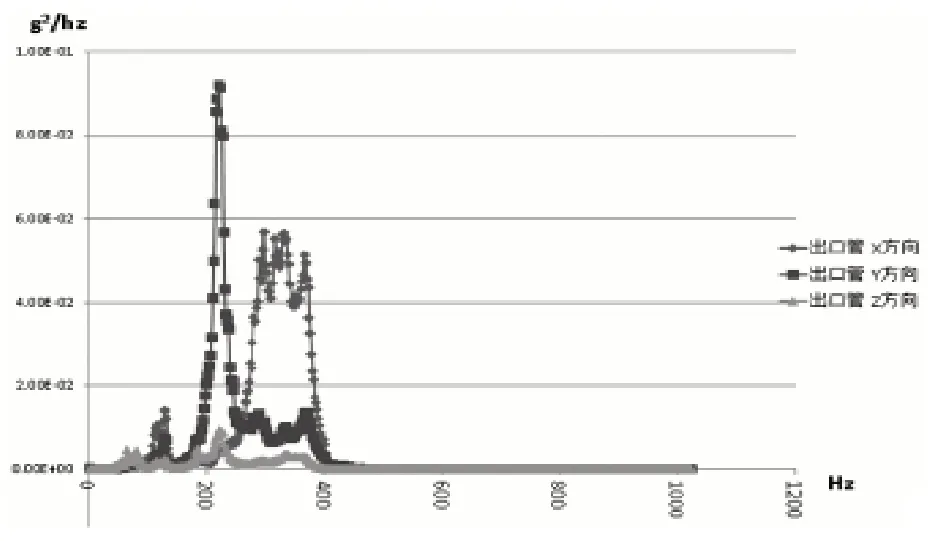
图6 2500rpm 时的出口油管位置加速度PSD
从进口管位置的PSD谱型看到,加速度峰值出现在304Hz,单点峰值功率谱密度是0.16g2/Hz,大概是激振源转速即发动机转速2500rpm的7倍谐波。能量分布来看Z方向的功率谱密度最大 ,Y方向最小。从图5可知在200Hz到400Hz范围内,能量比较集中,振动剧烈。
从出口管位置的PSD谱型看到,加速度峰值出现在224Hz,单点功率谱密度是0.09g2/Hz,大概是激振源转速即发动机转速2500rpm的5倍谐波。能量分布来看Y方向的功率谱密度最大 ,Z方向最小。从图6可知在200Hz到400Hz范围内,能量比较集中,振动剧烈。
所以出现失效的进口管位置能量在z方向比较大,这是主要的失效诱因。并且依据管路在200Hz到400Hz范围内能量集中的特点,有必要修正原M企业针对油冷管台架振动的试验频谱(此前按照标准谱的台架振动试验并没有振出问题)。随机振动路谱能量大小是计算其GRMS即PSD频域线下的包络面积。
GRMS的计算如下式所示:
Grms=sqrt(areaA+areaB +areaC+areaD)
在100Hz到300Hz条件下原有谱单点0.05g2/Hz能量不足以代表实车状态,因此需要进行修正如下表。表中增加了315Hz频域点,并且提升功率谱密度,从0.05 g2/Hz提升到0.16g2/Hz。
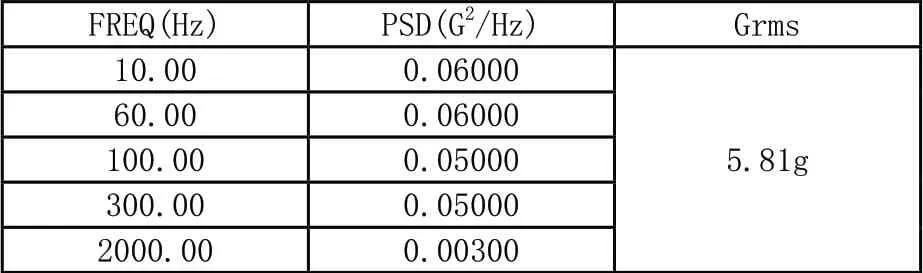
表1 M 公司随机振动谱和GRMS 计算结果
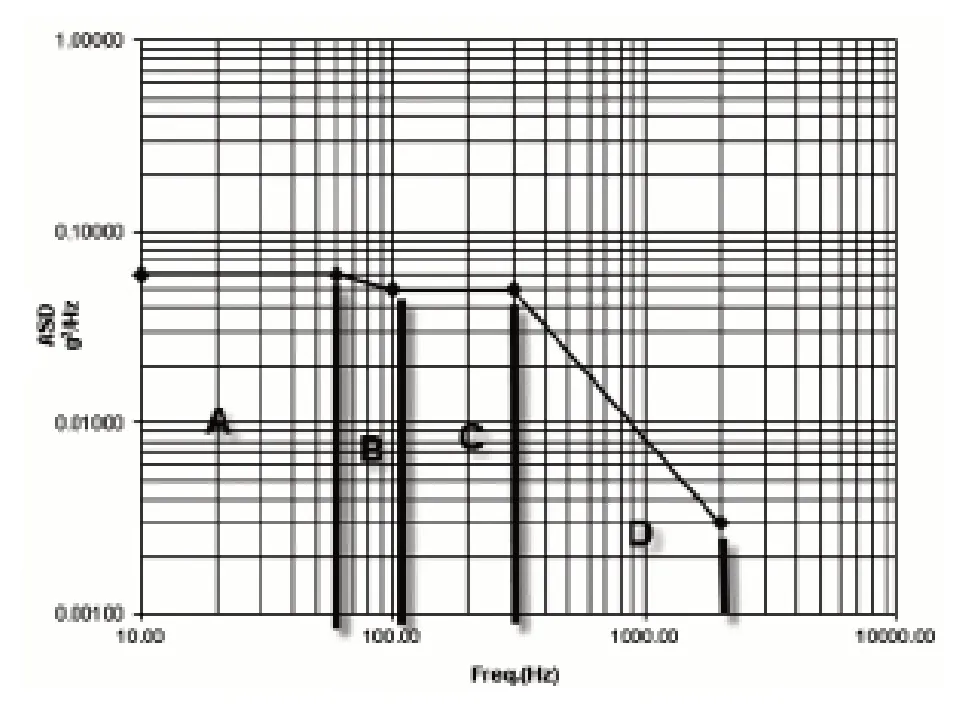
图7 M 公司油冷管振动标准频谱的对数坐标系显示
试验时间和步骤仍按照老的试验标准, 上下、水平、前后三个方向顺次试验,每个方向22h。
3 台架搭建和新谱随机扫频试验
本文使用电磁振动台参数: 型号为某公司DC-3200电磁振动试验系统,其额定激振力为3.2kN,额定位移为51mm p-p,额定速度为2m/s,额定加速度为100g,额定频率范围为5Hz~2000Hz。如图9是工装搭建。工装分为两部分,产品按照实车走向,靠近变速箱一侧固定工装固定在电磁振动台面,水箱快速接头一侧的固定工装固搭在地面上,以突出油冷管两侧位移差。进出试验油管预装满润滑油。如图10是实际台架布置。
反馈信号加速度传感器按照道路数采位置固定在变速箱进出口支架旁如图9,台架扫频信号控制如图11。台体振动输出曲线均在控制上下极限范围内,台架试验控制稳定。

表2 修正后的随机振动谱和GRMS 计算结果
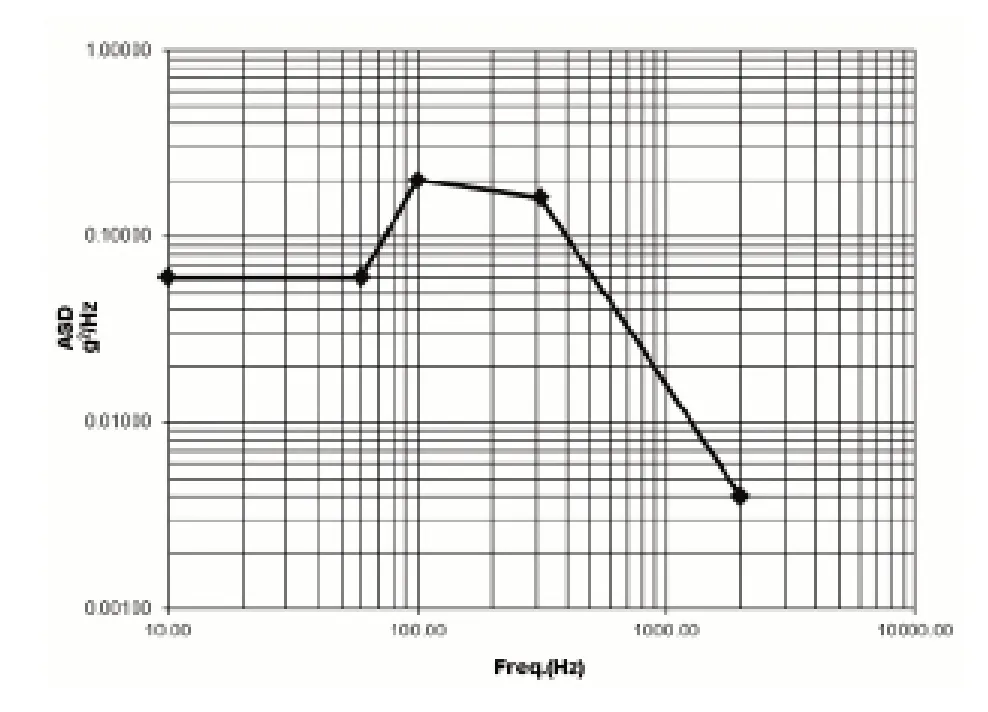
图8 修正后的频谱PSD

图9 台架控制加速度传感器位置

图10 实际台架布置

图11 台体随机振动扫频输出曲线
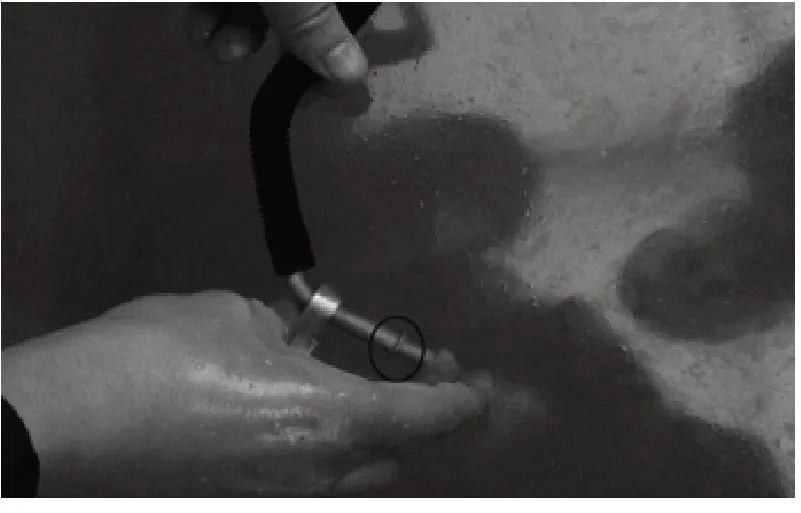
图12 新谱振动后样件失效位置水检情况
试验结果:按照新谱,同批次样件在试验完成z方向阶段的第16h振动时发生油泄露,占试验进程24.2%,而同批次油冷管在整车道路试验失效点在21%左右。
将泄露的进口管油倒出,通入200kpa氮气浸没在水中水检。如图12看到油管泄露冒泡位置和实车失效样件近似,证明新谱的有效性和可行性。
4 结论
通过以上的设计计算分析,可以得到如下结论:
1)本文分析了车用油冷管的主要失效形式和失效机理,并比较了弹性应变和塑性应变的影响。
2)讨论了实际道路的时域谱向频域谱的转化方法,运用快速傅立叶变换可以很好保证谱型不失真,并减少计算的工作量。
3)关注实车频域谱中的峰值点和能量集中区域,其对台架PSD的修正至为关键。
4)搭建了相关工装台架,采用多自由度安装实现实车载荷效果。
[1]高安生,阎菲. 多路震动信号采集与处理系统的研制[J].湖北汽车工业学院学报,1993,2.
[2]胡刘洋,胡善清,龙腾.多通道高速数据采集系统设计[J]. 计算机工程与应用,2012,48(S2).
[3]彭思达,纪昌春,蒋永,仇春强.发动机低频振动信号采集系统设计与实现[J].自动化技术与应用,2010,29(1).
[4]朱家富.傅立叶变换在工程应用中的演变[J].重庆文理学院学报,2009,28(1).
[5]蔡巍巍,汤宝平,黄庆卿.面向机械振动信号采集的无线传感器网络节点设计[J].振动与冲击,2013,32(1).
[6]Cooley JW, Tukey JW. An algorithm for the machine calculation of complex Fourier series[J]. Mathematics Computation, 1965, 19(4): 296-301.
[7]陈长征,胡立新.设备振动分析与故障诊断技术[M].北京:技术科学出版社, 2007.5.

