大展弦比机翼几何非线性气动弹性响应分析

许 成,员海玮

(南京航空航天大学 航空宇航学院，江苏 南京 210016)

高空长航时无人机可昼夜长时间巡航，执行空中侦察、监控、科研探测等任务，具有广阔的应用前景。该类飞机一般采用大展弦比机翼结构，在气动力作用下机翼变形明显，几何非线性特征显著，非线性气动弹性分析技术成为研究该类结构气动弹性问题的有效工具。

在几何非线性气动弹性问题的研究方面，Tang和Dowell[1]以线性化的方法对简化的梁模型进行非线性颤振分析，结果与实验值吻合良好，表明该方法可以较好的预估颤振发生时的速度。谢长川、杨超[2，3]等人借助动力学线化的方式，对大展弦比机翼展开气动弹性稳定性分析，与线性分析结果对比表明，由于几何非线性的影响，线性颤振计算方法不能准确地预测临界颤振速度。

除采取分步线化方法实现非线性气动弹性分析之外，也可采用非线性气动响应方法进行气动弹性响应分析。冉玉国等[4]通过修改NASTRAN软件求解序列，在非线性瞬态响应求解模块中引入气动力计算模块，成功实现了非线性气动弹性响应分析功能。崔鹏、韩景龙等[5]利用CFD/CSD方法，对切尖三角翼模型进行非线性颤振研究，相对于实验结果，取得了良好的计算精度。

虽然CFD/CSD的方法是一种精确的方法，然而CFD方法计算量巨大，效率较低，本文尝试采用拟合气动力与高精度动响应求解器结合的方法，建立起一套求解方法，以实现对几何非线性气动弹性响应问题的高效求解。

1 气动弹性响应分析

1.1 非线性有限元列式及动响应求解

本文构造一种厚薄通用的四边形板壳单元作为有限元建模的基本单元。该单元由板元、膜元两部分组合而成。其中，板元部分通过合理假设剪切应变场的方式避免出现剪切闭锁现象[6]；膜元部分以Allman型二次膜位移插值模式为参考[7]，将面内位移场写成双线性协调函数与节点旋转自由度确定的高次位移场之和的形式[8]，不仅提高了单元性能，而且增加了一法向转动自由度。

图1 节点自由度的定义Fig.1 Definition of node DOF

根据Mindlin板理论及von Karman大挠度理论，将壳元对应的Green应变写成线性与非线性之和形式：

(1)

将上式拆散记为：

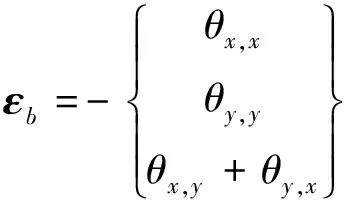
(2)

其中εm、εb和εs分别表示单元的膜应变、弯扭应变和剪切应变。

根据式(1)，按照标准有限元推导过程，可得单元的几何矩阵为：

B=B0+Bl

(3)

其中，线性部分B0=[BmBbBs]T，非线性部分Bl=AG=A[G1G2G3G4]。

在以上两式中：

Bm=[Bm1Bm2Bm3Bm4]

(4)

Bb=[Bb1Bb2Bb3Bb4]

(5)

(6)

为了避免板壳单元在用于薄板分析时出现的剪切闭锁现象[8]，此处重新假设剪切应变场，经过修正，板壳单元的剪应变几何矩阵表示为：

(7)

应用时只需将B0中的Bs替换掉即可，其中Ns、Xs、Ys和Γ*在文献[6,7]中已详细给出。

动响应计算过程中，采用修正的UL方法进行时间步推进，即在每一时间步开始时刻进行参考构型更新，由于时间步内部迭代参考构型不变，所以时间步内部应力可直接叠加，记S为Kirchhoff应力：

S(k+1)=S(k)+△S

(8)

其中，D为组集后的弹性矩阵，△q为结构节点位移增量。

每次时间推进时，首先要将Kirchhoff应力转换为Cauchy应力。

在Mindlin板假设与大变形情形下，板单元的切线刚阵由单元线性刚阵、初位移刚阵和初应力刚阵组成，形式如下[8]：

(9)

将单元的切线刚度矩阵组集为整体切线刚度矩阵，代入系统的动力学方程：

(10)

采用Newmark方法内部嵌套Newton-Raphon迭代的方式，求解上述非线性动力方程组[9]，将上式改写为等效静力形式：

Keff△u=Peff

(11)

其中，Keff、Peff分别为有效切线刚阵、有效不平衡力，R为外载荷，F为节点等效内力。

1.2 非定常气动力的时域耦合

对于高空长航时无人飞行器来说，由于其巡航速度一般处于亚音速范围，机翼所受的气动力可视为线性气动力，并且可忽略非定常气动力的非平面效应，从而可以选用偶极子格网法计算其频域下的非定常气动力，再利用有理函数拟合转换到时域表达。 作用在结构有限元模型上的气动力表达式可记为：

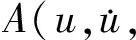
(12)

(13)

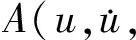
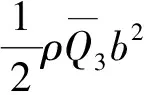
(14)

其中：

yi(t+△t)=

i=1,2,3,4

(15)

至此，气动力表达式完全转化到时域。

1.3 流固紧耦合实现

采用紧耦合方式在时域下对气动力、结构动力学方程分别求解，在每一时间步内固结迭代，直到结构变形与气动力变化到达平衡状态，再解除时间步固结，向下一时间步推进。时间步的推进分为真实推进(解除时间步固结后的推进)和假想推进(固结的时间步内部假想的推进)，具体的计算过程如下：

(1)初始化气动力求解系统，给定滞后项和实系数矩阵，给出初始y值；

(3)求解tn(m)(tn时刻的第m次配平迭代)时刻气动力向量Qn(m)(m=0,1,2,…)；

(4)将求得的气动力向量Qn(m)传递到结构响应系统，将结构响应求解推进到tn(m+1)时刻；

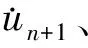
简要计算流程：

图2 程序流程简图Fig.2 Flowchart of the program

2 算例

算例模型为一大展弦比机翼，选取NACA0012翼型，机翼的结构有限元模型如图3所示，机翼根部固支，半展长为2.97 m，平均弦长0.594 m，展弦比为10。在翼稍后缘结点作用一瞬态激励，时间为0.01 s，大小为100 N，响应分析时间步长选取0.001 s。

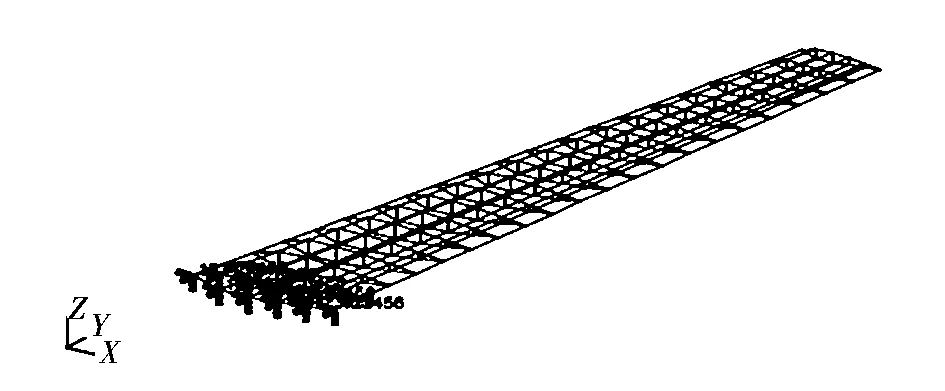
图3 机翼结构的有限元模型Fig.3 The FEM model of wing

模态频率/Hz一阶7.16二阶26.31三阶39.761

分别以本文的气弹响应计算方法与传统的Nastran颤振分析方法对上例进行线性颤振分析。使用本文方法时，主体流程不变，在生成单元刚度时不考虑非线性项，即可对机翼模型做线性气动弹性响应计算。

图4为翼端节点在不同飞行速度时的线性响应。对比线性气弹响应的结果与Nastran颤振分析的计算结果(图5)可见，所得颤振速度几乎相同，可见本文方法具有良好的工程适用性。

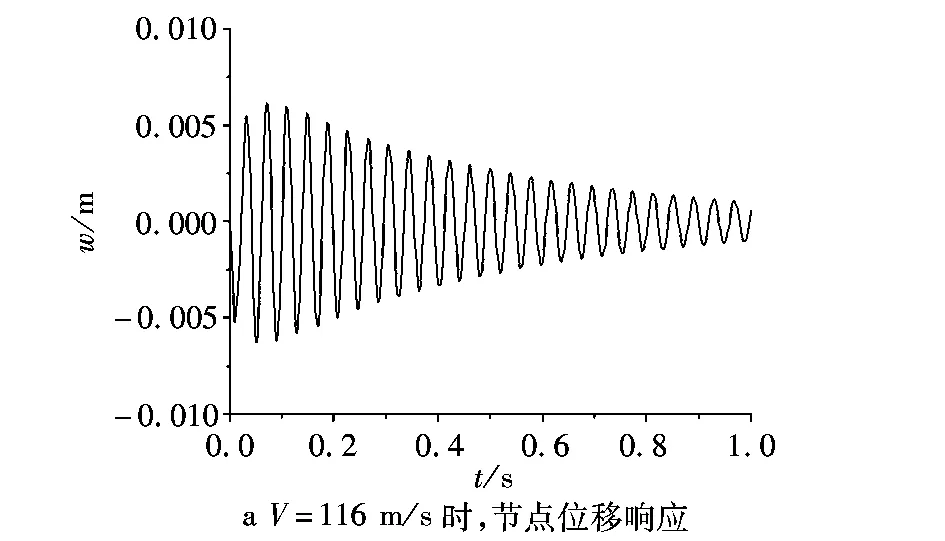
图4 翼端节点在不同飞行速度时的线性响应Fig.4 The liner responses of tip trailing point at certain velocities

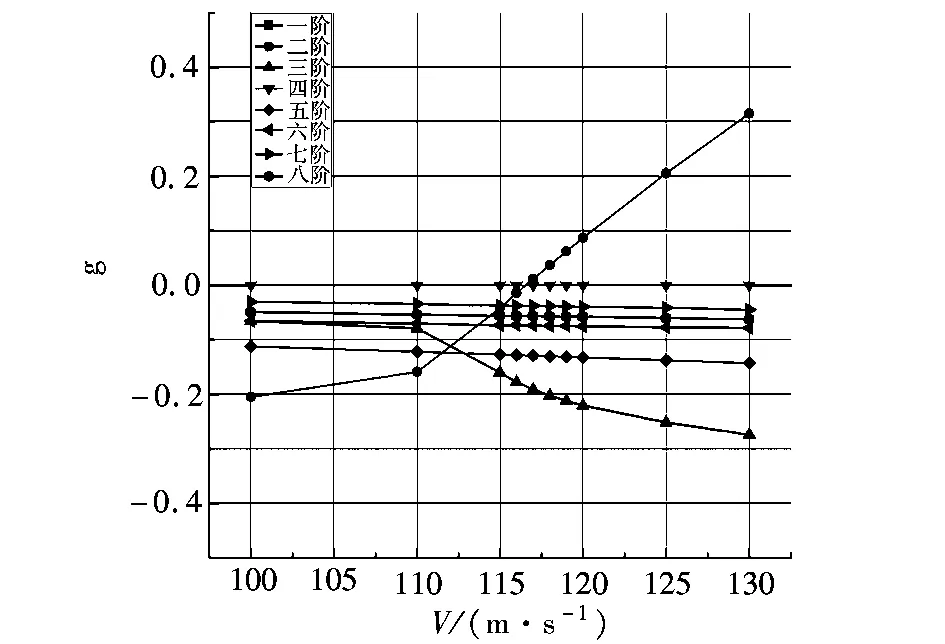
图5 Nastran颤振分析结果Fig.5 The result of Nastran flutter anlysis

仍然采用本文方法，在生成单元刚阵时考虑非线性项，算例不变，在翼端后缘结点作用瞬态激励，时间为0.01 s，大小为100 N，翼端后缘节点位移响应如图6。

在来流速度不变(V=120 m/s)的情况下，给出不同大小的初始激振力f，翼端后缘点位移响应结果如图7。

由图6可见，在给定来流速度的条件下，非线性气动弹性响应幅值逐渐增大，在几何非线性的作用下，响应幅值逐渐稳定，最终做等幅振荡，系统出现极限环振荡现象。来流速度越大，其稳态振荡幅值越大，且随着来流速度的增加，系统进入极限环响应的时间越来越短。另外，在来流速度不变，初始扰动不同的情况下，非线性气动弹性响应幅值从不同的初始扰动出发，最终会回到相同的等幅振荡状态，如图7所示。可见，极限环响应的稳态幅值与系统的初始扰动无关。

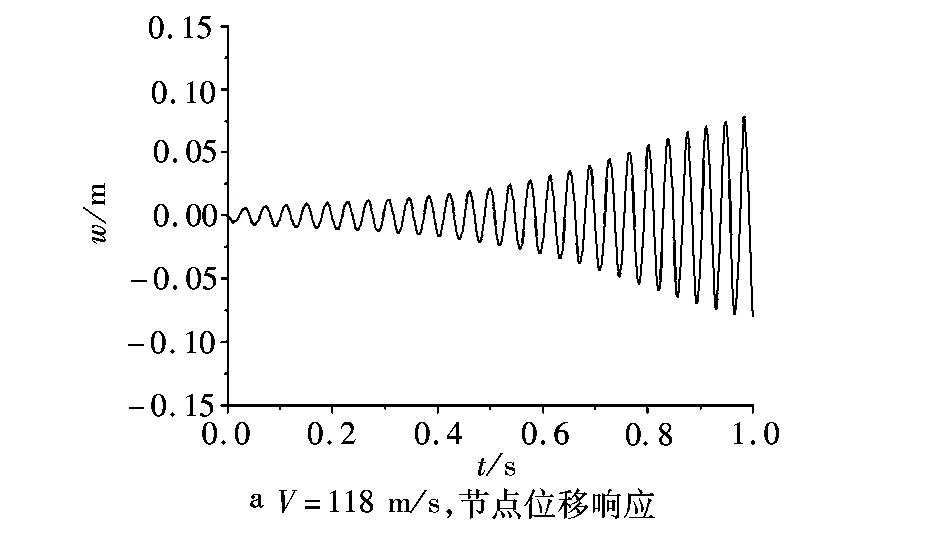
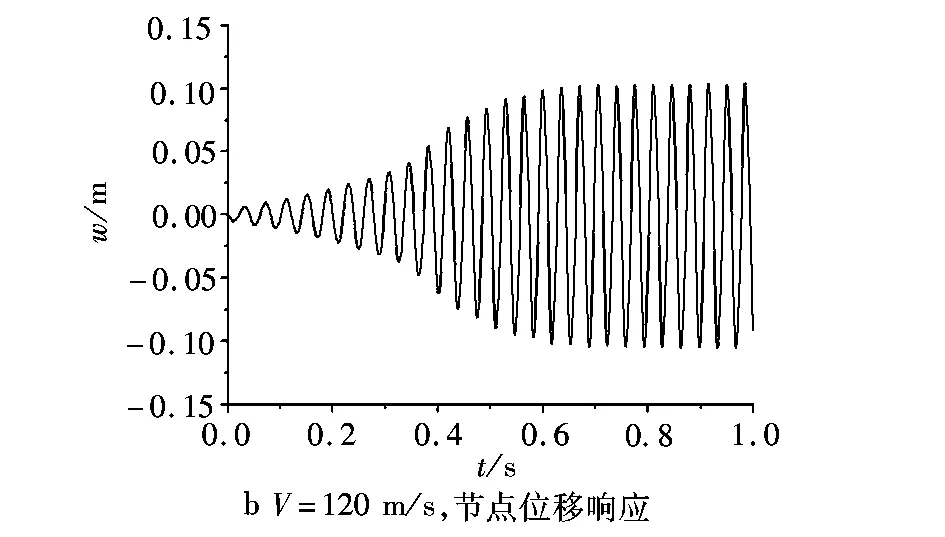
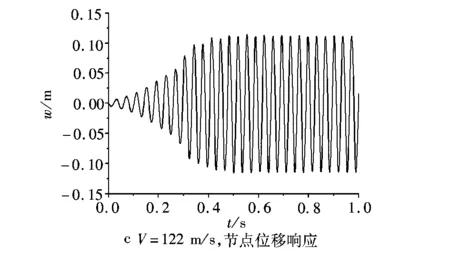
图6 翼端节点在不同飞行速度时的非线性响应Fig.6 The noliner responses of tip trailing point at certain velocities

3 结论

本文借助Nastran软件求解并导出非定常气动力影响系数，通过Roger拟合，得到时域下的非定常气动力，并利用非线性有限元编程，采用紧耦合的方式将非定常气动力加载到结构上，实现了大展弦比机翼的非线性气动弹性响应计算。结果表明，本文提出的方法可有效预测机翼颤振的临界速度。考虑几何非线性影响时，机翼的非线性气动弹性响应系统会发生极限环振荡现象，其振荡幅值与来流速度有关，与初始状态无关。

图7 翼端节点在不同初始状态下的非线性响应Fig.7 The noliner responses of tip trailing point at certain initial state

参考文献：

[1] Tang D, Dowell E H. Experimental and theoretical study on aeroelastic response of high-aspect-ratio wings[J].AIAA journal, 2001,39(8):1 430-1 441.

[2] Xie C C, Leng J Z, Yang C. Geometrical nonlinear aeroelastic stability analysis of a composite high-aspect-ratio wing[J].Shock and Vibration, 2008,15(3):325-333.

[3] 谢长川,杨超.大展弦比飞机几何非线性气动弹性稳定性的线性化方法[J].中国科学: 技术科学,2011,41(3):385-393.

[4] 冉玉国,刘会,韩景龙.大展弦比机翼的非线性气动弹性响应分析[J].空气动力学学报,2009,27(4):394-399.

[5] 崔鹏,韩景龙.基于 CFD/CSD 的非线性气动弹性分析方法[J].航空学报,2010,31(3):480-486.

[6] 岑松,龙志飞.对转角场和剪应变场进行合理插值的厚薄板通用四边形单元[J].工程力学,1999,16(4):1-15.

[7] Ibrahimbegovic A. A novel membrane finite element with an enhanced displacement interpolation[J].Finite elements in analysis and design, 1990,7(2):167-179.

[8] 朱菊芬,郑罡.带旋转自由度C°类任意四边形板 (壳) 单元[J].计算力学学报,2000,17(3):287-292,300.

[9] Bathe K J, Cimento A P. Some practical procedures for the solution of nonlinear finite element equations[J].Computer Methods in Applied Mechanics and Engineering, 1980,22(1):59-85.