自然数方幂和公式的一种新推法
朴元俊, 廉晓龙
( 延边大学师范分院, 吉林 延吉 133000 )
求自然数方幂和既是一个古典的数学问题,也是当今数学研究的热点问题之一.文献[1-5]的作者分别采用逐差法、贝努利数的性质、递推方法等得到了许多有益的研究结果,但其推导过程和结果较为复杂.本文利用组合数学中的母函数理论[6]和排列组合知识,用相对简捷的方法推导出一种比较新颖的自然数方幂和公式.
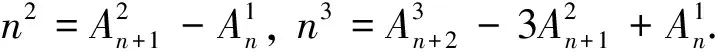
1 预备定理及其证明



(1)
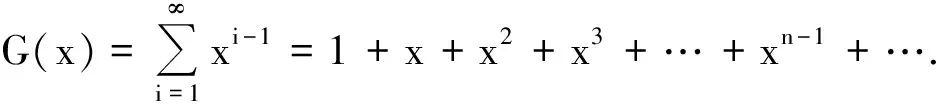


(2)
则系数(Ti j)有递推关系:
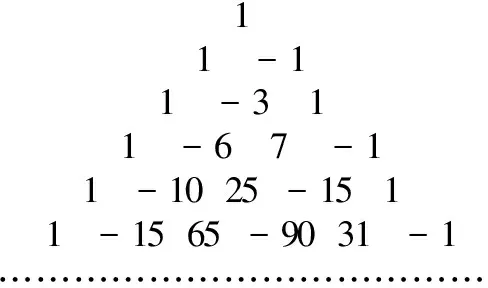
Ti j=-(i-j+1)Ti-1 j-1+Ti-1 j, 1 (3) T22=-T11=-1; T32=-2T21+T22=-3,T33=-T22=1; …. (4) 由(2)式和(4)式,得递推关系Ti j=-(i-j+1)Ti-1 j-1+Ti-1 j, 1 将方幂ni(i∈N)的系数(Ti j)逐次排列成图1所示的“金字塔”形,不难发现:在类似于杨辉三角的“金字塔三角形”状态排列中,每个数都是整数,Ti j表示第i行第j个数(i代表行号,j代表排列序号);从第2行起,每一行数的“符号”交替变换,奇数行的首位数和末数都是1,偶数行的首位数是1、末位数是-1,其他每个数都等于它的左上方的数的相反数乘以自己的倒数序号加上右上方的数.依据递推关系(3),整个“金字塔三角形”图表可以继续写下去.本文称此图表为“类杨辉三角”. 11-11-311-67-11-1025-1511-1565-9031-1………………………………… 图1类杨辉三角 根据定理2的意义,自然数方幂为 则自然数的k次方幂和(数列{nk}的前n项和)为 (5) 基于系数图表(类杨辉三角)的上述求自然数方幂和的公式,仅利用初等排列组合计算即可,这既简捷、新颖,又便于实现计算机编程. 解由(5)式可知: 参考文献: [1] 杨志强.用逐差法求解自然数方幂之和[J].数学的实践与认识,2003,33(11):136-137. [2] 沈明鸣.关于自然数K次幂和的讨论[J].宁波高等专科学校学报,2003,15(4):12-15. [3] 王维芳.自然数次方幂和的一种简捷算法[J].数学教学研究,2008,27(5):49-50. [4] 朱伟义.有关自然数方幂和公式系数的一个新的递推公式[J].数学的实践与认识,2004,34(10):170-173. [5] 朴元俊,廉晓龙.求自然数幂和的一种新方法[J].中国校外教育,2014(4):120. [6] 田秋成.组合数学[M].北京:电子工业出版社,2006.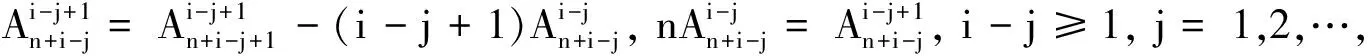



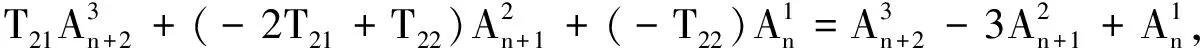
2 主要公式的推导

3 实例


