基于联合稀疏描述的多姿态三维人脸识别

郭哲, 樊养余, 雷涛, 刘姝

(西北工业大学 电子信息学院, 陕西 西安 710072)

基于三维信息的人脸识别,能够从本质上克服二维图像无法避免的对光照、姿态、化妆影响较大的问题[1],成为近年学术界的研究热点。目前的人脸识别方法主要关注基于单个测试数据的识别问题,虽然三维数据能够克服姿态的影响,但是在实际采集过程中,由于人脸姿态的变化,容易导致数据遮挡和缺失,因此会造成数据的不可靠性。为了解决该问题,学者提出采用多个不同姿态人脸数据的联合来完成识别,以提高识别系统对姿态变化的鲁棒性。

在二维人脸识别领域,目前已经公开发表了一系列采用多幅测试图像完成识别的方法[2-5],其中最著名是相互子空间算法(mutual subspace method, MSM)[5],该方法将人脸集建模为Grassmann流形空间[6]中的一个点,因此将集合对集合的距离比较转换为在Grassmann流形中点对点的距离比较。基于稀疏表示的识别方法(sparse representation-based classification, SRC)[7]在2009年提出之后,迅速引起了全世界学者的广泛关注。稀疏表示将人脸识别问题看作多个线性回归模型的分类问题,通过稀疏信号表示理论解决该分类问题,稀疏表示方法已被证明对光照和自遮挡更鲁棒[7]。由于传统稀疏表示的方法仅能处理二维图像的识别问题,Li等人[8]、Guo等人[9]、Tang等人[10]将稀疏表示引入到三维人脸数据识别中。

本文基于二维稀疏表示识别方法,提出了一种用于多姿态三维人脸的联合稀疏描述识别方法(joint sparse representation-based classification, JSRC),该方法能够充分利用所有视图的相互关系,通过建立联合稀疏描述模型进行人脸分类,因此能够用于多幅测试样本的分类问题。JSRC方法假设多幅测试样本共享同一种稀疏类型,利用所有视图的相互关系,联合每一个视图的信息,在联合稀疏重建过程中进行判别区分,从而完成待识别个体的身份判别。该操作能够避免单独对待每一个观测值时所潜在的错误判别风险[11-12],大大提高识别准确率。在国际公开三维人脸数据库FRGC2.0上将本文提出的方法与相互子空间方法和稀疏表示识别方法进行对比,验证了本文方法对多姿态人脸识别的有效性。

1 稀疏表示人脸识别

Wright等人[7]于2009年提出了基于稀疏表示的二维人脸识别方法,该方法针对单幅正面姿态人脸图象进行识别。稀疏表示的识别方法基于一个简单的假设,即:同一类别的样本数据分布在更低维数的同一个子空间中,由此,将人脸识别问题看作通过稀疏描述对一系列线性回归人脸模型的分类问题。

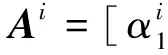
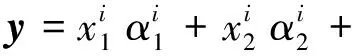
(1)

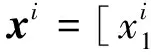
(2)

式中:A=[A1A2…Ai…AC]是一个包含C类子字典的结构字典,x=[0T0T…xiT… 0T]T是相应的稀疏描述向量。由于测试图像y的类别属性未知,因此假设它的描述x是对于整个训练集A,该描述能够通过稀疏描述过程来进行重建[7],公式如下:

(3)

或通过稀疏性约束公式:

(4)

式中：ε是重建误差参数,K是稀疏性级别level,描述了字典中的有效训练样本的个数。

由此,类别标记能够基于最小重建误差度量所获得,度量公式为:

(5)

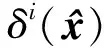
2 基于联合稀疏描述的多姿态三维人脸识别

本节重点介绍所提出的基于联合稀疏描述的多姿态三维人脸识别方法的具体步骤。识别系统框架如图1所示,首先,每一个个体通过不同视角采集得到多姿态三维人脸数据,组成多姿态测试人脸集,作为该识别系统的输入;其次,通过构建联合稀疏描述模型来对多姿态测试人脸集进行描述;最后,基于类别的重建误差,将有着最小重建误差的类别判定为测试数据所属的类别。

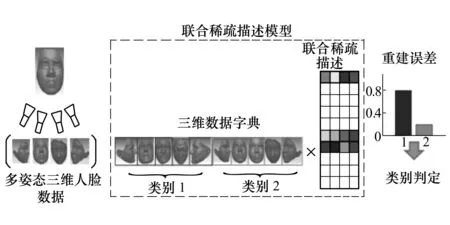
图1 多姿态三维人脸识别系统框架

2.1 三维空间联合字典

基于压缩感知理论,如果训练集足够大,能够包含全部必要的信息,那么任何一个训练集的样本都可以看作其他所有样本的线性组合[7]。在本文中,测试样本由一个超完备字典所描述,该字典的基本构成元素是全体训练样本及其一些基本的转换形式。由于三维数据的特殊结构形式,本文所构建的三维空间数据字典的方法具体描述如下:

1) 给定一个三维人脸数据,记为S,包含N个顶点,将全部顶点顺次排列描述三维人脸数据网格的拓扑连接结构,作为类字典的列向量。由于三维人脸数据的每一个顶点都包含3个参数,记为vi=(xi,yi,zi),因此列向量的每一个元素近似一个结构体,由3个分量组成,即:每一个列向量的维数为N×3。

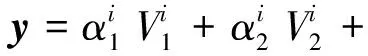
(6)

3) 整个训练集的超完备字典A可以由C个类别的共计S个训练样本的线性组合来构建,其表达式为:

(7)

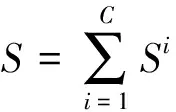
4) 由此,测试样本y可以由整体训练样本构成的数据字典来表示:

y=Aα0∈RN×3

(8)

式中,α0为稀疏系数。在本文中,由于字典的基本构成元素是三维数据,也就是说A的每一个元素描述了训练三维人脸数据中N个顶点的基本信息,而每一个顶点又由3个分量(xi,yi,zi)来描述,综合了3个分量的信息,因此所构建的超完备字典A分布在三维空间中,称之为三维空间联合字典。

对本文构建的三维超完备字典A,稀疏系数α0不是一个一维向量,而是一个三维矩阵,即:α0∈R3×S。由稀疏描述理论可知,α0是一个稀疏向量,理论上其元素值仅在与y相同类别所对应的位置上非零,其它位置上的值均为0。对于三维空间联合字典,重构出的稀疏向量α0的表达式为:

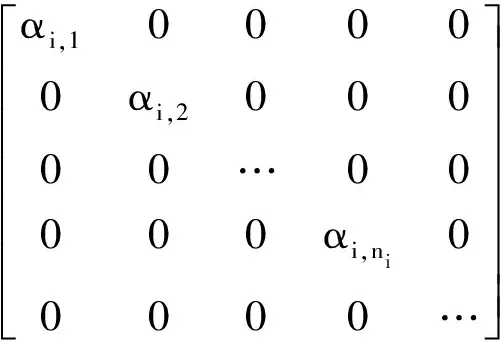
(9)

由三维空间联合字典A重构出的稀疏系数α0在三维空间上的分布情况如图2所示,可以看出,α0的非零系数分布在矩阵中心对角线附近。通过该三维稀疏向量α0,能够对测试数据y进行重建。

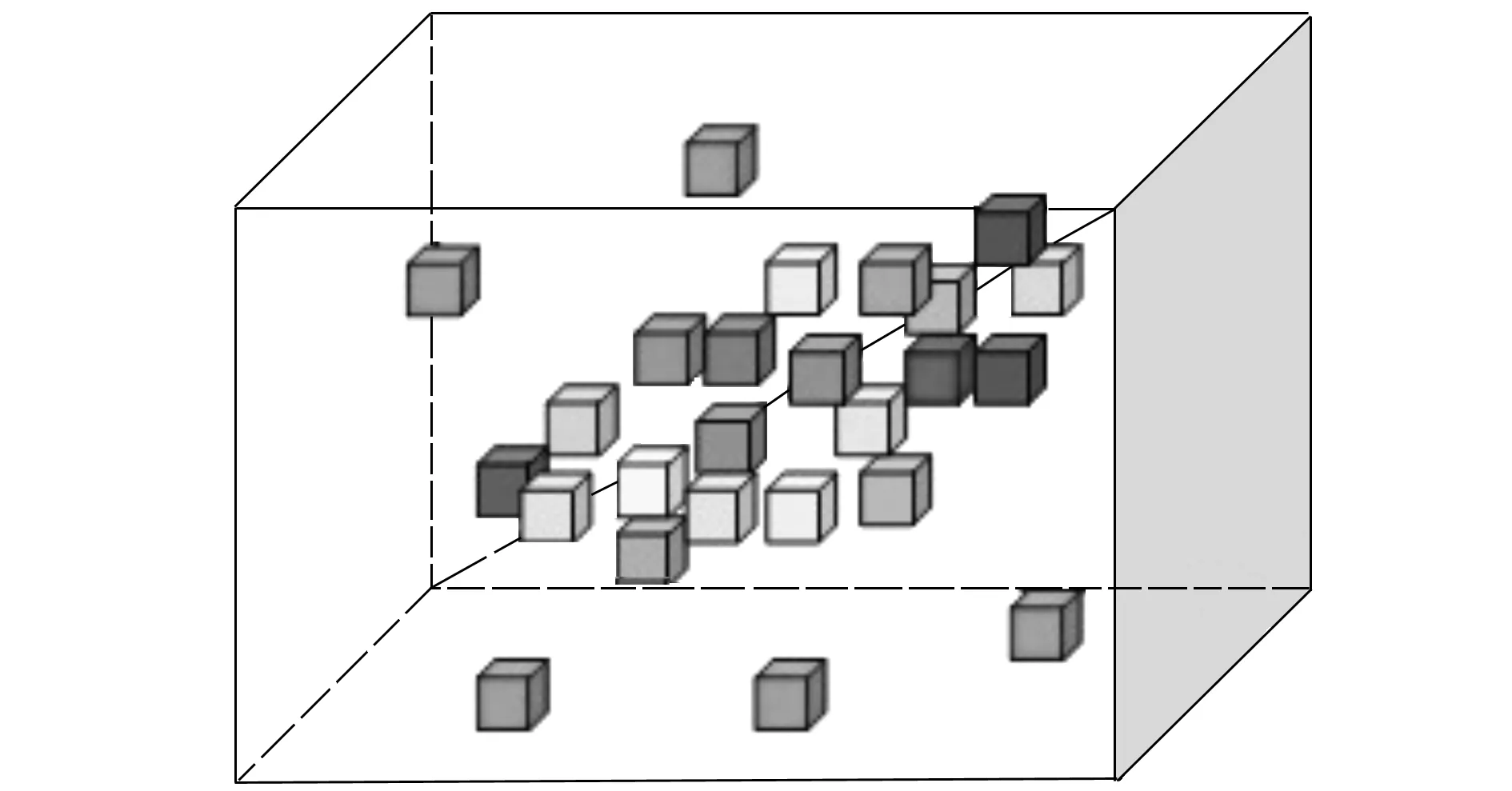
图2 三维稀疏系数分布示意图

2.2 联合稀疏描述模型

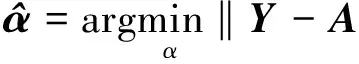
s.t. ‖α‖0≤K,

(10)

式中：K是稀疏性级别,描述了字典中有效数据元素的个数。

给定同一个体的M个不同视角观测数据,我们能够将M个稀疏描述问题(公式(10))合并为如下表达式:

s.t. ‖αi‖0≤K, ∀1≤i≤M

(11)

由于上式中求最小化步骤是在每一个视角内独立进行的,因此公式(11)并没有利用不同视角间的相互关系。而在多视角人脸数据识别应用中,由多视角得到的提示信息应该在联合稀疏描述中联合起来,用于增强联合稀疏重建的鲁棒性。为了联合获取到的所有视角图像的信息来进行识别,本文建立了一种联合稀疏性约束,来用于对向量的描述[12]。在该约束中,多维稀疏性描述向量有着同样的稀疏性类型,多视角观测样本的稀疏性描述能够通过对如下的最优化问题的联合求解重建得出:

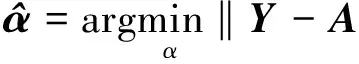
s.t. ‖α‖l0l2≤K

(12)

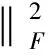
2.3 识别准则

(13)

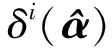
3 实验结果及分析

为了验证本文所提基于联合稀疏描述的多姿态三维人脸识别算法的有效性,采用国际公共三维人脸库FRGC2.0[13]进行对比实验,首先需要对人脸库中的数据进行预处理,包括去除杂点、补洞和平滑去噪等操作,得到质量较好仅包含人脸区域的三维数据。

3.1 实验数据集的选取

对FRGC2.0数据库通过仿真方法,构造多姿态变化子库。构造方法为:对每一个个体,选择一幅正面自然表情人脸数据,分别以x,y,z为对称轴,以15°为间隔单位在三维空间中进行旋转。按照以上方法,能够构造出多姿态三维人脸数据,并将其分为正面姿态(neutral frontal, NF),姿态变化较小(mild pose Variation, MPV)和姿态变化较大(wild pose variation, WPV)3个不同的子库,具体说明如表1所示。

表1 FRGC2.0姿态变化子库

3.2 观测集个数变化识别结果

将全部FRGC2.0多姿态变化数据作为训练集,构建三维空间联合超完备数据字典,分别将姿态变化子库NF、MPV、WPV、NF+MPV、NF+WPV作为观测集,构建多视角测试数据集,基于本文提出的联合稀疏描述识别方法JSRC来完成个体身份的识别,与相互子空间方法MSM[5]和稀疏表示识别方法SRC[7]进行对比,实验结果如表2和如图3所示。

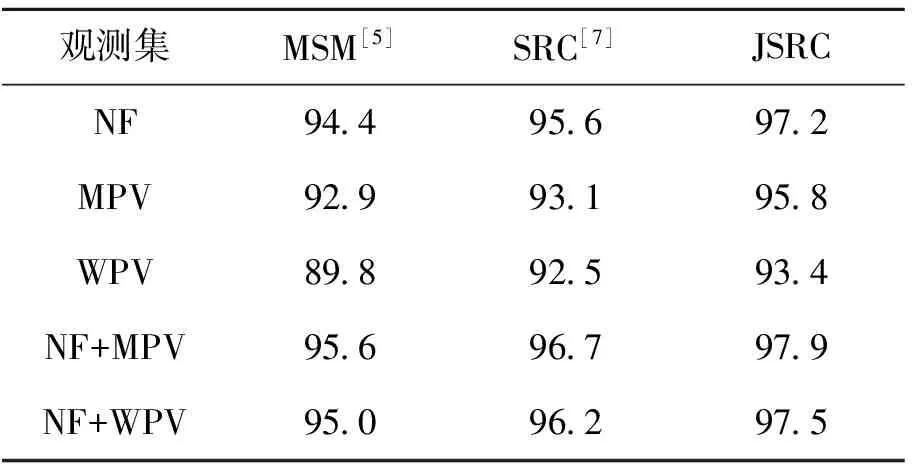
表2 不同观测集下的识别结果(%)

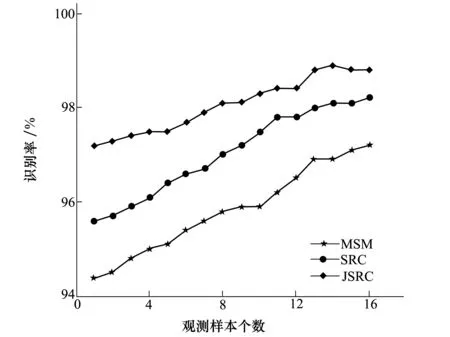
图3 观测集个数变化下的识别结果对比图

由实验结果可知,本文提出的JSRC方法在不同观测集下的识别率均高于MSM和SRC方法。表2中分别采用3个子集构建观测集,识别结果均出现了不同程度的降低,这是由于姿态变化后,人脸数据存在不同程度的缺失,因此在稀疏重构时会出现误差。而在采用NF与其他2个子集联合构建观测集后,识别率有了明显的提高,要高于单独采用单一子集时的识别率,说明多姿态联合识别的效果要高于单一姿态变化子集的效果。

由图3可以看出本文提出的JSRC方法对多姿态三维人脸的识别率要高于其他2种方法。值得注意的是,人脸识别率并非随着观测样本个数的增加,一直保持稳定增长态势,这是由于WPV子集中人脸的姿态变化较大,最高达到左、右90°的姿态变化。姿态变化过大时,同一个体的数据间差异大于不同个体间的数据差异,由此造成联合观测数据信息反而降低识别率的结果。

3.3 训练集个数变化识别结果

为了分析本文构建的联合稀疏描述模型中三维空间联合字典的大小对识别结果的影响,本小节通过改变训练集的个数,构建不同维数的三维空间联合字典,对同一组观测样本进行识别,检测联合稀疏描述模型对训练数据个数的鲁棒性。训练集个数的选取原则为,对于3组姿态变化子集,分别构建NF+3个MPV数据、NF+MPV、NF+MPV+3个WPV数据、NF+MPV+6个WPV数据、NF+MPV+WPV共5组训练集,建立联合稀疏描述模型,用于对测试数据进行识别。该小节中,测试数据集选取1个正面姿态数据,1个MPV中姿态变化较小数据和1个WPV中姿态变化较大数据。与MSM和SRC方法的对比结果如表3所示。

表3 训练集个数变化下的识别结果对比表(%)

由表3可以看出,本文提出的JSRC方法对不同训练集下的识别结果均高于其他2种方法。随着训练集个数和包含姿态变化多样性的增加,对同一测试集的识别结果稳步提高。这一结果说明训练集个数的增加,由训练集构建的三维空间联合字典所包含的信息量也随之增加,由此稀疏重构出的系数矩阵和重建结果也更加准确。

4 结 论

针对多姿态三维人脸的识别问题,本文提出了基于联合稀疏描述的识别方法(JSRC),构建三维空间联合字典,并进一步构造联合稀疏描述模型,利用多幅视图组成测试集完成人脸分类。JSRC方法能够利用所有视图的相互关系,避免单独对待每一个观测值时所潜在的错误判别风险,大大提高识别准确率。在国际公开三维人脸数据库FRGC2.0的对比实验表明了本文方法在多姿态三维人脸识别的有效性。

参考文献：

[1] Bowyer K W, Chang K, Flynn P. A Survey of Approaches and Challenges in 3D and Multi-Modal 3D+2D Face Recognition[J]. Computer Vision and Image Understanding, 2006, 101(1):1-15

[2] Farhat M, Alfalou A, Hamam H, Brosseau C. Double Fusion Filtering Based Multi-View Face Recognition[J]. Optics Communications, 2009, 282 (11): 2136-2142

[3] Kokiopoulou E, Frossard P. Graph-Based Classification of Multiple Observation Sets[J]. Pattern Recognition, 2010, 43 (12): 3988-3997

[4] Cevikalp H, Triggs B. Face Recognition Based on Image Sets[C]∥Proceedings of Computer Vision Pattern Recognition, 2010, 2567-2573

[5] Fukui K, Yamaguchi O. Face Recognition Using Multi-Viewpoint Patterns for Robot Vision[J]. Springer Tracts in Advanced Robotics, 2005, 15: 192-201

[6] Hamm J, Lee D D. Grassmann Discriminant Analysis: A Unifying View on Subspace-Based Learning[C]∥Proceedings of ICML, 2008, 376-383

[7] Wright J, Yang A Y, Ganesh A, et al. Robust Face Recognition via Sparse Representation[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227

[8] Li X, Jia T, Zhang H. Expression Insensitive 3D Face Recognition Using Sparse Representation[C]∥Proceedings of Computer Vision Pattern Recognition, 2009: 2575-2582

[9] Guo Z, Zhang Y, Xia Y, et al. Multi-Pose 3D Face Recognition Based on 2D Sparse Representation[J]. Journal of Visual Communication and Image Representation, 2013, 24(2): 117-126

[10] Tang H, Sun Y, Yin B, et al. 3D Face Recognition Based on Sparse Representation[J]. The Journal of Supercomputing, 2011, 58(1):84-95

[11] Rakotomamonjy A. Surveying and Comparing Simultaneous Sparse Approximation (or Group Lasso) Algorithms[R]. Technical Report, 2010

[12] Tropp J A, Gilbert A C, Strauss M J. Algorithms for Simultaneous Sparse Approximation[J]. Eurasip Journal on Applied Signal Processing, 2006, 86: 572-588

[13] Phillips P, Flynn P, Scruggs T, et al. Overview of the Face Recognition Grand Challenge[C]∥Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition, 2005, 947-954