PMSM 最优自适应CDKF 估计方法

丁国强，徐 洁，熊 明，乔相伟

(1．郑州轻工业学院 电气信息工程学院，河南 郑州450002;2． 郑州轻工业学院 软件学院，河南 郑州450002;3．西安航天精密机电研究所，陕西 西安710100)

0 引言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)控制系统利用传感器感测转子转速、角位移实现闭环控制，易于实现，但当电机环境温度变化和磁饱和等电机参数发生变化使调速性能下降，鲁棒性较差［1］，限制PMSM 系统应用，因此无传感器控制参数估计转子转速和位置参数成为目前PMSM 系统研究热点． PMSM 电机无传感控制法主要有开环计算法［2］、高频注入法［3］等非理想特性算法和电机参数观测器模型闭环控制算法．而利用PMSM 参数观测器递推估计转速、位置角位移方法具有动态稳定性能好等优点［4］，目前常用估计算法有Kalman 法、EKF法、UKF 法以及插值滤波算法(DDF)等，将受控系统模型和递推估计算法结合得到协方差矩阵满足电机控制要求，中心差分滤波(CDKF)算法精度和计算稳定性优于UKF 算法［5］，适用于PMSM系统参数估计快速性和高精度稳定计算． 笔者针对非线性系统噪声未知情形，提出利用新息和残差在线自适应估计其特性的自适应CDKF(ACDKF)算法，来同时获得过程噪声和观测噪声的统计时变特性，改善系统最优估计性能．

笔者采用两相静止坐标αβ 轴系建立PMSY数学模型，采用ACDKF 算法开展电机转速和角位移实时估计．仿真结果表明:系统ACDKF 参数估计算法优越性和良好抗干扰性能，转速和角位移估计精度高，数值计算稳定．

1 非线性永磁同步电机模型

在静止αβ 轴坐标系中推导永磁同步电机定子电流方程［6］

式中:Iα、Iβ和Uα、Uβ分别代表定子电流和电压轴向分量;ωr、θr表示转子角速度和转子角位移;P、Rs、Ls和ψf分别表示极对数、定子电阻、定子电感和转子永磁体磁链．

在αβ 轴系中PMSM 状态方程取定子电流轴向分量、电机转速和角位移作为系统状态变量，则转子角位移微分方程为

PMSM 中存在负载阻力变化和摩擦力扰动量以及齿槽和边端效应产生的磁阻力引起推力变化以及转子和定子谐波磁场相互作用产生的推力变化等不确定物理因素［7-8］都看作不确定扰动分量随机噪声处理．转速变化过程时间常数一般都远大于电磁时间常数，估算周期中转速视为常数［9］，则有转子转速微分方程为

这种偏差假设在ACDKF 算法中作为系统状态噪声处理，由算法递推计算校正．电流传感器检测PMSM 三相电流，经由abc 系转化到αβ 轴系中获得两相输出电流Iα、Iβ，把Iα、Iβ作为系统观测量，其中观测噪声以Gauss 白噪声对待，则系统观测方程

Z=Hx+v． (4)

其中H=［I2×20 0］，I2×2表示单位阵．

2 CDKF 估计算法

考虑式(1)～(3)组成的PMSM 非线性系统函数，式(4)作为观测方程组成PMSM 系统离散状态空间模型

协方差矩阵为

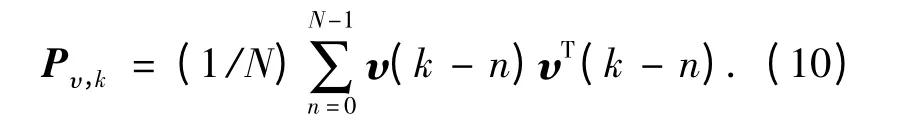
式中:N 表示平滑估计窗口大小．

观测噪声协方差R 实时估计值可计算为

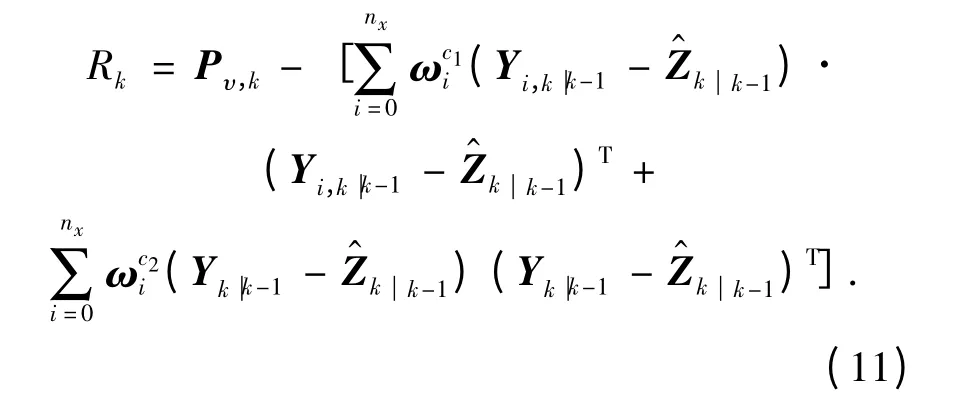
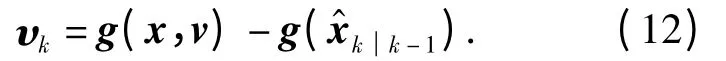
对其实施二阶Stirling 插值逼近计算可得到

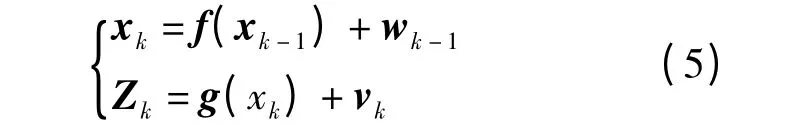
式中:x =［Iα，Iβ，θr，ωr］T是PMSM 系统状态向量;Z=［Iα，Iβ］，过程噪声wk-1和两相观测电流噪声vk相互独立，有wk-1～N(0，Qk-1)，vk～N(0，Rk)统计特性．CDKF 算法详细计算过程可参阅文献［5］．

3 CDKF 估计中噪声自适应估计算法

最优估计中观测向量序列与k 时刻参数向量估计值经由观测方程计算得到观测量估计值之差定义为残差［9］

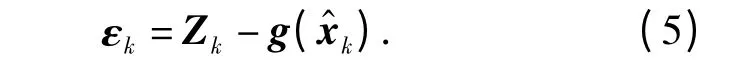
那么状态向量与其一步预测值差值为状态预测误差

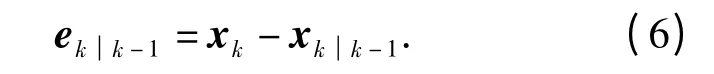
状态向量与其k 时刻估计值差值为状态估计误差

由观测向量与其一步预测值之差定义新息

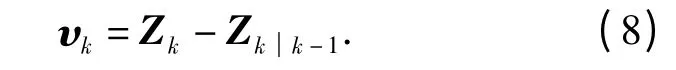
观测向量预测误差方差矩阵为

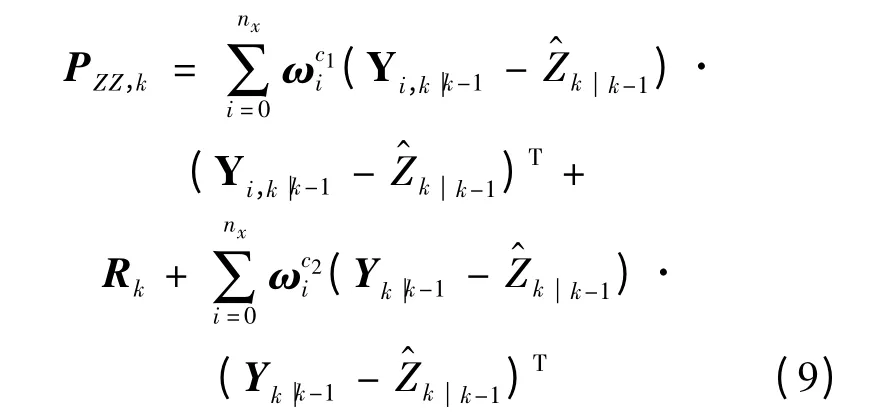
那么利用开窗法平滑［9］计算新息实时估计误差

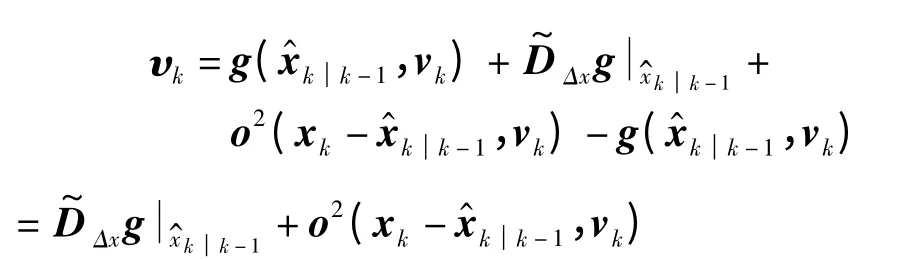
并对其整理后获得

很明显Stirling 插值多项式的二阶及其高阶项带来高阶截断误差，引入自适应因子对角阵

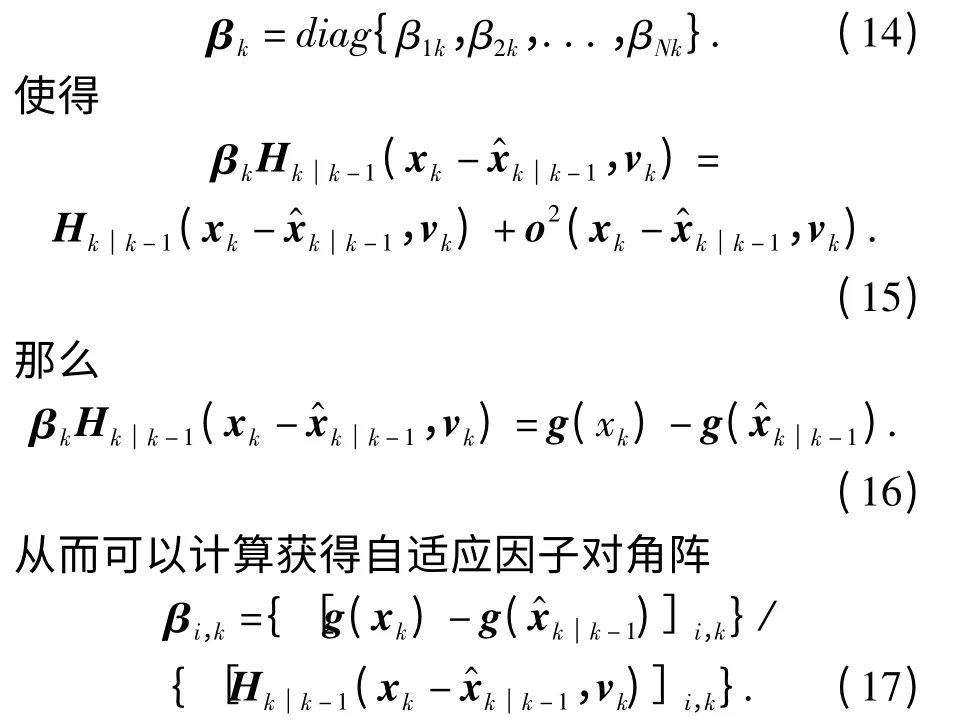
式中:i，k 下标表示N ×1 矩阵的第i 行元素;βi，k表示对角阵的第i 个元素，新息表达式可以进一步整理为类似地估计残差也按照这个思路可表示为

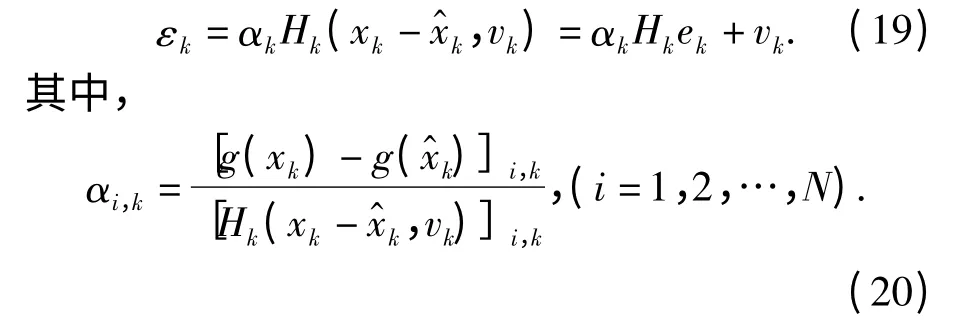
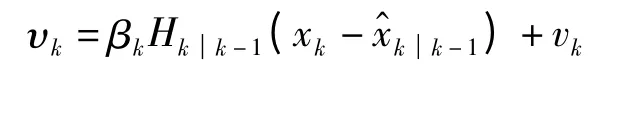
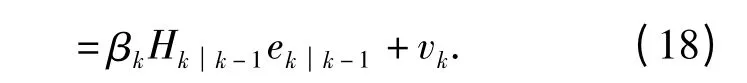
为了使残差与新息表达式系数一致，引入自适应对角阵γk，使得

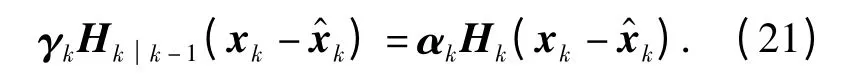
成立．则估计残差可进一步整理为

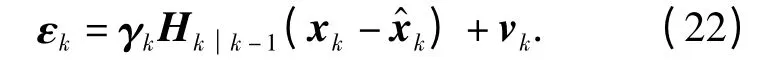
那么利用新息与残差正交原理可得到

同时把CDKF 算法中状态向量一步预测协方差矩阵计算式代入上式中获得过程噪声协方差Qk-1在线估计计算表达式

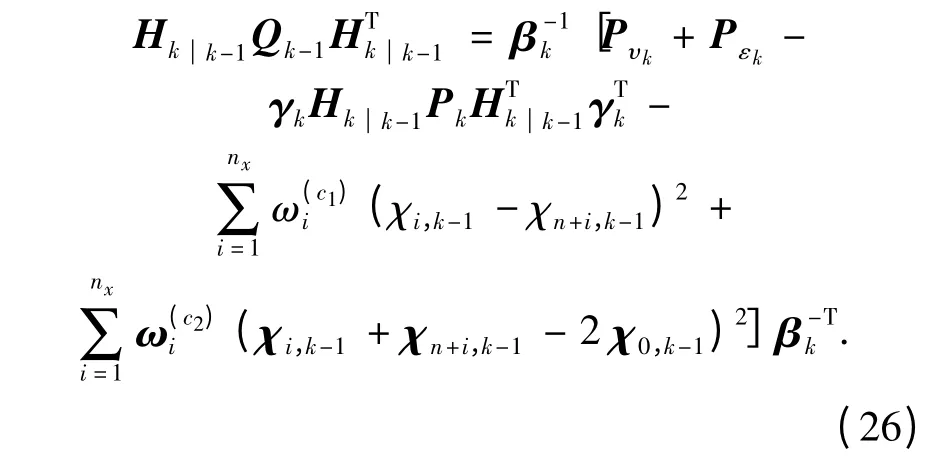
那么利用式(25)和式(11)分别对过程噪声和观测噪声实施在线实时估计计算，结合CDKF 算法预测更新迭代操作，实现自适应CDKF 算法．

4 ACDKF 算法实验仿真研究

4．1 无传感器PMSM 驱动系统

无位置传感器PMSM 驱动系统结构如图1 所示，系统利用零直轴电流最大推力控制策略实现转速和电流双闭环控制系统结构，转速控制器采用PI 控制算法，输出交轴电流I*q 信号作为参考，电流控制器采用两个相同参数的PI 控制器分别控制直轴和交轴电流，其输出作为驱动逆变器的SPWM 信号，利用估计器观测转子转速及转子角位移，永磁同步电机的参数设置如表1 所示．

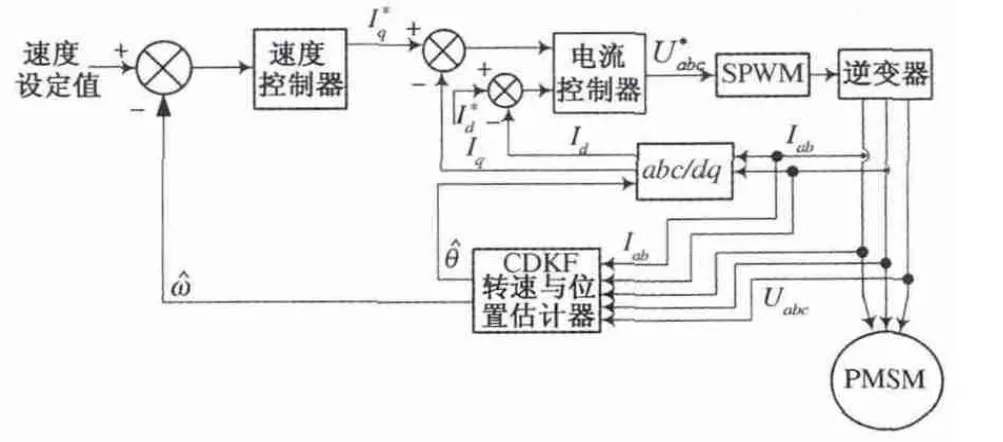
图1 PMSM 电机驱动系统结构图Fig．1 PMSM Motor drive system structure

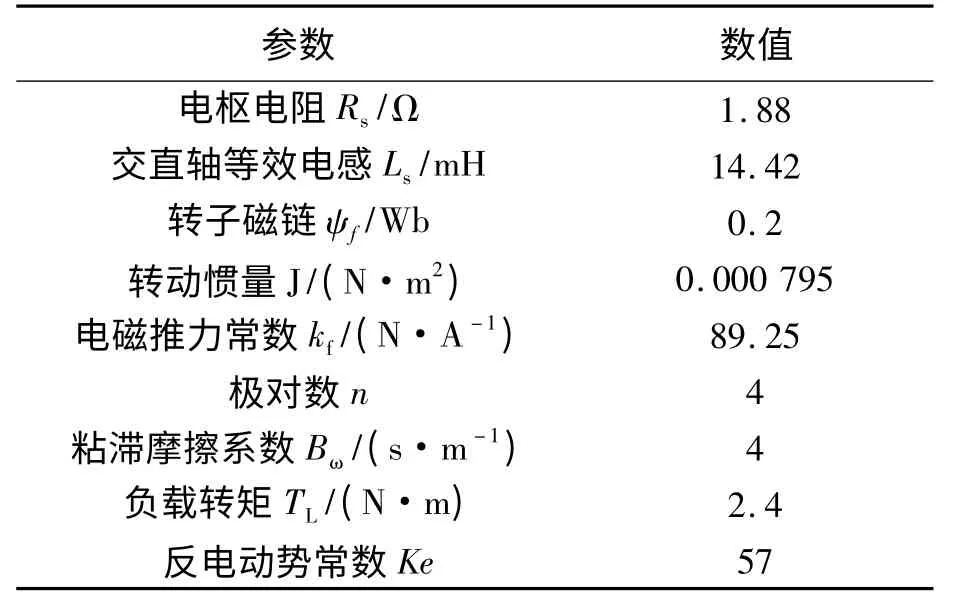
表1 PMSM 主要参数Tab．1 PMSM main parameter

4．2 实验仿真分析

为了验证ACDKF 算法计算性能，笔者采用ACDKF 和CDKF 算法对PMSM 驱动系统进行对比试验仿真研究． PMSM 驱动控制系统中转速控制环控制速度，不需要角位移，在最优估计算法参数优化基础上以转速估计性能最优确定辨识算法的参数优化数值． 最优估计算法初始化数值设置如下:设定PMSM 驱动系统电机启动磁极角位移为60°，也就是系统初始位置误差5．33 mm，转子转速和电流均设为0，系统误差方差矩阵初值设置为

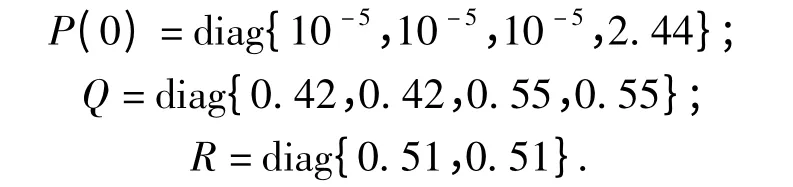
利用两种估计算法输出信息作为磁极角位移及转子速度反馈值来获得PMSM 驱动系统的转子转速仿真数据如图2 的CDKF 算法速度估计和图3 的ACDKF 算法速度估计数据所示．

对比看出ACDKF 算法估计性能明显优于CDKF 算法，ACDKF 算法速度估计误差仅在初始0．5 s 内存在，在此之后估计误差能够稳定在0 轴上，在估计时间内ACDKF 算法速度估计误差仅有0．006 3 rad/s，而CDKF 算法由于无法处理噪声时变统计特性，估计误差曲线始终都存在偏差，可以看到在起始的0．3 s 之内电机转子转速估计误差在启动时比较大，可达到±3 rad/s 的误差，但在随后时间内在±1 rad/s 范围之内波动，速度估计方差均值为0．4，速度估计均值误差达到0．217 rad/s．

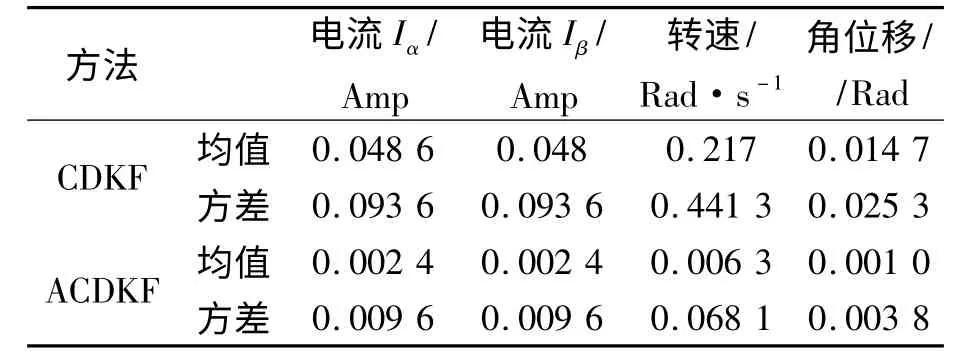
表2 PMSM 参数估计误差数据表Tab．2 PMSM parameter estimation error data table

这说明ACDKF 算法能够有效改善PMSM 系统状态参数数值计算稳定性，ACDKF 算法能够有效抑制滤波发散，加快收敛速度，计算精度得到明显提高，显示出自适应算法更加灵活可靠的计算优势．

图2 电机转子转速仿真数据(CDKF 算法)Fig．2 PMSM rotor speed simulation data (CDKF)

仿真中定子电流加入了Gauss 白噪声，从获得图4 和图5 转子角位移仿真比较数据和误差数据曲线可知CDKF 和ACDKF 估计器都能够快速准确估计出PMSM 电机转速和转子角位移，CDKF算法在起始0．5 s 时间内转子位置估计较大，但在随后时间稳态运行中估计方差为0．025 3．同时也应该看到两种最优估计算法中转子转速估计值稍微滞后于电机转速实际值，原因在于估计器建模时假设采样时间内速度导数为0，在原理上形成了这种误差．PMSM 电机带载12 N·m，估计算法计算估计速度信号实现速度环反馈，起动过程中转子角速度估计值跟踪误差比较大，经过多步递推计算后估计角速度和实际角速度基本上能够实现无偏差跟踪，从而验证了2 种估计算法实现无传感PMSM 控制系统状态参数估计有效性．

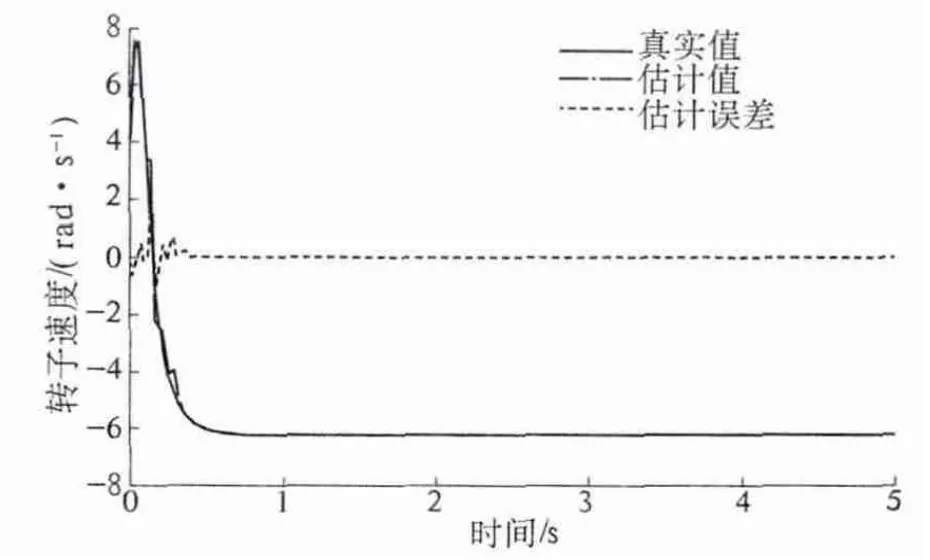
图3 电机转子转速仿真数据(ACDKF)Fig．3 PMSM motor rotor speed simulation data (ACDKF)

但是从图4 和图5 中电机转子角位移估计误差可以看出，ACDKF 算法具有较快的收敛速度，仅在初始0．4 s 内估计值与实际值之间存在偏差，但随后很快就能稳定在0 轴上面，说明ACDKF 算法对系统噪声具有较强的修正作用，而CDKF 算法的估计误差始终都在一个较小范围内波动．

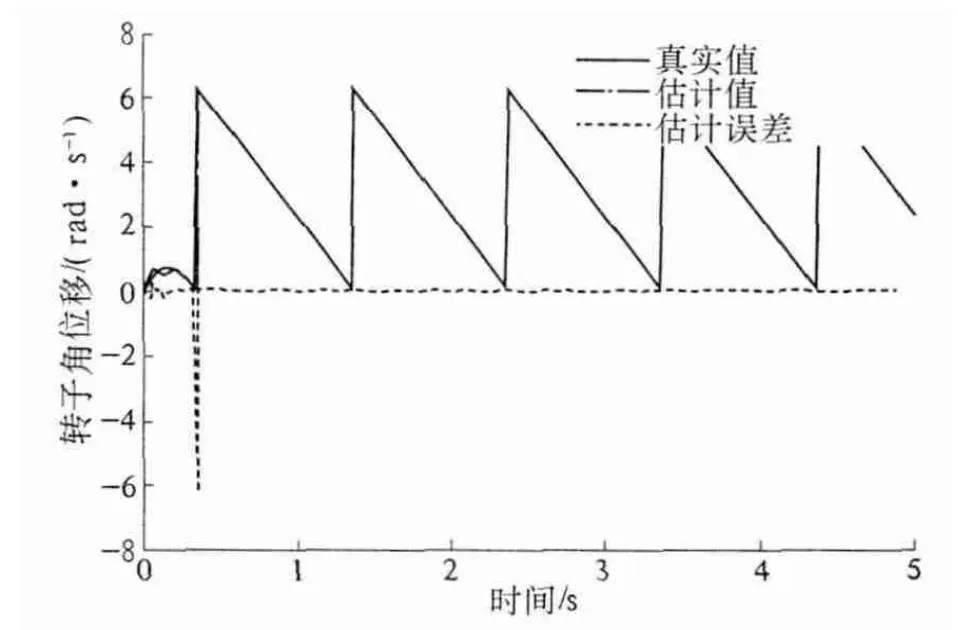
图4 电机转子角位移仿真数据(CDKF 算法)Fig．4 PMSM motor rotor angular displacement simulation data (CDKF)

5 结论

针对无传感PMSM 双闭环系统快速稳定控制要求，基于CDKF 算法设计系统噪声自适应调整算法构建ACDKF 估计算法，对PMSM 非线性状态空间模型以及线性观测方程，利用CDKF 和ACDKF 最优估计算法展开PMSM 状态参数最优估计对比仿真研究． 仿真结果表明两种估计算法都能够获得PMSM 转速和角位移估计，估计误差较小，相比之下ACDKF 算法收敛速度较快，数值计算稳定性较好，能够获得PMSM 转子转速和角位移精确估计．

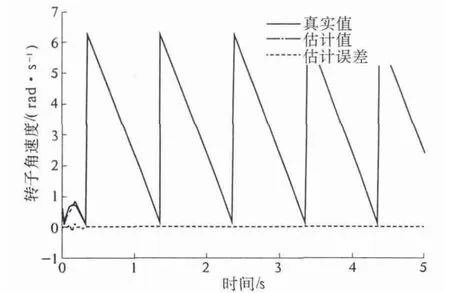
图5 电机转子角位移仿真数据(ACDKF 算法)Fig．5 PMSM Motor rotor angular displacement simulation data (ACDKF)

［1］ 李铁才，杜坤梅.电机控制技术［M］． 哈尔滨:哈尔滨工业大学出版社，2000．

［2］ 鲁文其，胡育文，梁骄雁，等． 永磁同步电机伺服系统抗扰动自适应控制［J］． 中国电机工程学报，2011，31(3):75 -81．

［3］ 张宇辉，陈峰，李惠敏，等． 基于小波变换和矩阵束算法的同步电机参数辨识［J］． 电力系统保护与控制，2012，40(9):87 -92．

［4］ 曹明凯，韩超先，马平，等．利用励磁电压扰动后的同步发电机参数辨识［J］． 电力系统保护与控制，2012，40(19):116 -120．

［5］ 丁国强，崔光照，周卫东，等． 传递对准MRP-CDKF 算法［J］． 华中科技大学学报:自然科学版，2011，41(1):127 -132．

［6］ 皇甫宜耿，刘卫国，马瑞卿． 非线性永磁同步电机建模方法与仿真［J］． 电气传动自动化，2008，30(6):30 -33．

［7］ 孙旭霞，刘博． 基于EKF 的PMSM 无传感器控制及滤波参数选取［J］．微特电机，2011，39(5):39-46．

［8］ 王磊，李颖晖，朱喜华，等．存在扰动的永磁同步电机混沌运动模糊自适应同步［J］． 电力系统保护与控制，2011，39(11):33 -37．

［9］ SALAHSHOOR K，MOSALLAEI M，BAYAT M． Centralized and decentralized process and sensor fault monitoring using data fusion based on adaptive extended Kalman filter algorithm［J］． Measurement，2008，41(10):1059 - 1076．

［10］杨元喜，徐天河．基于移动开窗法协方差估计和方差分量估计的自适应滤波［J］．武汉大学学报:信息科学版，2003，28(6):714 -718．

［11］于洪霞，胡静涛． 基于EKF 的异步电机转速和负载转矩估计［J］． 仪器仪表学报，2011，32(2):329-335．