统计方法在确定黄土湿陷起始压力中的应用

焦振华, 李　鹏

(陕西省水利电力勘测设计研究院,陕西 西安　710001)

0　引言

中国的黄土面积>44×104km2,约占国土面积的4.6%。黄土多为非饱和土,具湿陷性,即一定压力作用下,受水浸湿后,结构迅速破坏,发生显著湿陷变形,同时强度随之降低,常使构筑物发生破坏,严重影响建筑物的使用[1]。中国学者对黄土的沉积环境、物理力学特性、湿陷的机理及湿陷与物理力学参数的关系进行了大量的理论研究[2-4],认为黄土湿陷为多因素综合控制的结果。水与压力为黄土湿陷的主要外在影响因素,孔隙、密度对黄土湿陷也具有很大影响。同时,统计与技术分析上,聚类分析、因子分析、模糊判别及其他数理统计方法也愈来愈多的应用于黄土湿陷性研究当中[5-7],统计分析中充分考虑了影响因子之间的相关性,消除了多重共线性的影响,将天然重度、重度、孔隙比对湿陷影响归为一类,而将含水率和塑性指数分别归为一类,并用归类后指数进行线性拟合计算湿陷量分析湿陷等级,结论与实际完全吻合。对黄土地层进行勘察评价,特别是黄土渠道工程评价中,黄土湿陷起始压力指标必不可少[8],有关学者对黄土湿陷起始压力的应用做了一定研究[9]认为该指标对控制填方最大限度、确定挖方后的地基湿陷类型、地基处理厚度、承载力特征值等有较大的作用。求黄土湿陷起始压力的方法室内宜用双线法,野外宜用饱水荷载法。采用湿陷起始压力值作为地基承载力时,不会危及建筑物的变形,也不会发生湿陷。

综上所述,前人主要对黄土的湿陷性、湿陷等级及其影响因素进行了相关探讨,而对湿陷起始压力这一重要指标仅从其工程重要性及试验过程中应注意的主要问题进行了阐述和总结。本文为探讨黄土湿陷起始压力的影响因素,进一步通过各影响因素计算黄土湿陷起始压力,与试验起始压力进行对比分析,以期更准确地确定起始压力的数值,验证试验结果,并将该指标更好地应用于工程实践。

1　统计分析理论及思路

研究表明,黄土物理性质中对湿陷影响的变量不是相互独立,而是相互联系的。其对湿陷性影响的贡献大小不一。其相关性和贡献差异性导致了随机变量的多重共线性。

因子分析是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系,探求观测数据中的基本结构,并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。而聚类分析是一组将研究对象分为相对同质群组的统计分析技术。因子分析与聚类分析可以以最少的信息丢失,将原始的因子变量综合成较少的互相独立的因子变量,使用这些因子分析后的综合变量代替原始变量参与回归模型,既可不丢失原始变量的信息,又可消除多重共线性。

本文拟先对各物理性质进行聚类分析,将原始因子变量综合成较少的相互独立的代表性变量,之后对综合变量进行线性回归,探讨统计方法计算黄土湿陷起始压力的可行性。

2　模型建立及统计

本文拟对陕西省彬县一带37组黄土实测数据中物理性质变量进行统计分析(含水率、天然密度、孔隙比、液限、塑限等5项指标),以期通过该变量统计确定黄土湿陷起始压力(表1)。

表1　黄土的实测数据

设x1、x2、x3、x4、x5分别表示含水率、天然密度、孔隙比、液限、塑限,y表示湿陷起始压力进行统计。

2.1　相关性分析

通过对各参数与黄土湿陷起始压力及各参数相互间进行相关性分析(图1、图2)。

由图1可见,各参数与黄土湿陷起始压力之间,天然密度相关性最大,R2=0.305 6(相关系数为0.55),中度相关;含水率、孔隙比及液限低度相关,R2分别为0.2151,0.157,0.119 7,相关系数为0.3～0.5;塑限不具相关性,R2为0.0746,相关系数<0.3。

由图2可见,在与黄土湿陷起始压力相关的各参数之间,天然密度与孔隙比高度相关,R2=0.856 7(相关系数为-0.92),天然密度与含水率,含水率与液限低度相关,R2分别为0.156 7,0.144 7,相关系数为0.3～0.5。存在一定的信息重叠。为消除该信息重叠,本文对上述与黄土湿陷起始压力相关的指标进行因子分析。

图1　各指标与湿陷起始压力相关性

2.2　因子聚类分析

利用相关分析得到的因子间相关系数建立矩阵进行聚类分析,将相近因子归为一类。具体做法是选取贴近度α(为描述因子间相近程度的比例系数,本文取0.8)将矩阵中小于α的元素记为0,大于α的元素记为1。因子相关系数矩阵见式(1),聚类后矩阵见式(2)。

(1)

(2)

由式(2)可知,将天然密度、孔隙比聚为一类,含水率、液限各为一类,即{x1},{x2,x3}, {x4}。

2.3　因子主成分分析

使用SPSS软件对聚合类{x2,x3}进行因子主成分分析,提取到一个主成分F,其总方差解释见表2。

由表2得出,所提取的主成分F对原变量x2、x3的解释程度达95%以上,可以选择所求得的综合因子进入后续分析过程。

图2　各指标间相关性

表2总方差解释

Table 2The explanation of total variance

元素初始特征值提取出的平方和总和值方差/%累积值/%总和值方差/%累积值/%11．92696．27896．2781．92696．27896．27820．0743．722100．000

获取总方差后得到主成分F的因子得分系数见表3。

表3　因子得分系数

由表3可得出因子得分函数为：

F=0.981(x2-x3)

(3)

2.4　结论检验

将主成分F、变量x1、x4与湿陷起始压力y一起进行线性回归,得到线性回归方程为:

y=-584.96+8.64x1+178.09F+11.127x4

(4)

将主成分还原为原始变量后回归方程为:

y=-584.96+8.64x1+174.71(x2-x3)+11.127x4

(5)

依上式求得湿陷起始压力试验湿陷起始压力做相关分析(图3),相关系数可达0.65(R2=0.4173),较各单因素与试验起始压力相关性大大提高,进一步说明湿陷起始压力为多因素共同影响的结果,在实践过程中应综合各参数校对分析湿陷起始压力试验结果。

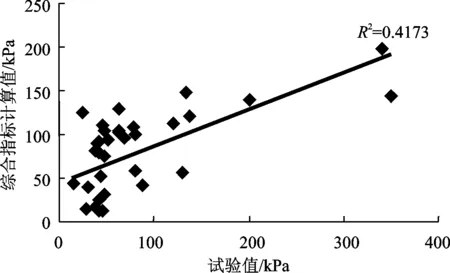
图3　黄土湿陷起始压力综合指标计算值与试验值相关性

3　结语

黄土地区尤其是管线工程,黄土湿陷起始压力指标的确定有重要的工程意义,本文基于因子分析,主成分分析及线性拟合等统计方法,研究了黄土样品的5个物理性质,得出以下结论:

(1)天然密度与黄土湿陷起始压力相关性最大,为中度相关;含水率、孔隙比及液限低度相关;塑限不具相关性。

(2)在与黄土湿陷起始压力相关的各参数之间,天然密度与孔隙比高度相关,天然密度与含水率,含水率与液限低度相关,存在一定的信息重叠。

(3)湿陷起始压力为多因素综合作用结果,对各物理力学参数的综合统计可在确定黄土湿陷起始压力过程中提供一定参考。

参考文献：

[1]张炜,张苏民.我国黄土工程性质研究的发展[J].岩土工程学报,1995,17(6):80-88.

[2]庞旭卿,倪万魁.黄土的湿陷特性研究及湿陷等级评判[J].工程地质学报,2006,14(增刊):151-156.

[3]高国瑞.黄土湿陷变形的结构理论[J].岩土工程学报,1990,12(4):1-10.

[4]高凌霞.黄土湿陷系数与物理指标间的定量关系[J].大连民族大学学报,2004,6(5):63-65.

[5]任新玲.影响黄土湿陷系数的数理统计分析[J].山西交通科技,1995(5):19-21.

[6]陈开圣,彭小平.模糊综合评判法在黄土湿陷性评价中的应用[J].公路交通科技,2005,22(9):16-19.

[7]徐志军,郑俊杰,张军,等.聚类分析和因子分析在黄土湿陷性评价中的应用[J].岩土力学,2010,31(增刊):407-411.

[8]濮声荣.工程地质实践与探索[M].西安:陕西科学技术出版社，2012.

[9]关文章.论湿陷起始压力[J].工程地质学报,1993(创刊号):85-92.