粗糙条件熵算法在故障诊断中应用分析
皮安云,于 鹏,王文双,张光轶
(1.91868部队,海南三亚572106;2.海军装备部军械保障部,北京100036;3.海军航空工程学院科研部,山东烟台264001)
粗糙集在故障诊断中可以有效消除冗余和不精确的故障信息,且不需要任何先验信息。目前,在粗糙集中较经典的约简算法有:属性重要度算法、差别矩阵算法、差别函数算法和条件熵算法等[1-4]。其中,条件熵算法可以克服单纯差别矩阵算法对属性重要性约简过于简单且忽视条件属性实际意义的缺点,同时又能弥补分类质量视角下,属性重要性忽视条件属性间内在联系的不足。本文将条件熵算法应用到弹载数传电台设备的故障诊断中,结果表明故障诊断不仅准确有效,而且简单快速。
1 粗糙集及条件熵算法
1.1 粗糙集及条件熵
在粗糙集理论中,四元组S=(U,A,V,f)是一个知识表达系统(信息系统)。其中,U为论域;A为属性集;是属性α的值域;f:U×A→V是一个信息函数,它为每个对象的每个属性赋予一个信息值,即∀α∈A,x∈U,f(x,α)∈Vα。
若A=C⋃D,C⋂D=∅,C为条件属性值,D为决策属性值,则知识表达系统S称为决策表[5-6]。
在决策表中,需要考虑的是哪个条件属性对决策更重要,这就需要考虑条件属性与决策属性之间的互信息或者条件熵[7-8]。这里,假设决策属性D在论域U上的划分为D:D={D1,D2,…,Dm},则定义条件属性C相对于决策属性D的一个条件信息熵为:
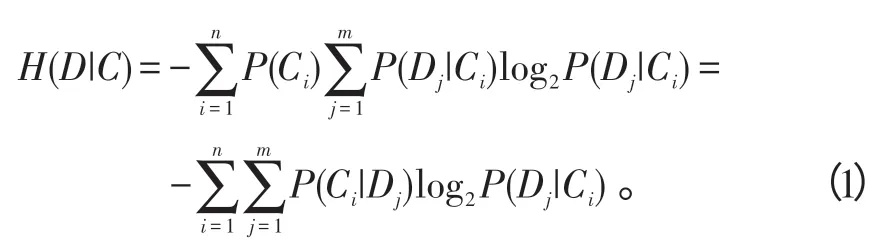
式(1)中:P(Ci) 为条件属性Ci的概率;P(Dj|Ci) 和P(Ci|Dj)分别为条件概率。
由条件熵的定义可知,若条件属性Ci完全属于决策属性Dj,则P(Dj|Ci)=1,log2P(Dj|Ci)=0 。若所有log2P(Dj|Ci)=0,则H(D|C)=0,即为一致性决策系统[9]。可见,条件信息熵衡量了决策系统的整体不确定性。
由定义可知,如果决策表条件属性集的分类进行合并,将可能导致条件熵上升,只有在发生合并的两个分类对于决策类的隶属度(概率)相等的情况下,才不导致条件熵的变化[10-12]。
1.2 条件熵约简算法
条件信息熵的约简算法步骤归纳为:
Input:决策表S=(U,A,V,f),A=C⋃D;
Output:决策表的一个最小约简REDC(D)。
①计算决策表S中决策属性集D相对条件属性C的条件信息熵H(D|C);②计算条件属性C相对决策属性D的核CORED(C),令Att=C-CORED(C);③令RED=CORED(C),对αi∈Att,计算H(D|RED ⋃{αi});④选择使H(D|RED ⋃{αi})最小的属性αj,若同时有多个属性达到最小值,则从中选一个在差别矩阵中出现最多的属性。令Att=Att-{αj},RED=RED ⋃{αj},计算H(D|RED),若H(D|RED)=H(D|C)则终止,否则转③。
1.3 复杂度分析
在最坏情况下,每次所考虑的属性数依次为n,n-1,…,1(n为决策表的条件属性数)。故总次数为n+(n-l)+…+l=n(n+l)/2。如果忽略对象数对计算时间的影响,那么,在最坏情况下,该算法能够在o(n2)时间复杂性内找到满意约简。与经典基于差别矩阵的约简算法的复杂度为o(Ln2)(L为CORED(C)中元素个数)[13]的时间复杂性相比,该算法较优。
2 弹载数传电台设备中故障诊断应用
本文以某弹载数传电台设备为诊断对象,故障诊断定位到模块级。整个电台由坐标模块1、频综模块2、接收机模块3、微机模块4、解调模块5、同步模块6、功放模块7、激励模块8 和接口模块构成。每种故障现象的发生都是由于某个甚至某几个模块出现故障而导致,模块出现故障其征兆表现为相关性能指标超出标称值范围,即所谓的测试超差。
针对设备的特征,选取了最典型4种异常情况:数传电台不受控制,常规收发都异常,抗干扰收发都异常和坐标数据异常。将9个模块可能发生的故障定义为“1”,正常定义为“0”,并从该设备故障数据库中选择故障样本,对这些样本数据预处理:①进行条件属性的简化。即从原始决策表中消去在所选的故障中没有变化的列,本例中即消去3 种故障类型中都会故障的“接口模块”;②消去重复行。因为重复行表示重复的故障样本,即同样的决策,所以可以消去,从而得到原始决策表,见表1。表1 中:0 代表正常,1 代表数传电台不受控制,2 代表常规收发都异常,3 代表抗干扰收发都异常,4代表坐标数据异常。
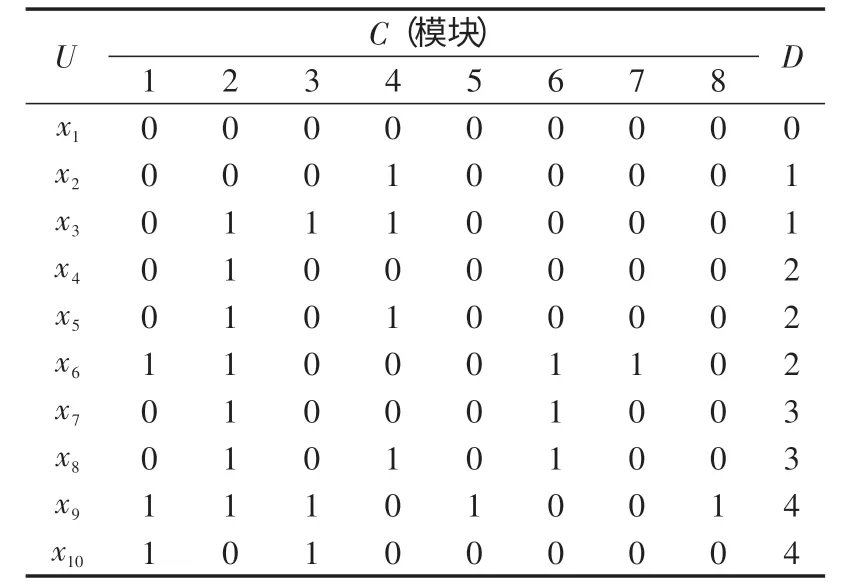
表1 预处理后的原始决策表Tab.1 Primitive decision table of using simplification method
Step1:计算原始决策表中的决策属性集D相对条件属性C的条件熵H(D|C)=0,可见本例为一致性决策系统。
Step2:计算得原始决策表的差别函数为:

另外,可得原始决策表的相对核为COREC(D)={2,3,4,6},令Att=C-CORED(C)={1,5,7,8}。
Step3:令RED=CORED(C)={2,3,4,6} ,对每个属性{1,5,7,8}分别计算H(D|RED ⋃{αi})。
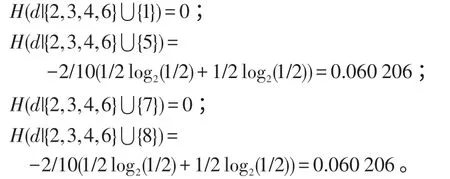
由于H(d|{2,3,4,6}⋃{1})=H(d|{2,3,4,6}⋃{7})=0 都达到最小,则在差别矩阵中统计出现次数,出现了18个“1”,7 个“7”,则选取出“1”,Att=Att-{1}={5,7,8},RED=RED ⋃{1}={1,2,3,4,6}。再跳到Step3 计算新一轮 的H(D|RED ⋃{αi}) ,条件熵都为0,则终止得REDC(D)={1,2,3,4,6}。
根据约简算法得新决策表如表2 所示,并将新决策表添加到诊断系统的规则表,如表3所示。
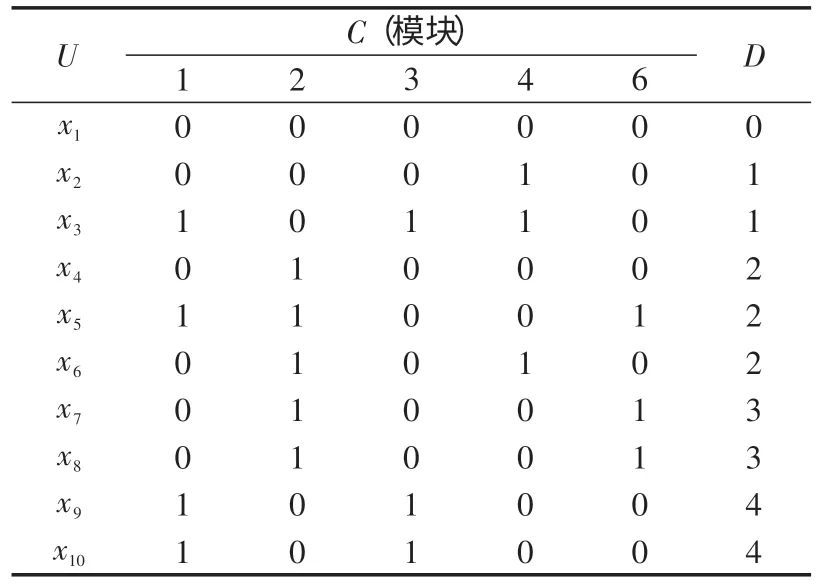
表2 新决策表Tab.2 New decision tables

表3 诊断结果Tab.3 Diagnosis result
经验证,基于改进的差别函数的属性约简算法与经典差别函数约简出的结果一致。但是从上例中不难看出,利用条件熵算法考虑到了条件属性与决策属性之间的关系,使得决策更加准确可靠。
3 结论
本文将条件熵算法应用于某型弹载数传电台设备的故障诊断中,验证表明结果与实际诊断相一致,具有一定的可靠性。同时,由于条件熵算法考虑了条件属性与决策属性之间的关系,弥补了差别函数和差别矩阵算法的不足,具有一定的应用价值。
[1] 苗夺谦,李道国.粗糙集理论、算法与应用[M].北京:清华大学出版社,2008:19-23,186-190.
MIAO DUOQIAN,LI DAOGUO. Rough sets theory and applications[M]. Beijing:Tsinghua University Press,2008:19-23,186-190.(in Chinese)
[2] PAWLAK Z. Rough setsp[J]. International Journal of Information and Computer Science,1982,11:341-356.
[3] 李岚.基于信息熵的属性约简及其应用[D].大连:大连海事大学,2008:119-123.
LI LAN. Attribute reduction methods and applications based on information entropy theory[D]. Dalian:Dalian Maritime University,2008:119-123.(in Chinese)
[4] KRYSZKIEWICZ M. Rules in incomplete information system[J].Information Sciences 1999,133:271-292.
[5] 植小三.基于粗糙集理论的数据挖掘模型及属性约简算法研究[D].重庆:重庆大学,2004:110-115.
ZHI XIAOSAN. The study on model of data mining and attribute reduction algorithm based on the rough set theory[D]. Chongqing:Chongqing University,2004:110-115.(in Chinese)
[6] 赵士亮. 粗糙集理论中若干问题的研究及应用[D]. 福州:福州大学,2003:93-99.
ZHAO SHILIANG. Study of several problems in rough set theory and its applications[D]. Fuzhou:Fuzhou University,2003:93-99.(in Chinese)
[7] 王国胤,姚一豫,于洪.粗糙集理论与应用研究综述[J].计算机学报,2009,7(36):1229-1231.
WANG GUOYING,YAO YIYU,YU HONG. A survey on rough set theory and applications[J]. Chinese Journal of Computers,2009,7(36):1229-1231.
[8] 林毅.基于粗集理论的关联规则挖掘的研究[D].柳州:广西大学,2004:77-84.
LIN YI.Association rule mining research based on rough set theory[D].Liuzhou:Guangxi University,2004:77-84.(in Chinese)
[9] 徐久成,孙林,马媛媛.基于新的条件熵的决策表约简方法[J].计算机工程与设计,2008,5(29):2313-2315.
XU JIUCHENG,SUN LIN,MA YUANYUAN. Reduction method of decision table based on new conditional entropy[J]. Computer Engineering and Design,2008,5(29):2313-2315.(in Chinese)
[10] 张文修,吴伟志.粗糙集理论介绍和研究综述[J].模糊系统与数学,2000,12(4):1-4.
ZHANG WENXIU,WU WEIZHI.An introduction and a survey for the studies of rough set theory[J]. Fuzzy Systems and Mathematics,2000,12(4):1-4.(in Chinese)
[11] STEFANOWSKI J,TSOUKIAS A. On the Extension of Rough Sets under Incomplete Information[J]. International Journal of Intelligent System,2000,16(1):29-38.
[12] FENTON B,MARTIN ME GINNITY,LIAM MAGUIRE. Fault diagnosis of electronic systems using artificial intelligence[J]. IEEE Instrumentation & Measurement Magazine,2002,(3):16-20.
[13]张光轶,苏艳琴,宋振宇.两种差别矩阵约简算法在故障诊断中的应用分析[J]. 中国电子科学研究院学报,2011,6(3):315-316.
ZHANG GUANGYI,SU YANQIN,SONG ZHENYU.Analysis of fault diagnosis based on the two discernibility matrix reduction algorithms[J]. Journal of China Academy of Electronics and Information Technology,2011,6(3):315-316.(in Chinese)

