一种基于径向加速度的Singer-EKF机动目标跟踪算法

贾舒宜，张赟

（海军航空工程学院a.电子信息工程系；b.飞行器工程系，山东烟台264001）

刘卫华

（海军航空工程学院科研部，山东烟台264001）

一种基于径向加速度的Singer-EKF机动目标跟踪算法

贾舒宜a，张赟b

（海军航空工程学院a.电子信息工程系；b.飞行器工程系，山东烟台264001）

针对雷达均不能提供目标加速度信息，在目标机动时会出现跟踪精度差甚至跟踪发散的问题，提出一种基于径向加速度的Singer-EKF算法。该算法在信号处理阶段利用Radon-Ambiguity变换（RAT）估计出目标的径向加速度，并通过坐标转换将其引入量测向量中，然后采用基于Singer模型的扩展卡尔曼滤波（EKF）算法实现机动目标的跟踪。仿真验证了该方法的有效性，并与传统的不带径向加速度的扩展卡尔曼滤波（EKF）方法进行了比较，结果表明该方法在径向距离、位置、加速度和速度估计精度方面都有所提高。

机动目标；径向加速度；扩展卡尔曼滤波；Singer模型；Radon-Ambiguity变换

机动目标跟踪一直是雷达、声纳和红外应用领域的难点。目前许多机动目标跟踪方法，主要是利用机动目标模型和滤波算法实现机动目标跟踪[1-8]。但现阶段雷达均不能提供目标加速度信息，因而在目标机动时会出现跟踪精度差甚至跟踪发散的问题。如果雷达在提供目标位置信息同时，也能够提供加速度信息，就可以提高机动目标的跟踪性能。

目前，关于信号处理阶段提取径向加速度的方法已有大量研究。当雷达发射恒定载频信号时，机动目标回波信号可近似看做线性调频（LFM）信号，径向加速度信息体现在雷达回波信号的调频率上，因而对雷达目标径向加速度估计就是对回波信号调频率的提取。目前，基于时频分析方法的LFM信号检测与估计技术不断出现。例如Wigner-Ville分布（WVD）[9]是一种常用的LFM信号检测估计方法，但在多目标情况下容易受交叉项的影响使得估计性能降低。为了解决这一问题，许多双线性变换的时频分析方法提出来，例如自适应chirplet变换（ACT）[10]、Radon-Ambiguity变换（RAT）[11]、分数阶傅里叶变换（FRFT）[12]等。其中，RAT的线性积分过程可以有效抑制交叉项干扰，并且计算量较小。因此，本文采用RAT方法在信号处理阶段估计目标径向加速度，再将径向加速度估计值进行坐标转换引入滤波算法的量测向量中，有效地提高了机动目标的跟踪精度。

本文采用Singer模型作为机动模型，原因在于Singer模型是一种典型的全局统计模型，兼顾了机动模型和非机动模型的精度。在目标跟踪系统中，本文采用了扩展卡尔曼滤波算法（EKF）实现了径向加速度量测到状态向量的转换。仿真验证了该方法的有效性，与传统的不带径向加速度量测的Singer-EKF方法相比，该方法的跟踪精度更高，并且在径向距离、方位角、加速度和速度估计精度方面也有所改善。

1 基于径向加速度的Singer-EKF算法

1.1 机动目标回波模型分析

假设脉冲多普勒雷达发射恒定载频信号，对于远距离单机动点目标，R(t)=R0+v0t+at2/2为其径向运动规律。这只考虑加速运动情况，忽略短时间内回波幅度的变化和距离徙动影响，其多普勒变化率为式（1）中：R0为目标到雷达的初始距离；λ为雷达发射信号波长；为初始速度，fd为多普勒频率；为目标径向加速度,k为目标加速度引起的多普勒变化率，可以看出其多普勒呈线性变化。

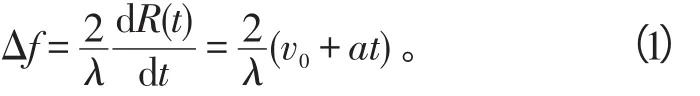
不考虑传播过程的衰减、低频调制及混进的噪声，回波可以看成一个线性调频信号。为了得到只与目标有关的频率信息，将信号与发射信号混频，并省略掉相位中的常量，回波信号可表示为

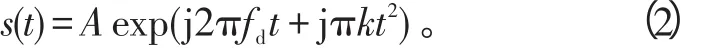
式（2）中：0≤t≤T，T为脉冲持续时间长度；A为个信号分量的幅度，这里假设为1。

由此可见，回波信号的调频率k包含了雷达的径向加速度a的信息，a的计算公式为

由式（3）可以看出，通过估计信号的调频率k就可得到目标的径向加速度。

1.2基于RAT的径向加速度估计

将持续时间有限的LFM信号（2）代入模糊函数定义中可得：

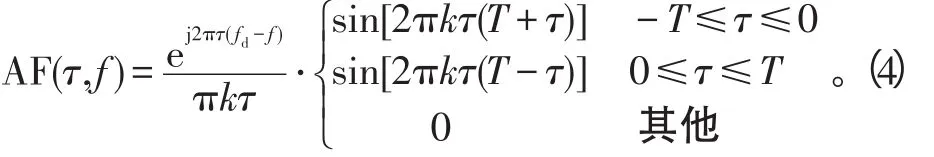
对于任意时刻τ∈(-T,T)，AFs(τ,f)在f=kτ处取最大值，其模糊函数呈背鳍状，模糊函数及在时延—频移平面上的投影分别如图1和图2所示。由此可见，对于有限长的线性调频信号在时延—频移平面上投影为过原点的一条直线f=kτ。由于有限长的线性调频信号的模糊函数为过原点的一条直线，而Radon变换具有沿直线积分累加的作用，因此我们将两者结合，采用|AFs(τ,f)|在模糊平面(τ,f)上沿通过模糊原点的θ角方向的直线进行积分，得到的结果即为Radon-Ambiguity变换[11]，即：

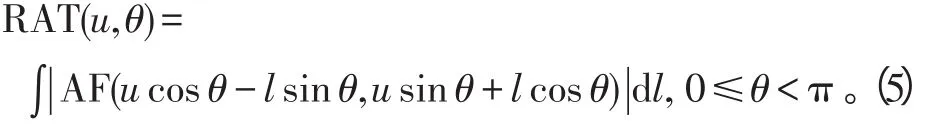
当沿直线f=kτ（图2）作直线积分时，只需考虑搜索角度θ。因而对信号的模糊图进行Radon变换时，可以把RAT(θ)看成关于搜索角度θ的线性累加器，只须进行关于θ的一维搜索：

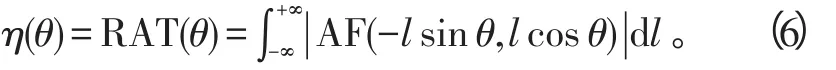
经过一系列搜索角度θ的计算和积累，最后在二维平面上出现一个峰值，这个峰值对应的角度θ，就是估计调频率所需的角度θ。径向加速度估计具体步骤如下：

1）回波信号序列为

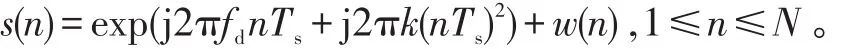
N为序列长度，A是信号的幅度，采样周期为Ts，w(n)为均值为零方差为σ2的高斯白噪声。

2）计算s(n)的模糊函数AF(τ,f)，并求出模|AF(τ,f)。

3）对||AF(τ,f)进行Radon变换，并且进行关于θ的一维搜索，并求得峰值对应的θ角。

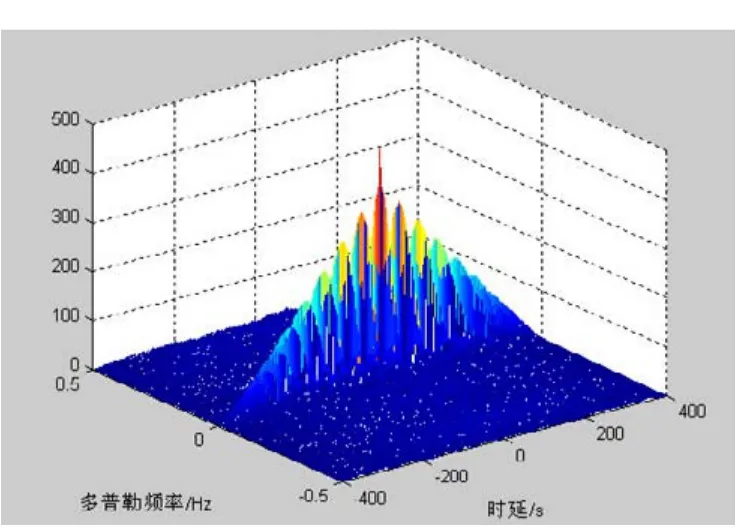
图1模糊函数图Fig.1 Ambiguity function

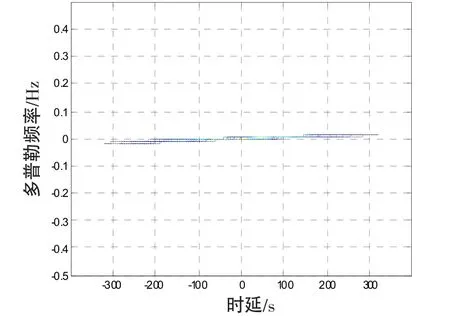
图2模糊函数投影图Fig.2 Projection of ambiguity function

1.3 状态方程

状态方程是由目标的运动模型决定的，基于Singer模型的状态方程可以表示为

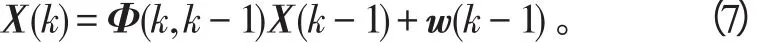
式（7）中，状态向量

xk、x˙k、x¨k和yk、y˙k、y¨k分别表示k时刻目标x方向和y方向的位置、速度、加速度。

状态转移矩阵

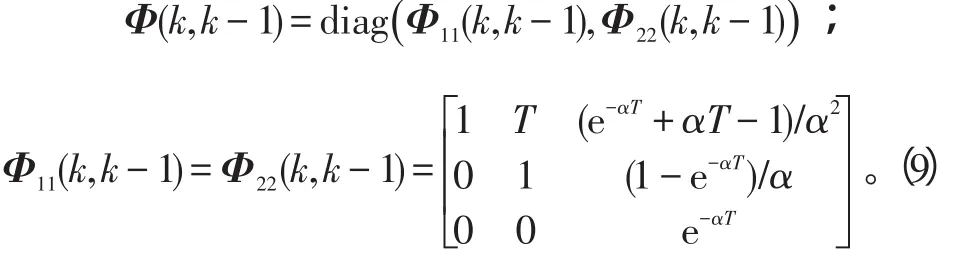
式（9）中：α为机动时间常数；T为采样周期。其离散时间过程噪声w具有协方差：

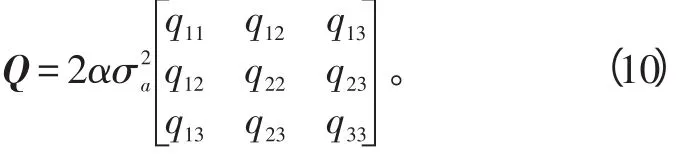
式（10）中,Q精确表达式为：

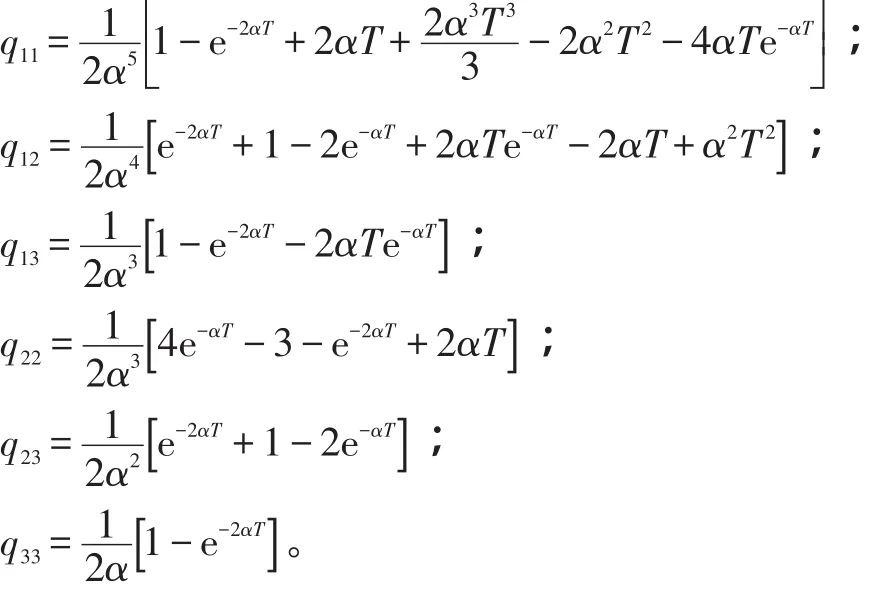
1.4 量测方程

设雷达在极坐标系下位置量测（距离和方位角）、径向速度量测和径向加速度量测分别为zρ、zφ和za，则

式（11）中：ρ、φ和a分别表示目标距离、方位角和径向加速度的真值；和分别表示方差为σ2ρ、σ2φ和σ2a的零均值高斯白噪声。

非线性量测方程为

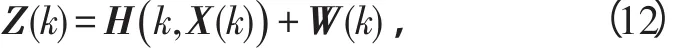
式中：Z(k)表示量测向量；H表示非线性量测转移矩阵；W(k)表示方差为R(k)的高斯白噪声。

量测矩阵

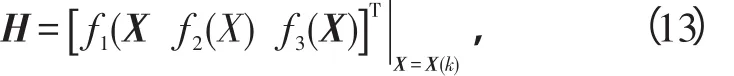
式中：

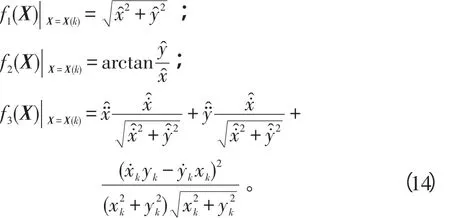
量测噪声协方差

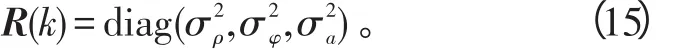
2 仿真验证

在仿真过程中，假设雷达波长为λ=8mm，雷达在信号处理阶段采样间隔为Ts=5×10-5s，观测时间为T=50 ms，信噪比为SNR=0 dB，RAT算法中，搜索步长为Δθ=0.125°，搜索半径为Δρ=1.1Ts。雷达在数据处理阶段采样间隔为T′s=1 s，距离量测误差为ρr=100 m，角度量测误差为ρφ=0.5°，加速度测量误差为ρa=1 m/s2，目标的起始状态为目标运动过程历时90 s，目标发生机动时刻及加速度见表1，目标直角坐标系下运动轨迹如图3所示。

表1目标机动运动情况表Tab.1 Movement of maneuvering target

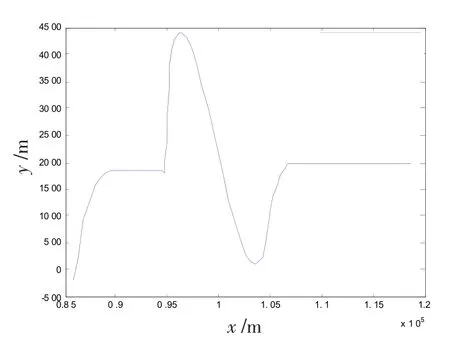
图3目标运动轨迹Fig.3 Trajectory of the target

由上述条件下得到信号模型为

式中，w(t)为均值为1的高斯白噪声。在信号处理阶段利用RAT方法得到目标径向加速度估计，估计值结果如图3和图4所示，并将其作为量测向量中径向加速度量测值。在数据处理阶段，利用Singer模型和EKF算法对目标进行跟踪，结果如图5～12所示。从仿真结果中可以看出，目标跟踪精度明显提高，原因在于径向加速度的引入增加了量测向量的维数，因而提高了跟踪性能，同时目标位置、加速度和速度的估计精度也有明显改善。由图5～12还可以看出，在x轴方向的跟踪精度要明显优于y方向的跟踪精度。这是由于当目标处于不同位置时引入径向加速度对跟踪精度影响程度是不一样的，目标跟踪精度的改善效果与其所处位置有关，目标越靠近的哪个坐标轴方向，哪个轴的跟踪精度越高。

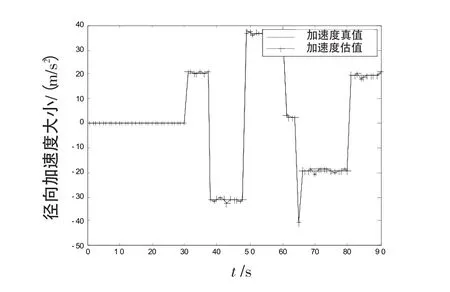
图4径向加速度真实和估计值Fig.4 True values and estimations of radial acceleration

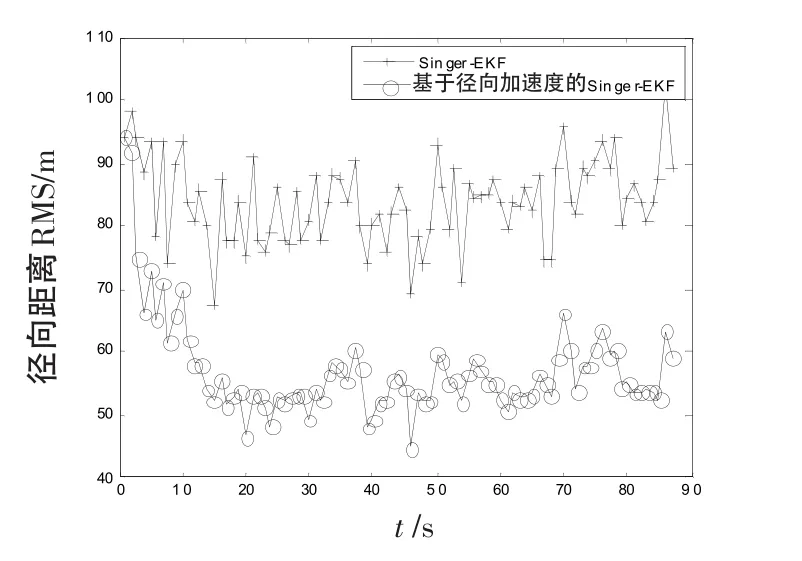
图5径向距离误差曲线Fig.5 Error curve of radial range

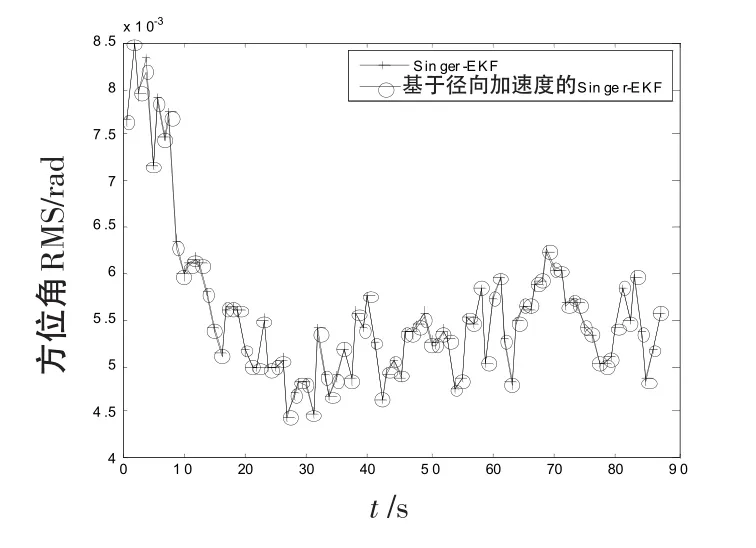
图6方位角误差曲线Fig.6 Error curve of bearing

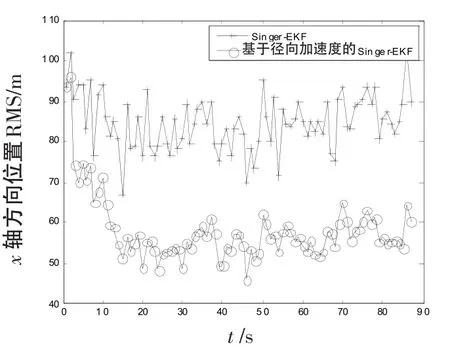
图7x轴位置误差曲线Fig.7 Error curve of position inxaxis

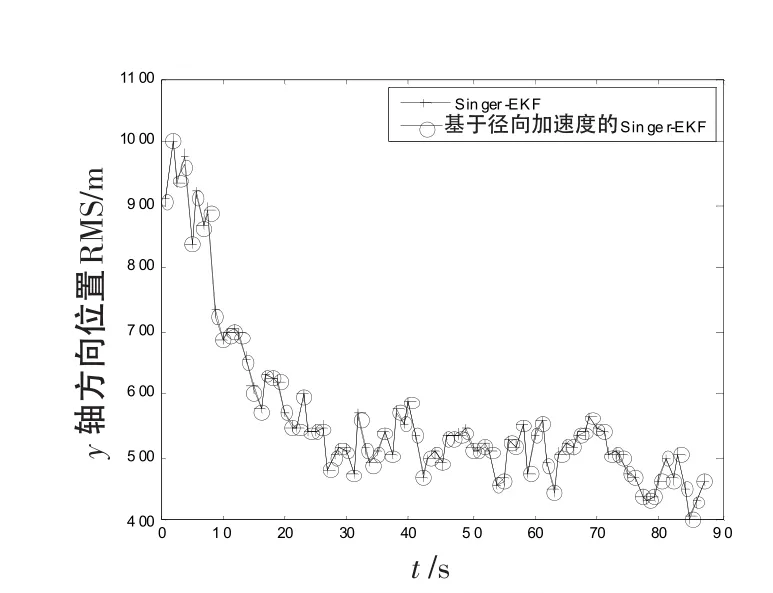
图8y轴位置误差曲线Fig.8 Error curve of position inyaxis

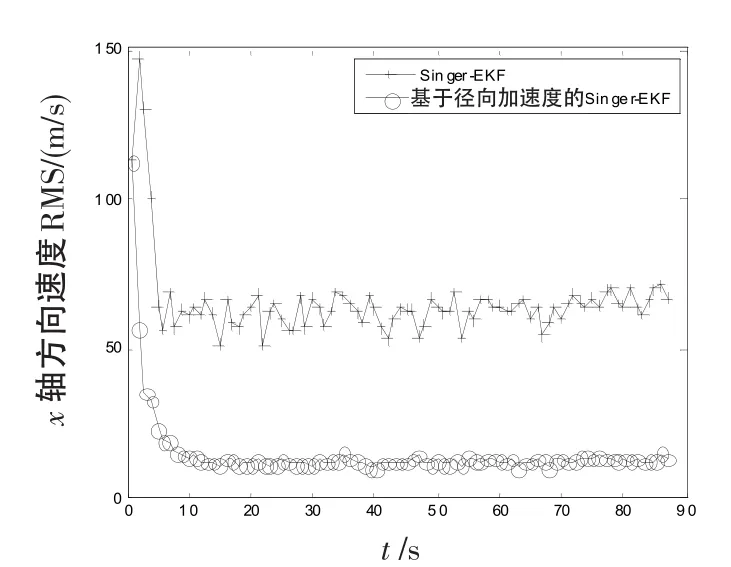
图9x轴速度误差曲线Fig.9 Error curve of velocity inxaxis

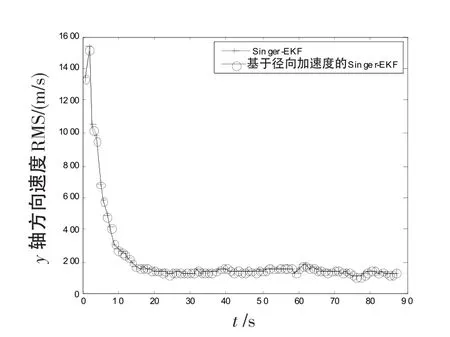
图10y轴速度误差曲线Fig.10 Error curve of velocity inyaxis

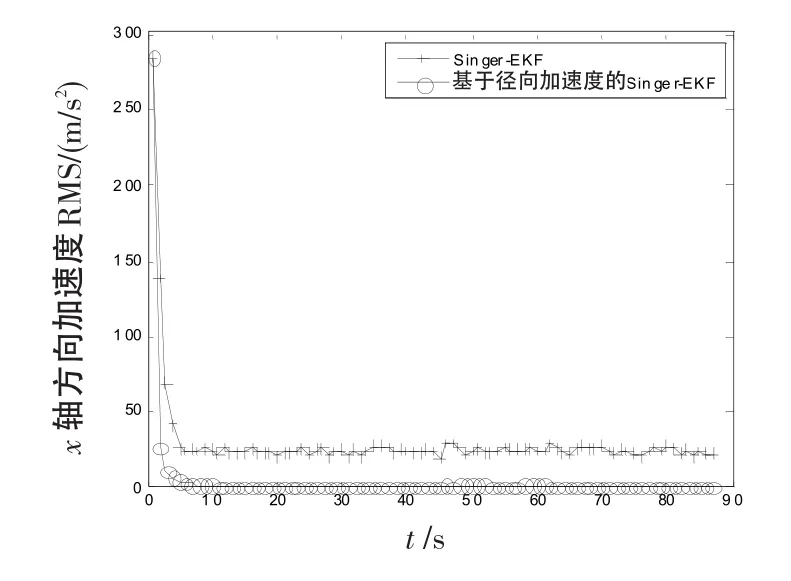
图11x轴加速度误差曲线Fig.11 Error curve of acceleration inxaxis

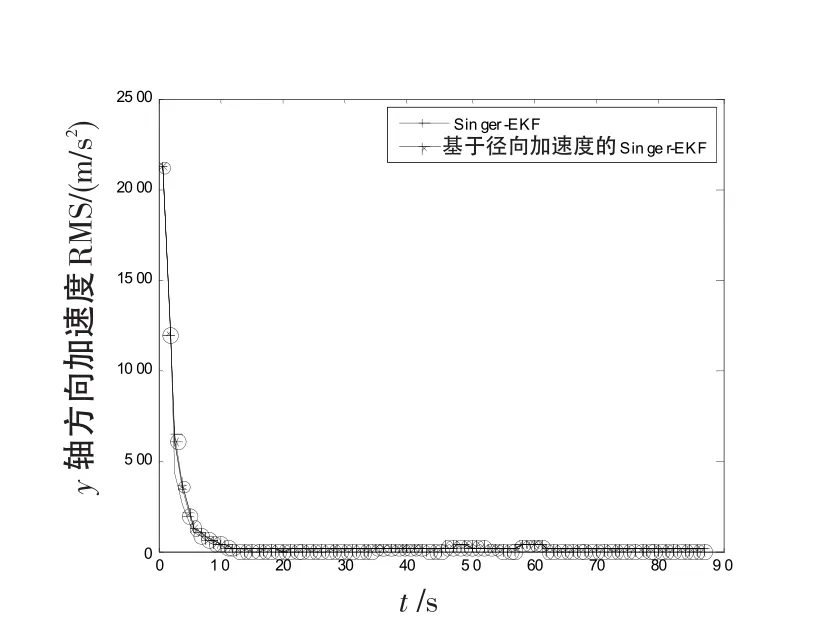
图12y轴加速度误差曲线Fig.12 Error curve of acceleration inyaxis

3 结论

本文提出一种带径向加速度的Singer-EKF机动目标跟踪算法。由于径向加速度是在信号处理阶段利用RAT方法能精确地提取出来的，因而将其引入测量向量可提高机动目标跟踪精度。仿真结果验证了该方法在机动条件下的跟踪效果要优于传统的Singer-EKF算法。利用该方法的研究成果，可以在雷达提供目标位置和速度信息的同时，提供目标的径向加速度信息，从而实现对机动目标的精确跟踪。

[1]TIMOTHY L MOLLOY，JASON J FORD.HMM triangle relative entropy concepts in sequential change detection applied to vision-based dim target maneuver detection[C]//15th International Conference on Information Fusion.Singapore：Interational Society of Information Fusion，2012：1120-1125.

[2]GAO L，XING J P，MA Z L.Improved IMM algorithm for nonlinear maneuvering target tracking[J].Proedia Engineering，2012，29（6）：4117-4123.

[3]FANTACCI C，BATTISTELLI G，CHISCI L，et al.Multiple-model algorithms for distributed tracking of a maneuvering target[C]//15th International Conference on Information Fusion.Singapore：Interational Society of Information Fusion，2012：1231-1235.

[4]JIAO LIANMENG，PAN QUAN，LIANG YAN，et al.A nonlinear tracking algorithm with range-rate measurements based on unbiased measurement conversion[C]// 15th International Conference on Information Fusion.Singapore：Interational Society of Information Fusion，2012：1400-1405.

[5]PENG D L，GU Y.IMM algorithm for a 3D high maneuvering target tracking[J].Lecture Notes in Computer Science，2011，6729（1）：529-536.

[6]GAO CAICAI，CHEN WEI.Ground moving target tracking with vs-imm using mean shift unscented particle filter [J].Chinese Journal of Aeronautics，2011，24（5）：622-630.

[7]XIA X G.Discrete chirp-fourier transform and its application to chirp rate estimation[J].IEEE Transactions on signal processing，2000，47（11）：3122-3133.

[8]YANG X J，XING K Y，FENG X L.Maneuvering target tracking in dense clutter based on particle filtering[J]. Chinese Journal ofAeronautics，2011，24（2）：171-180.

[9]KUMAR K ANOOP，ARVIND MANOJ，DIVAKAR K，et al.A novel time-frequency approach for acceleration estimation from a single PR[C]//Fifth International Symposium Signal Processing and it’s applications.Brisbane：Signal Processing Research Centre，1999：531-534.

[10]XIA X G.Discrete chirp-fourier transform and its application to chirp rate estimation[J].IEEE Transactions on signal processing，2000，47（11）：3122-3133.

[11]孙军海，李亚超，刑蒙道，等.基于Radon-Ambiguity变换的多目标检测[J].西安交通大学学报，2009，43（4）：81-89. SUN JUNHAI，LI YACHAO，XING MENGDAO，et al. Detection of multiple targets based on radon-ambiguity transformation[J].Journal of Xi’an Jiaotong University，2009，43（4）：81-89.（in Chinese）

[12]杜文超，王国宏，高学强.低信噪比条件下在短时信号中提取目标径向加速度方法研究[J].中国科学：技术科学，2007，37（7）：923-943. DU WENCHAO，WANG GUOHONG，GAO XUEQIANG.Acceleration estimation from short time duration in low SNR[J].Science China：Technology Scinces，2007，37（7）：923-943.（in Chinese）

JIA Shu-yia,ZHANG Yunb

（Naval Aeronautical and Astronautical university a.Department of Electronic and Information Engineering; b.Department of Airborne Vehicle Engineering,Yantai Shandong 264001,China）

海杂波中广义符号恒虚警检测算法性能分析

刘卫华

（海军航空工程学院科研部，山东烟台264001）

摘 要：分析了广义符号检测算法在仿真的高斯杂波背景和实测海杂波背景下，对2种目标（Swerling 0型和Swerling II型）的检测性能，以及对实际渔船目标的检测性能。研究表明，随着脉冲数、参考单元数和信杂比的提高，该检测算法的检测性能有所提高；在低信杂比条件下，GS检测算法对Swerling II型目标的检测性能优于对Swerling 0型目标的检测性能，在高信杂比的条件下，对Swerling 0型目标的检测性能优于对Swerling II型目标的检测性能。

关键词：非参量；广义符号；海杂波；信杂比

在复杂的噪声背景下保持恒定的虚警概率是设计目标检测算法必须考虑的问题[1]。当杂波包络分布类型已知时，通过采集数据来估计某些参数，从而对信号进行有效的检测，这种检测方法被称为参量检测方法。然而，如果实际杂波分布和假设差距较大，检测性能就会大幅下降。因此，设计虚警概率与背景分布无关的检测算法很有必要，这种检测算法被称为非参量检测算法。在背景分布已知的情况下，非参量检测算法的性能往往不如参量检测算法，但是在背景分布未知的情况下，非参量检测算法的性能往往好于参量检测算法[2]。在雷达实际工作环境当中，杂波分布类型往往无法准确预知，因而非参量检测方法受到越来越广泛的关注[3-5]。常见的非参量检测算法有符号检测算法[6]，Wilcoxon检测算法[7]，广义符号（GS）检测算法[2]和Mann-Whitney检测算法[8]。GS检测算法处理的是经包络检波器输出的回波信号，将检测单元与周围参考单元进行比较，并得到相应的非参量化检验统计量[7]，是易实现的两样本非参量检测算法之一。

为了研究GS检测算法对不同类型目标的检测性能，本文在仿真杂波数据、实测海杂波环境中，对GSCFAR检测算法的检测性能和海杂波抑制能力进行了仿真分析。由于GS检测算法的性能与脉冲数和参考单元数有关[2]，因而本文还研究了脉冲数和参考单元数对GS检测算法性能的影响。

1 算法模型

1.1 GS检测算法原理

GS检测算法是对接收信号进行多脉冲检测的两样本符号检测算法。该算法将检测单元的幅度值与周围参考单元的幅度值进行比较，得到检测单元的检验统计量，再将检验统计量与对应的检测阈值比较。图1给出了GS检测算法的原理框图[7]，检测单元采样用yj(j=1,2,…,N)，参考单元采样xji(i=1,2,…,M)。检测单元两侧各有一个保护单元，防止检测单元中可能的目标信号泄漏到邻近的参考单元中而影响检测。

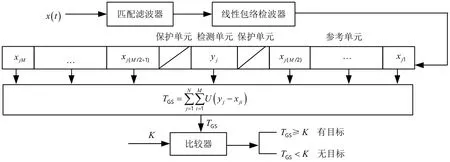
图1 GS检测算法原理框图Fig.1 Schematic diagram of GS detection algorithm

检验统计量

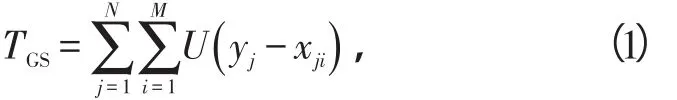
式中：U(·)是单位阶跃函数；N为脉冲数；M为参考单元数。

将检验统计量TGS和检测阈值K进行比较，如果TGS≥K，则判决存在目标；如果TGS＜K，则判决不存在目标。在无目标条件下，假设yj满足独立同分布；在有目标条件下，假设yj和xji满足独立同分布[2]。

1.2 检测阈值K的确定

虚警概率Pfa可根据脉冲数N、参考单元数M和检测阈值K的大小来设定[2]，因而Pfa的值可以N、M和K进行函数表示，具体关系如式（2）所示：

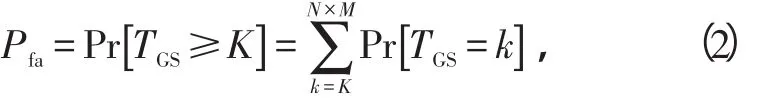
式中，

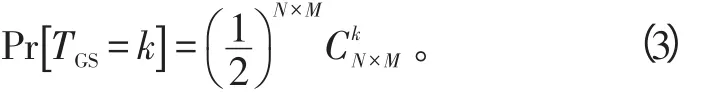
从式（2）可以看出，Pfa不依赖于杂波和噪声的分布形式，只与K、N和M有关，因而GS检测算法可使虚警概率保持恒定[7]。

当Pfa、N和M已知时，K可以由Pfa反解出来，那么K也不依赖于杂波和噪声的分布形式。当Pfa=10-4、N=10、M=16时，根据上述公式得出K=127。

2 GS检测算法性能分析

2.1 仿真杂波+目标回波条件下的性能分析

本节采用高斯分布来模拟产生海杂波。分别产生I、Q2路标准高斯分布（均值为0，方差为1）序列，求包络后作为背景杂波数据。

产生不起伏Swerling 0型目标回波和快起伏Swerling II型目标回波，将其与杂波数据合成，并调整信杂比（SCR）。

信杂比的计算公式为

当SCR已知时，可以根据上式反推出目标信号的幅度，从而计算出在不同信杂比情况下的检测概率[9]。

图2给出了Pfa=10-3，脉冲数和参考单元数分别改变时，2种目标模型条件下，SCR与检测概率关系曲线。

图2基于仿真数据的检测概率与信杂比关系曲线Fig.2 Relationship curve of detection probability and SNR based on simulated data

由图2可以看出：

1）当脉冲数和参考单元数一定，信杂比在一定范围内变化时，检测概率随着信杂比的增大而不断增大；

2）在信杂比和参考单元数一定的条件下，随着脉冲数的增大，检测概率有所增大；

3）在信杂比和脉冲数一定的条件下，随着参考单元数的增加，检测概率有所增大；

4）脉冲数变化对检测Swerling 0型目标和Swerling II型目标的影响要强于参考单元数对检测2种目标的影响；

5）在低信杂比条件下，GS检测算法对Swerling II型目标的检测性能优于对Swerling 0型目标的检测性能；在高信杂比条件下，对Swerling 0型目标的检测性能优于对Swerling II型目标的检测性能。

2.2 真实杂波+仿真目标回波条件下的性能分析

为进一步验证不同参数对GS检测算法性能的影响情况，本节基于某实测数据对GS检测算法性能进行分析，实际海杂波背景较为复杂，且分布类型一般是未知的。设Pfa=10-3，杂波数据是通过雷达采集得到的，目标类型仍采用Swerling 0型和Swerling II型。图3给出N和M分别变化时，2种目标模型的SCR与检测概率的对应关系曲线。

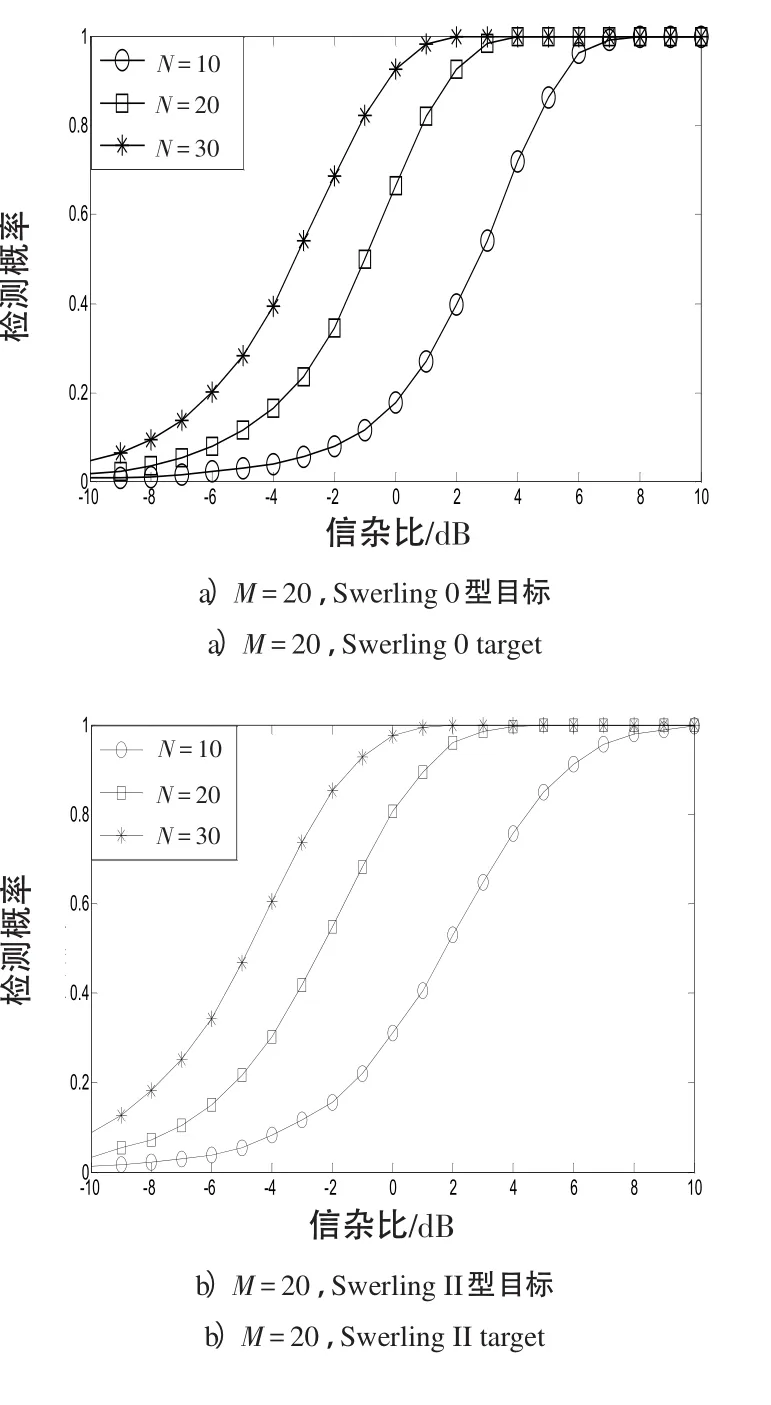
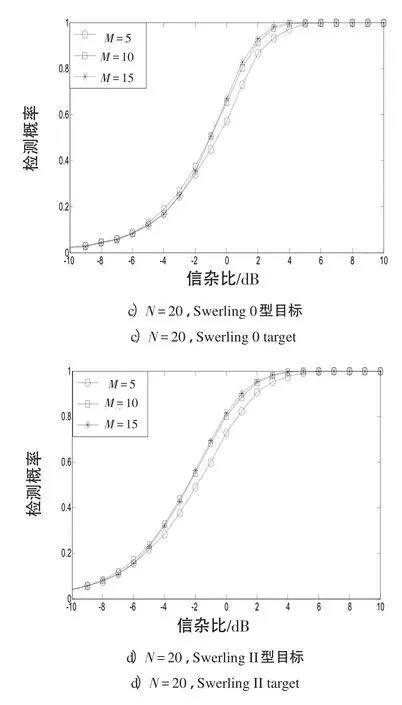
图3基于实测数据的检测概率与信杂比关系曲线Fig.3 Relationship curve of detection probability and SNR based on real data

由图3可以看出：

1）在其他条件相同的情况下，检测概率随脉冲数的增大而有所增大。对于实测数据，在高信杂比条件下，对Swerling 0型目标的检测能力优于对Swerling II型目标的检测能力；在低信杂比条件下，对Swerling II型目标的检测能力优于对Swerling 0型目标的检测能力；

2）在其他条件相同的情况下，检测概率随着参考单元数的增大而有所增大，但变化不明显；

3）脉冲数变化对检测Swerling 0型目标和Swerling II型目标的影响要强于参考单元数对检测Swerling 0型目标和Swerling II型目标的影响。

上述分析进一步说明，GS检测算法是一种与杂波分布类型无关的检测方法，即在不同的杂波分布类型情况下，几种参数对非参量检测算法性能的影响趋势保持一致。

分析原因：

1）Swerling II型目标为快起伏目标，脉冲和脉冲间的起伏是统计独立的，若前一个脉冲没有超过门限，则相继脉冲有可能超过门限；而不起伏目标的相关性较强，如果第一个脉冲振幅小于检测门限，则相继脉冲也不会超过门限。在低信杂比条件下，信号幅度较低，快起伏目标经过检测算法处理之后得到的检验统计量超过检测阈值的概率相对较大而更容易被检测到；在高信杂比条件下，信号幅度相对较大，相对稳定的不起伏目标经过检测算法处理之后得到的检验统计量要高于快起伏目标，从而更容易被检测到；

2）GS检测算法将检测单元和周围的参考单元进行比较以得到检验统计量，其本质是对目标优势的积累。若增大脉冲数，则在脉冲间相对稳定的有用信号的优势可得到进一步的积累，检测效果会明显改善。

2.3 真实杂波+真实目标回波条件下的性能分析

本节基于雷达对海上目标检测的实测数据进行分析，以验证GS检测算法对渔船目标的检测性能。图4给出了虚警概率Pfa=10-3、脉冲数N和参考单元数M分别变化时的二维平面图。图4中纵坐标表示距离单元，横坐标表示重复扫描的次数，每一个像素点表示一次扫描的回波强度[10]，图4 a）为原始数据平面图，图4 b）～d）为GS检测算法处理后的显示结果。

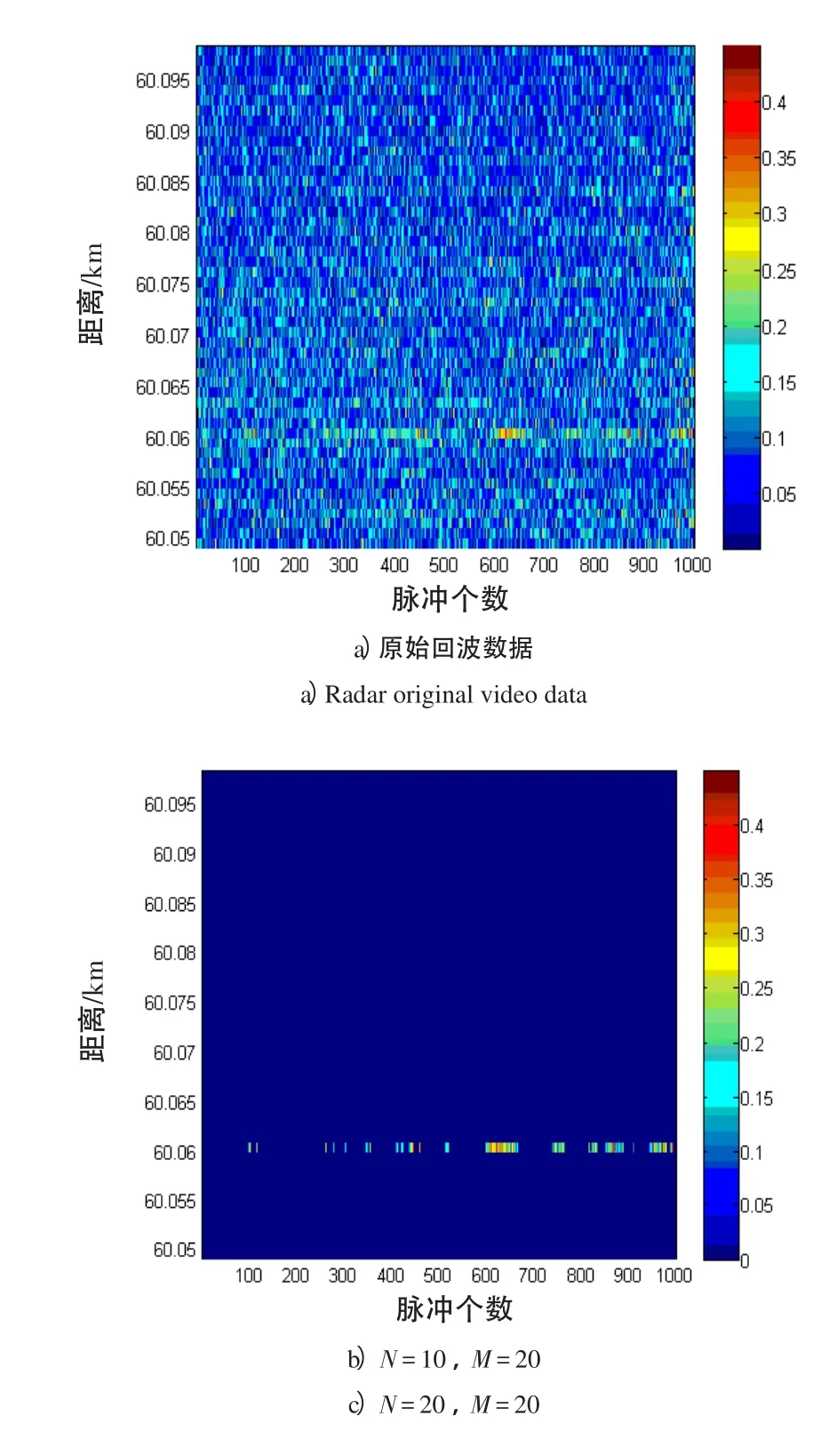
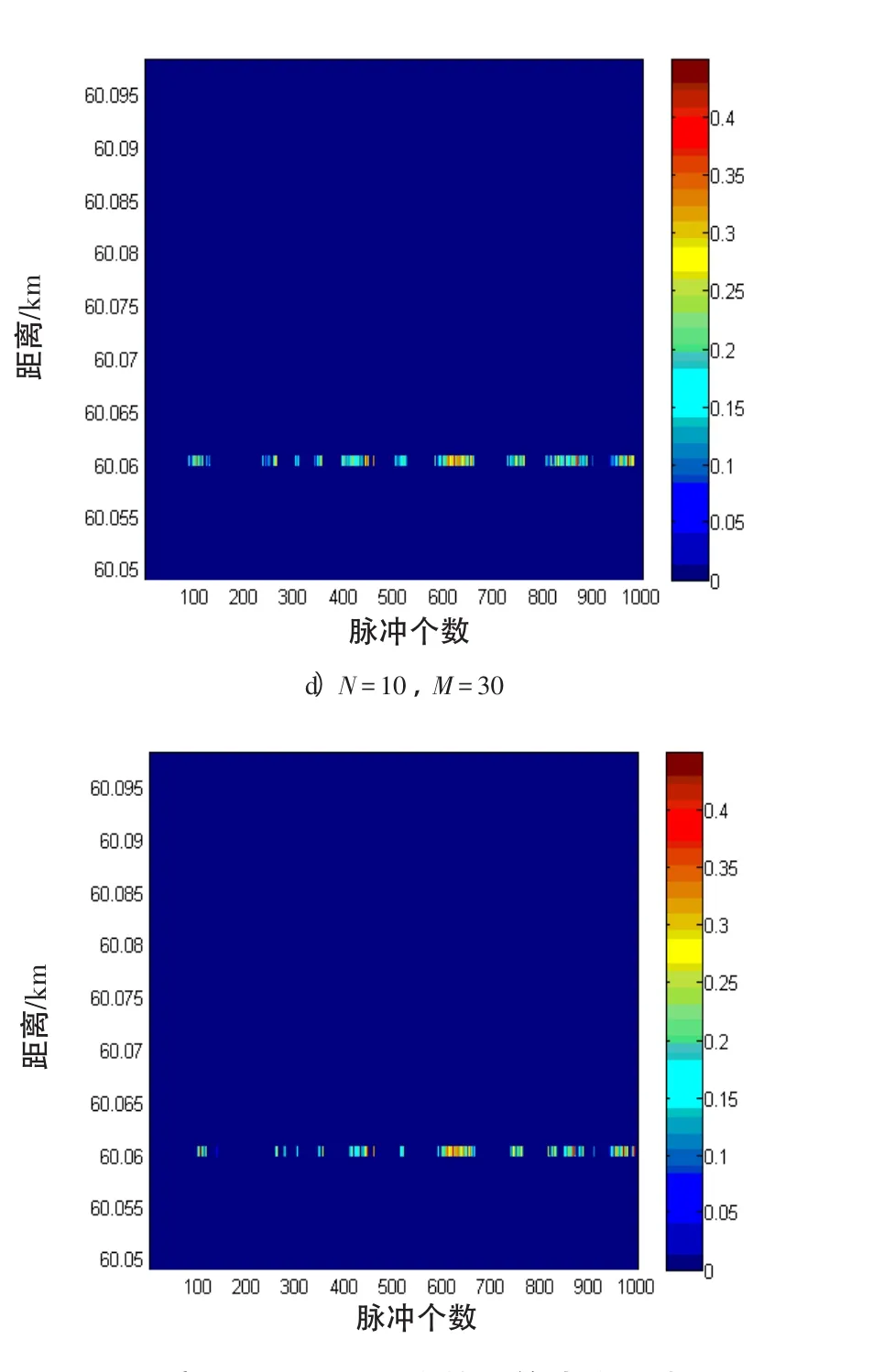
图4实测数据显示图和检测算法处理结果Fig.4 Radar original video data and the result of detection algorithm

由图4 a）可知，在60 km处有1个渔船目标湮没在海杂波当中，较难分辨；经过GS检测检测算法处理后的结果如图4 b）～d）所示，绝大部分杂波被抑制掉，画面非常清晰。从图4可以看出：

1）相比于原始数据平面图，GS检测算法成功检测出了目标，该检测算法对杂波有很好的抑制作用。当N增大时，颜色不一的间断条状回波逐渐变为连续的条状回波；

2）对于1 000次观测，当M为20，N为10时，检测到目标259次；当M为20，N为20时，检测到目标422次；当M为30，N为10时，检测到目标272次。由此可知，随着脉冲数N的增多检测效果明显变好，但参考单元数M对检测效果的影响并不明显。

3 总结

本文利用Swerling 0和Swerling II型目标回波叠加仿真杂波和实测海杂波数据，研究了不同参数，即信杂比、参考单元数和脉冲数对GS检测算法性能的影响，并采用真实海杂波+目标回波数据进行验证。结果表明：

1）在高斯杂波背景和实测海杂波背景下，随着脉冲数、参考单元数和信杂比的增大检测概率不断增大，但脉冲数对检测概率的影响强于参考单元数对检测概率的影响；在高信杂比条件下，对Swerling 0型目标的检测能力优于对Swerling II型目标的检测能力；在低信杂比条件下，对Swerling II型目标的检测能力优于对Swerling 0型目标的检测能力。

2）通过对实测数据验证表明，GS检测算法可以检测到海杂波中的渔船，在虚警概率保持不变的条件下，随着脉冲数和参考单元数的增大，算法的检测性能得到改善，但是参考单元数对检测性能的影响并不明显。

参考文献：

[1]马克·理查滋.雷达信号处理基础[M].3版.北京：电子工业出版社，2008：260-286. MARK A RICHARDS.Fundamentals of radar signal processing[M].3rd ed.Beijing：Publishing House of Electronics Industry，2008：260-286.（in Chinese）

[2]VILHELM GREGERS HENSEN.Nonparametic radar extraction using a generalized sign test[J].IEEE Transactions on Aerospace&Electronic Systems，1971，7（5）：941-950.

[3]SEYEF B，SHARAFAT A R.Signed-rank nonparametric multiuser detection in non-gaussian channels[J].IEEE Transactions on Information Theory，2005，51（4）：1478-1486.

[4]HAO CHEN.Noise enhanced nonpatametric detection[J]. IEEE Transactions on Information Theory，2009，55（2）：499-506.

[5]ORTON M.Nonparametric rank detectors under k-distributed clutter in radar application[J].IEEE Transactions on Aerospace&Electronic Systems，2005，41（2）：702-710.

[6]CARLYLE J W.On nonparametric siganl detectors[J]. IEEE Transactions on Information Theory，1964，10（2）：146-152.

[7]何友，关键.雷达目标检测与恒虚警处理[M].2版.北京：清华大学出版社，2011：230-250. HE YOU，GUAN JIAN.Radar target detection and cfar processing[M].2rd ed.Beijing：Tsinghua University Press，2011：230-250.（in Chinese）

[8]ZEORI G W.Performance of a two-sample mann-whitney nonparametric detector in a radar application[J]. IEEE Transactions on Aerospace&Electronic Systems，1971，7（5）：951-959.

[9]赵志坚.海杂波中非参量恒虚警检测算法性能分析[J].雷达科学与技术，2010，8（1）：65-73. ZHAO ZHIJIAN.Performance analysis of nonparametric CFAR detectors in sea clutter[J].Radar Science and Technology，2010，8（1）：65-73.（in Chinese）

[10]张林.三种两样本非参量检测器CFAR检测算法分析[J].海军航空工程学院学报，2011，26（3）：296-300. ZHANG LIN.Performance analysis of three kinds of twosample nonparametric CFAR detectors[J].Journal of Navel Aeronautical and Astronautical University，2011，26（3）：296-300.（in Chinese）

Abstract:The performance of GS detector for two kinds of target（Swerling 0 and Swerling II）was studied under Gaussian clutter and real sea clutter.The analysis results showed that，with the numbers of pulse，reference cells and signal-toclutter ratio（SCR）increasing，the performance of GS detector rose.In the condition of low SCR，the performance of GS detector detecting Swerling II targets was better than that of GS detector detecting Swerling 0 targets;and in the condition of high SCR，the performance of GS detector detecting Swerling 0 targets was better than that of GS detector detecting Swerling II targets.

Key words：nonparametric;generalized sign;sea clutter;SCR

Tracking Algorithm of Singer-EKF Maneuvering Target Based on Radial Acceleration

The performance of maneuvering tracking can be improved if acceleration is derived.Therefore,a Singer-EKF method based on Radon-Ambiguity transformation(RAT)was proposed for enhancing the tracking of a maneuvering target.In the proposed method,the radial acceleration was derived based on Radon-Ambiguity transformation in signal processing and then brought into the measurement vector coordinates transform model.In the filtering approach,a method of Extended Kalman Filter(EKF)based on Singer model was adopted to resolve the problem of the non-linearity of the measurement equation.The tracking performance of the proposed method is evaluated and compared with the traditional Extended Kalman Filter(EKF)algorithm based on the Singer model without acceleration measurement.It is showned that the proposed algorithm outperformed better in maneuvering scenario,and the estimate accuracies of radial distance,position, acceleration and velocity were improved at the same time.

maneuvering target;radial acceleration;EKF;Singer model;Radon-Ambiguity transformation

Performance Analysis of Generalized Sign CFAR Detection Algorithms Within Sea Clutterr

LIU Wei-Hua
（Department of Scientific Research，NAAU,Yantai Shandong 264001,China）

TN911.23

A

1673-1522（2014）02-0141-05

10.7682/j.issn.1673-1522.2014.02.009

TN957文献标志码：A

��编号：1673-1522（2014）02-0146-05DOI:10.7682/j.issn.1673-1522.2014.02.010

2013-10-09；

2014-02-12

国家自然科学基金资助项目（61102165；61102167）

贾舒宜（1984-），女，博士。

收稿日期：2013-12-16；修回日期：2014-02-10

基金项目：国家自然科学基金资助项目（61002045，61179017，61201445，61302008）

作者简介：刘卫华（1973-），男，讲师，硕士。