一种基于SRT-8算法的SIMD浮点除法器的设计与实现*
邓子椰,陈书明,彭元喜,雷元武
(国防科学技术大学计算机学院,湖南长沙410073)
1 引言
浮点除法运算是基本操作之一。在早期的计算机中,除了除法本身的复杂性外,除法的不频繁使用导致了人们对除法效率的忽略。随着VLSI技术的发展,针对各个应用领域的处理器相继出现,特别是DSP、MMP等专用处理器,这些处理器的应用需求使得除法应用越来越广泛;而通用处理器中也大部分实现了浮点除法,如AMD-K7、Intel Core i7和Intel Itanium[1]等等。同时,各种应用的处理器对计算速度、芯片面积以及功耗大小的要求也对除法的实现提出了挑战,因此设计并实现高速低开销的浮点除法器是十分重要的。
除法算法可以分为三类:查表法、函数迭代和数字迭代。查表法使用简单,当精确度要求不高时可以直接用其得到结果,但对于IEEE-754标准的单精度浮点除法,很难使用查表法直接实现精确的浮点除法。函数迭代算法包括Newton-Raphson和Goldschmidt算法,这类算法具有收敛速度快的特点,通常与查表法相结合使用来降低迭代次数。函数迭代算法每次迭代都涉及到多次乘法操作,所以需要较大的乘法器,面积较大。例如AMD处理器[2]、NVIDIA GPUs[3]、Intel Itanium CPUs[4]及FT-matrix。数字迭代方法是基本函数实现中最广泛的一类算法。它以简单的加减法和移位操作为基础,每次迭代获得固定位数的商。在目前的处理器中,使用最多的数字循环算法是SRT(Sweeney、Robertson以及Tocher)[5],使用SRT-4算法的处理器有Intel Pentium CPUs[6]、ARM处理器[7]和IBM FPUs[8];Intel Core2处理器实现SRT-16除法[6]。
本文基于SRT-8除法算法,设计了一种输入输出皆符合IEEE-754浮点标准的SIMD(Single Instruction Multiple Data)浮点除法器,支持一个双精度或两个并行单精度浮点除法。在深入研究SRT除法算法基础上,通过优化SRT-8迭代除法结构,提出商选择和余数加法的并行处理,并采用商数字存储技术来降低迭代除法的计算延时,提高频率。另外,SIMD结构采用复用策略减少硬件资源开销,节省面积。
2 SRT算法及基数选择
SRT算法基于以下关系式:

其中,Pj+1是第j次循环之后的部分余数;P0为最初的除数;r是SRT算法的基;d表示被除数;qj+1表示第j次循环得到的商。
SRT算法的关键是基数的大小,它决定了每次循环可以得到的商的位数,每次迭代得到的位数越多则需要迭代的次数就越少,除法运算所需的周期就越少,从而可提高算法性能。但是,增大基数会增加设计的硬件复杂度,同时也会增加除法部件的延迟和面积。Oberman S F[1]指出查找商选择函数表所需要的时间延迟与基数成线性增长,而所需要的面积与基数成二次方增长。文献[9]通过实验结果表明,基4优化结构比传统结构减少的时间最短;基8优化结构选择表的查找电路和函数选择表输入值的计算电路相对比较平衡,减少的时间延迟最大;基16实现选择表输入值的计算电路过于复杂,减少的时间延迟介于前两者之间。
商数字选择函数定义如下:
qj+1=k∈+1,…,0,…,a-1,a},收敛条件d(k-ρ)≤rPj≤d(k+ρ),在PD图中r Pj表示为P,d表示为D,则:
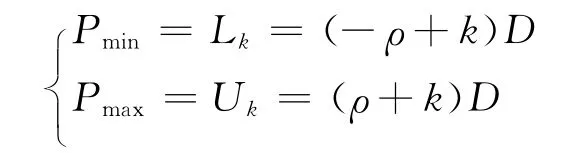
我们取r=8,a=5为例,如图1所示。

Figure 1 Selection of SRT-8 digital quotients图1 SRT-8除法商数字选择图
从图1可以看出,相邻的两个选择区间存在着重叠区域(图中阴影部分),重叠区域的大小由冗余因子ρ和除数d决定。在重叠区域[Lk,Uk-1)内,部分商qj+1可以选取为k或者k-1。所以,在迭代计算中无需知道每次r*Pj的精确值,且无需进行精确模式下d(k-ρ)≤r*Pj<d(k+ρ)的比较操作。所以,重叠区间的存在简化了商数字选择函数的复杂性,只需知道部分余数r*Pj的前几位和除数d的前几位就可以选择出商数字qj+1,从而提高其运算效率。并且,重叠区间越大,比较操作中所需要的精度越小,因此,冗余度越高,商选择函数的逻辑复杂度越低。
3 总体结构设计
本文设计的SIMD浮点除法器总体结构如图2所示。
SIMD浮点除法器支持一个IEEE-754标准双精度浮点除法或两个并行单精度浮点除法,主要包括三个执行站:
E1站:数据输入及预处理。在E1级接收以IEEE-754标准表示的被除数与除数,并解析这两个输入操作数,以分离出尾数与指数;运算前调整模块整合了尾数调整与指数调整的功能,其主要作用是将操作数调整为SRT-8运算单元所要求的格式与精度。
E2站:SRT-8迭代除法计算。在E2级设计控制与计数模块,主要负责双、单精度的除法迭代计数(分别迭代18次和9次)以及异常处理与汇报。该模块实现了一个简单的状态机,是运算单元的直接管理中心。SRT-8运算单元是运算核心所在,其性能决定了整个设计的运算速度,所以本文对该模块进行了充分的优化。
E3站:规格化。在E3级后规格化模块将尾数除结果与指数减结果按IEEE-754浮点标准执行规格化操作,另外还包括例外数据判断。
所设计的SIMD主体结构是在经典低延迟64位双精度浮点除法基础上进行改进,充分利用硬件复用,包括商数字选择逻辑、余数产生57位并列加法器、尾数舍入规格化等复用逻辑,相比经典低延迟结构,面积增加较小,能实现双精度浮点除法和两个并行的单精度浮点除法。
4 优化设计策略
两个浮点数据相除,被除数与除数的符号位进行异或运算得到结果的符号位;被除数的指数减去除数的指数得到中间指数结果PreEXP;被除数与除数的尾数部分进行定点除运算,定点除法使用SRT-8除法算法。
在传统SRT-8除法迭代计算实现中,如图3所示,每一次SRT-8迭代涉及的运算有:
(1)部分余数Pj经过移位器左移三位生成8*Pj;
(2)然后以8*Pj和d为输入,经商选择逻辑查表得到该次循环的商qj+1;
(3)通过qj+1选择乘积值F=-qj+1*d;
(4)最后通过加法器运算得到下一次循环的部分余数Pj+1。
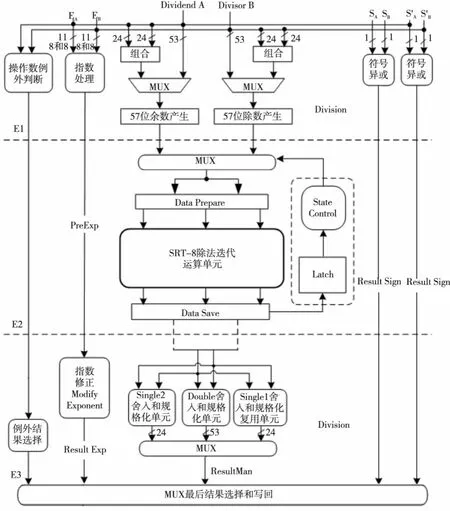
Figure 2 Overall structure of SIMD floating-point division图2 SIMD浮点除法器总体结构

Figure 3 Traditional implementation of SRT-8 division’s iteration图3 传统SRT-8除法迭代实现
4.1 商选择函数
依据上述SRT-8算法分析,商选择函数部件位于算法设计的关键路径上,该部分实现会影响到整个设计的时间延迟。在SRT-8算法中采用了冗余的商数字集,只需要知道部分余数值范围就可以决定本次商的结果。所以,只需要部分余数的前几位数值就可以得到本次循环的结果(如图4)。采用这种方法可以在降低时间延迟的同时,减少商选择函数硬件实现的复杂度。

Figure 4 Selective function of digital quotients图4 商数字选择函数
首先将除数d∈[1,2)划分成长度为2-δ的小区间[di,di+1),且d1=1/2,di+1=di+2-δ。这样,区间就用除数的前δ位小数和一位整数“1”来表示。在小区间[di,di+1)里,qj+1=k,如果mk(i)≤r Pj<mk+1(i),选择常数mk定义如下:

设选择常数mk的最小长度为2-C,则:

其中,Ak(i)为整数。

最坏情况下,k=a,d=1,可推导出:

得出δ的下界后,通过表1可以得出δ+C的最小值。

Table 1 Boundaries of r*Pj表1 r*Pj的界限(/7)
取δ=4,此时C=3,δ+C取最小值7。
4.2 SRT-8迭代单元设计
从图3可以得出,关键路径主要在于商数字选择函数查找表的延迟和57位全加器的延迟,如果这两个逻辑能够并行执行,延迟将会得到大大改观。因此,我们对以上方式进行改进,如图5虚线框所示。首先由五个加法器计算所有可能的部分余数(其中3d和5d分别分解为(d+2d)和(d+4d),并且通过进位节省加法器CSA3-2来加速运算),与此同时,以8*Pj和d为输入,经商选择逻辑查表得到该次循环的商qj+1;然后再通过qj+1选择余数Pj+1。

Figure 5 Parallel iteration of SRT-8(1)图5 SRT-8并行迭代(改进1)
通过改进1,关键路径中的商数字选择延时被虚线框内的加法器掩盖。
SRT-8迭代改进2如图6所示,对于3d和5d,事先用加法器把结果计算出来并储存,这样迭代延迟(虚线框内)将会减少一级CSA3-2压缩的时间,从而提高系统频率。
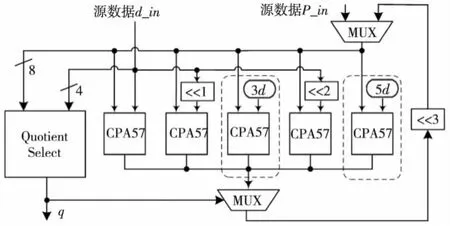
Figure 6 Parallel iteration of SRT-8(2)图6 3d和5d预先计算SRT-8并行迭代(改进2)
4.3 SIMD结构设计
SIMD数据通路结构主要由三个部分组成:数据准备(Data Prepare)、迭代计算模块和数据储存(Data Save),如图7所示。
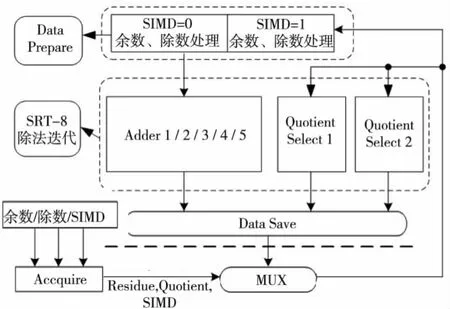
Figure 7 Structure of SIMD division’s iteration图7 SIMD除法迭代结构
数据准备模块主要负责余数和除数加减前的数据准备。当为双精度除法时,若余数符号位为0,则余数减去F,余数末位设为1(因为通过左移,余数末端三位全为0),除数求反;若余数符号位为1,则余数加上F。当为SIMD双单精度除法时,若高28位余数2符号位为0,则余数2减去F2,余数2末位设为1,28位除数2求反,否则余数2和除数2均不变;若低28位余数1符号位为0,则余数1减去F1,余数1末位设为1,28位除数1求反,否则余数1和除数1均不变。在计算SIMD双单精度除法时,余数和除数的中间位设为0。
迭代计算模块复用商数字选择部件1,求双精度尾数除法每次迭代商数字和单精度1尾数除法每次迭代商数字,增加商数字选择部件1,求单精度2尾数除法每次迭代商数字;复用57位并列加法器1/2/3/4/5,求双精度尾数除法每次迭代后的余数和两个并列单精度1、单精度2尾数除法每次迭代后的余数。
数据储存模块是每次迭代后余数和商结果的数据保存。余数的存储包括通过商qj+1来选择余数Pj+1以及余数通过移位器左移三位,以便于下次迭代运算;商的存储主要运用了商数字转换技术(详细见4.4节)。
4.4 商数字存储
由于在迭代中计算结果是用冗余数表示,需要将其转换为非冗余二进制形式。最直接的办法是将冗余数分为正数位和负数位两部分,再将其相加可得非冗余的二进制数。但是,这样做增加了控制的复杂度和迭代时间。
在SRT算法中应用商数字的存储技术,在每次迭代中将商数字分别存入两个单独的寄存器Q与QM。其中,q表示第j次迭代产生的以二进制补码形式表示的商值。每次迭代的结尾,商数字选择函数产生q后,寄存器Q与QM被刷新,如表2所示。
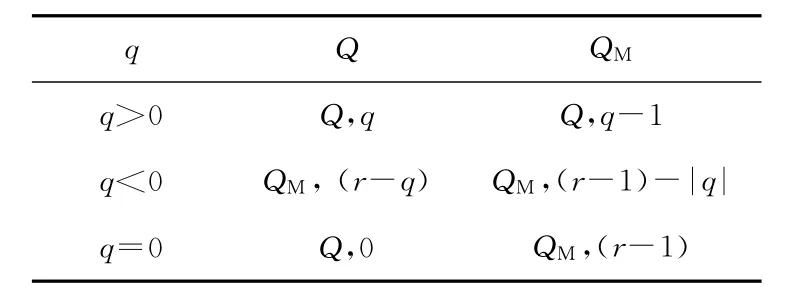
Table 2 Storage of digital quotients表2 商数字存储
可见,其中不存在算术操作,且无进位/借位的传递问题。在除法运算的最后一步迭代完成后,二进制补码形式表示的商值即保存在Q寄存器中。
5 验证与性能评估
5.1 验证流程与结果
从下列角度对SIMD浮点除法部件进行全面验证,如图8所示。
(1)功能验证完备性。主要测试RTL代码的功能正确性,验证了IEEE-754标准中的各种浮点数异常和溢出处理。异常的处理主要是除数为0、Den,无穷大除以无穷大和无效数;溢出的处理是指数上溢与指数下溢。

Figure 8 Flow chart of verification图8 验证流图
(2)数据验证完备性。采用随机数验证方法对双精度除法和两个并行单精度除法均测试了300万组随机数据,并将执行结果与对应的C黄金模型模拟作比较,结果表明实现SIMD浮点除法器的功能正确。
(3)系统验证完备性。在模拟环境下搭建好DSP内核平台,在此基础上对RTL代码进行了系统级仿真,联合其它部件在DSP内核下测试一些典型算法大程序的运行结果,与模拟器仿真硬件执行作比较,验证结果显示正确,符合设计要求。
本文对所设计的浮点除法部件进行了代码覆盖率分析。为了得到代码覆盖率,需要对源代码进行分解,分解的过程就是在源代码的关键位增加断点,记录该位置是否存在特殊结构,然后用验证平台来对这些分解的代码进行模拟,得到覆盖率信息。经过对未覆盖到的代码进行审查和增加测试激励,使代码覆盖率达到100%。
5.2 性能分析与评估
基于40 nm标准单元库在“Typical”典型常温常压(1 V,25°C)综合条件下对SIMD浮点除法器实现进行综合,逻辑优化后的综合结果如表3所示。选取时序约束时钟周期400 ps,其中设置第一站(E1)的输入延时为100 ps,以用于数据读取,第三站(E3)增加了50 ps的输出延迟,用于数据写回,两个模块在关键路径延迟设计上相对于E2站要短一些,使得各站之间延迟均匀。除法器综合运行频率可达2.5 GHz,综合cell面积为18 601.968 1μm2。

Table 3 Synthesized results of the division表3 除法器综合结果
综合优化结果与图3经典的SRT-8结构、文献[9]采用由SRT-4和SRT-2重叠组成的结构(不复用结构,实现双精度浮点除法和双单精度浮点除法)在相同工艺、相同综合条件下的综合结果比较如表4所示。面积为经典SRT-8结构的91.79%、文献[9]结构的69.57%;关键路径为经典SRT-8结构的76.19%、文献[9]结构的98.03%。性能提升来自以下技术:商选择和余数加法的并行处理技术降低了计算延时;商数字存储技术有效降低了存储商延迟。采用商选择和余数加法的并行处理技术,虽然增加了四个并行的57位全加器,但是商数字存储技术,却减少了一个57位和两个30位全加器。SIMD结构采用复用策略,如图7所示,复用商数字选择部件1,复用57位并列加法器1/2/3/4/5,有效地减少了硬件开销。

Table 4 Comparison of divisions’synthesized results表4 除法器综合结果比较
6 结束语
本文设计实现了一个支持双精度和两个单精度的SIMD浮点除法部件。本设计改进了SRT-8迭代结构,并运用商数字存储技术,加速了除法运算速度。采用了SIMD结构,能够并行计算两个单精度浮点除法。复用了硬件资源,减少了资源开销,节省了整体的面积。本文从子系统级验证完整、功能验证完全和数据验证完备的角度出发,对运算单元进行了功能验证,在验证过程中进行了代码覆盖率分析,使代码覆盖率达到100%。综合结果表明,40 nm工艺库下,综合cell面积为18 601.968 1μm2,综合运行频率可达2.5 GHz。相对传统SRT-8结构,面积减少8.21%,同时关键路径仅为传统SRT-8结构的76.19%。相对文献[9]的结构,性能提高1.97%,同时硬件面积仅为文献[9]结构的69.57%。
[1] Oberman S F,Flynn M.Design issues in division and other floating-point operations[J].IEEE Transactions on Computers,1997,46(2):154-161.
[2] Oberman S F.Floating-point division and square root algorithms and implementation in the AMD-K7 microprocessor[C]∥Proc of the 14th Symposium on Computer Arithmetic,1999:106-115.
[3] NVIDIA.Fermi:NVIDIA’s next generation CUDA compute architecture[EB/OL].[2009-10-10].http:∥www.nvidia.com/content/PDF/fermi_white_papers/NVIDIA_Fermi_Compute_Architecture_Whitepaper.pdf.
[4] Sharangpani H,Arora H.Itanium processor micro-architecture[J].IEEE Micro,2000,20(5):24-43.
[5] Wang Xian,Ni Xiao-qiang,Xing Zuo-cheng.The analysis and research of floating-point division[C]∥Proc of the Computer Project and Craftwork,2008:282-283.(in Chinese)
[6] Baliga H,Cooray N,Gamsaragan E,et al.Improvements in the Intel Core2 Penryn processor family architecture and microarchitecture[J].Intel Technology Journal,2008,12(3):179-192.
[7] Burgess N,Hinds C N.Design of the ARM VFP11 divide and square root synthesisable macrocell[C]∥Proc of the 18th IEEE Symposim on Computer Arithmetic,2007:87-96.
[8] Gerwig G,Wetter H,Schwarz E M,et al.High performance floating-point unit with 116 bit wide divider[C]∥Proc of the 16th Symposim on Computer Arithmetic,2003:87-94.
[9] Liu Hua-ping.Research on high-performance arithmetic for floating-point division and the elementary functions[D].Beijing:Institute of Computing Technology,Chinese Academy of Science,2003.(in Chinese)
[10] Liu W,Nannarelli A.Power efficient division square root unit[J].IEEE Transactions on Computers,2012,61(8):1059-1070.
[11] Harris D L,Oberman S F,Horowirtz M A.SRT division architectures and implementations[C]∥Proc of the 13th IEEE Symposium,1997:18-25.
[12] Fandrianto J.Algorithm for high-speed shared radix-4 division and radix-4 square-root[C]∥Proc of the 8th IEEE Symposium on Computer Arithmetic,1987:73-79.
[13] Wang Wen-guang.Design and implementation of double precision 64-bits floating-point division[D].Changsha:Central South University,2007.(in Chinese)
附中文参考文献:
[5] 王县,倪晓强,邢座程.浮点除法算法的分析与研究[C]∥计算机工程与工艺,2008:282-283.
[9] 刘华平.高性能浮点除法及基本函数功能部件的研究[D].北京:中国科学院计算技术研究所,2003.
[13] 王文广.双精度64位浮点除法运算单元的设计与实现[D].长沙:中南大学,2007.

