基于占用率的体系结构脆弱因子在线计算方法*
潘送军,陈传鹏
(1.国网湖南省电力公司信息通信公司,湖南长沙410007;2.中国科学院计算技术研究所,北京100190)
1 引言
随着CMOS制造工艺的不断进步,单个芯片上集成的晶体管数目增多,微处理器性能快速提升的同时,也越来越容易受到软错误的影响,软错误已成为高可靠微处理器设计时必需考虑的问题。所谓软错误,是指电路由于受到宇宙射线中高能粒子或芯片封装中α粒子的辐射作用,产生的单比特位翻转,从而改变存储数据或逻辑电路运算结果。微处理器中不同结构发生软错误的概率与芯片设计和制造工艺有直接关系,Shivakumar P等人[1]分析发现,随着工艺技术的进步,不同电路结构(如:静态随机访问存储器、锁存器、逻辑单元等)中发生软错误的概率将不断增高。
Mukherjee S S等人[2]首先提出体系结构脆弱因子AVF(Architectural Vulnerability Factor)指标,用于量化分析软错误对微处理器不同结构的影响。AVF指的是某一结构中发生的软错误,经过传播最终导致程序运行出错的概率。AVF值越高,表明该结构中发生软错误导致程序执行出错的概率越高,反之则越小。AVF计算可通过分析体系结构正确执行位ACE位(Architecturally Correct Execution bit)进行。ACE位指的是改变该比特位的值将改变程序运行结果,反之改变该比特位的值对程序运行没有影响称为非ACE位。某一结构的AVF值即为该结构包含ACE位的时间占总执行时间的比例。针对软错误,学术界已经提出了许多容错方法,如:AR-SMT[3]、DIVA[4]和SRT/SRTR[5]等,上述方法采用线程级的冗余实现对软错误的检测或恢复,没有考虑AVF值的量化指导作用,导致较大的性能、面积和功耗开销。此外,不同结构的AVF值随着应用程序以及程序运行阶段的变化而波动,可在AVF值高的时候采用严格的保护措施,而在AVF值低的时候采用轻量级的容错技术,实现微处理器可靠性与性能之间的折衷。因此,精确计算不同结构的AVF值,对于指导可靠性设计,选取合适的容错技术,具有重要意义。
本文在对已有方法分析的基础上,提出了一种基于占用率的AVF在线计算方法,并在一款周期精确的模拟器上进行验证。实验结果表明,该方法能有效计算不同结构的AVF值,与离线计算方法相比,发射队列IQ(Issue Queue)、重排序缓存ROB(Reorder Buffer)和存取队列LSQ(Load/Store Queue)AVF的平均绝对误差仅为0.10、0.01和0.039。
本文内容按如下结构组织:第2节介绍相关工作;第3节详细介绍本文提出的AVF在线计算方法;第4节介绍实验平台并给出实验结果,最后对本文进行总结。
2 相关工作
目前,学术界就AVF计算已开展了多方面的研究。AVF计算主要分为两大类:一类是离线计算,离线计算采用微处理器性能模拟器,根据应用程序的运行特征,评估不同结构中发生软错误对程序运行的影响,包括基于ACE位的计算方法[2,6,7]和基于故障注入的计算方法[8]。离线计算无需考虑对微处理器性能的影响,便于在前期阶段指导可靠性设计。另一类是在线计算,在线计算随着程序的执行,计算不同结构的AVF值,并根据计算结果动态选择容错技术,降低容错技术带来的性能开销[9,10]。例如,Walcott K R等人[9]提出一种基于线性规划的方法动态预测AVF值。该方法利用线性规划算法建立AVF值与系统性能参数之间的关系。通过运行部分样本程序得到AVF和不同性能参数之间的关系因子,并建立对应的关系等式,然后预测其它程序执行时的AVF值。由于该方法需要较长的离线分析时间,且在运行不同应用程序时需要调整参数,使得计算结果的准确性无法保证。
此外,Li X D等人[10]提出一种基于指示位的AVF在线计算方法。该方法通过在逻辑结构及存储结构上增加故障指示位表示故障的注入与传播,用于在线计算AVF值。为使计算结果具有统计意义,该方法需要注入大量故障。在故障效应表现出来之前,程序已经向前执行一段时间,使得计算结果具有滞后性,未能体现在线计算的时效性。
根据上述分析,在线AVF计算需要快速得到应用程序执行时不同结构的AVF值,要求计算方法尽量简捷,以减少对微处理器性能的影响。本文提出一种基于占用率的AVF在线计算方法,通过记录程序运行时不同结构的占用率,计算不同结构的AVF值。
3 基于占用率的AVF在线计算方法
对于离线AVF计算,由于不需要考虑ACE位分析对微处理器性能的影响,可在指令执行完成后的任意时间段内进行。而在线AVF计算是在程序实际运行过程中进行的,要求计算方法快捷,实现开销小,因而很难进行精确的ACE位和非ACE位分析。本文提出的基于占用率的在线计算方法将从另外一个角度分析计算不同微处理器结构的AVF值。
3.1 整体框图
如图1所示是本文方法的整体框图,图1中给出了一个典型的微处理器流水线结构图,包括流水线的各个阶段以及对应的结构。本文选取IQ、ROB和LSQ三个微处理器结构进行分析计算,主要是由于上述三个结构在流水线中起到非常重要的作用,IQ用于保存从译码阶段过来的指令,当指令的操作数准备好以后再将指令发射出去;ROB用于保存指令序列,以支持乱序执行和实现精确中断;LSQ用于保存存取指令。上述任意一个结构中发生软错误,导致程序执行出错的概率将非常高。
为支持本文提出的在线计算方法,需要增加相应的硬件资源。图中加阴影的部分为额外增加的硬件,主要包括指令指示位和AVF计算部件。如图1所示,IQ和ROB中每个入口项增加一位指示位,用于标识存入的指令类型;AVF计算部件,根据不同结构的使用情况,计算相应的AVF值。AVF计算部件主要包括:记录不同结构占用率的计数器;计算AVF值的运算器;临时保存计算结果的存储单元;保存AVF阈值的寄存器;此外还包括比较器、表决器等。
3.2 计算流程
在任意程序执行过程中,如果认为待分析结构中包含的比特位都为ACE位,则一段时间内该结构的占用率即为该结构AVF值的上限。假定微处理器中IQ包含32项,某一时刻该结构已使用24项,则该时刻IQ的占用率为75%,也即IQ的AVF值上界为75%。AVF值与占用率的关系可表示为:

其中,R为不同结构的占用率,λ为软错误发生的概率。由上式可知,根据占用率计算AVF值避免了记录程序执行过程中不同指令的停留时间,也不用区分指令中包含的ACE位和非ACE位,计算方法非常简捷。不足之处是,由于没有区分指令中的非ACE位,计算结果将大于实际值,进而放大了软错误对程序运行的影响。为提高计算精度,本文通过对程序运行时的指令类型进行分析,提出以区分NOP指令的方法提高计算精度。
通过运行SPEC CPU 2000基准测试程序集,根据不同指令对程序运行结果的影响可将指令分为三大类:ACE指令、动态无效指令以及NOP指令。ACE指令是指对程序运行结果有影响的指令,该类指令中包含的所有比特位都为ACE位。动态无效指令是指该指令的执行结果不会被其它指令使用,或者仅被动态无效指令使用。改变动态无效指令的执行结果对程序最终结果没有影响,也即动态无效指令中操作数指示位为非ACE位。第三类为NOP指令,NOP指令在微处理器执行过程中不进行任何操作,主要作用是取指时按字对齐或减少取指时的访存次数,也即NOP指令中只有操作码为ACE位,其余位为非ACE位。
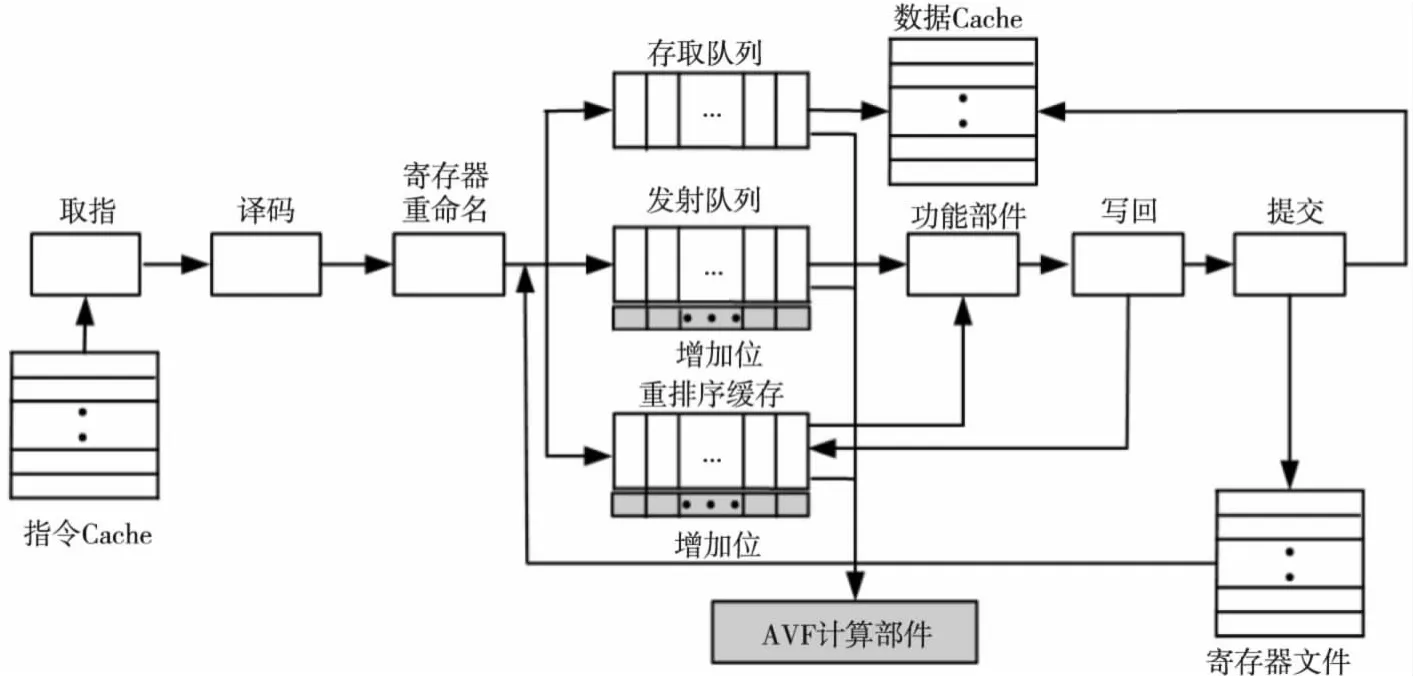
Figure 1 Framework of occupancy-based AVF computing method图1 基于占用率的在线AVF计算框图
在程序执行过程中区分ACE指令和动态无效指令,需要根据指令执行结果是否被后续指令用到来确定,分析时间将长达数百个时钟周期。对于在线计算方法,由于要快速得到程序运行时不同结构的AVF值,如果分析时间过长,一方面达不到动态选择容错技术的目的,另一方面将导致严重的性能降级。因此,本文计算方法中,将动态无效指令也视为ACE指令。图2中给出了运行SPEC CPU 2000整型测试程序时,ACE指令、动态无效指令和NOP指令所占的比例,分别为73.5%、15.8%和10.7%。由图2可知,程序执行过程中,ACE指令起主导作用,动态无效指令所占比例相对较低,且包含的非ACE位数量少,将动态无效指令视为ACE指令所引起的计算误差小。

Figure 2 Instruction types of different benchmarks图2 不同测试程序中的指令类型
本文实验中采用Alpha指令集分析NOP指令所占的比例。由图2可知,不同测试程序运行时包含的NOP指令数变化明显,从3.8%到46.4%,其中gzip中包含的NOP指令数目最多。所有程序包含的NOP指令平均值为10.7%,与Fahs B等人[11]的研究结果一致。由于NOP指令对程序运行结果没有影响,且易于区分,当计算不同结构的AVF时,排除该结构中包含的NOP指令,就能提高AVF计算精度。
为区分不同结构中存入的指令类型,本文方法是在IQ和LSQ的每个项中增加一位标识位(如图1所示)。当程序指令进入流水线中执行时,在译码阶段可判断出具体的指令类型,如果该指令为NOP指令,则相应的标识位置为1,反之置为0。最后计算占用率时,减去包含的NOP指令,即可得到更为准确的结果。采用上述方法能快速计算IQ和ROB的AVF值;而对于LSQ,由于发射到其中的指令均为存数和取数指令,仅与访存相关,不包含NOP指令,因此无需增加标识位。计算LSQ的AVF值时,可以直接将该结构的占用率作为计算结果。

Figure 3 Flowchart of our AVF computing method图3 基于占用率的AVF在线计算流程
图3给出了本文方法的计算流程,通过对指令类型进行分析,区分NOP指令后,记录不同结构的占用率,在线计算相应结构的AVF值。根据计算得到的AVF值,进一步判断该计算结果是否大于系统设定的AVF阈值,据此选择合适的容错技术来提高系统可靠性。此外,在系统开销方面,本文方法的计算过程与指令执行是并行的,AVF计算过程本身对性能没有影响。由于在实现过程中增加了部分硬件结构,如指示位、AVF计算部件等,本文方法的开销主要为面积开销,相对于现代数以亿计晶体管的微处理器,上述增加的面积开销可以忽略不计。
4 实验平台和实验结果
4.1 实验平台
本文所有实验都基于Sim-Alpha模拟器[12]开展,该模拟器为商用微处理器Alpha 21264对应的性能模拟器。为了支持在线计算不同结构的AVF值,本文对Sim-Alpha模拟器进行了修改。主要包括分析程序运行过程中的指令类型、统计不同结构占用率、实现AVF计算算法等。由于Sim-Alpha模拟器不能精确模拟浮点测试程序,因此本文后续实验中,仅选用SPEC CPU 2000基准程序中的12个整型程序进行分析,每个程序编译成Alpha指令格式的二进制指令。为减少程序执行时间,本文利用Sim-Point[13]工具选取测试程序的一部分指令代替整个程序,实验中每个测试程序运行50M条指令,使用的输入为参考输入集。Sim-Alpha模拟器的初始配置参数如表1所示。本文计算IQ、ROB和LSQ三个结构的AVF值,对应的项数分别为20、80和64。
4.2 计算时间间隔选取
在线AVF计算是在程序执行过程中连续计算AVF值,其中的关键步骤是选取合适的计算时间间隔,也即每隔多长时间计算一次AVF值。计算时间间隔最大可为程序的整个执行时间,最小可为单个微处理器时钟周期,上述两种情形为时间间隔的极端选择。选取的时间间隔过短,则会频繁计算AVF值,不仅会使微处理器增加额外的功耗开销,同时计算结果也将随着程序特征的变化而快速变化,不利于指导容错技术的选择。Soundararajan N等人[14]分析了AVF值按单个时钟周期的变化特征,由于计算时间间隔仅为一个时钟周期,程序运行过程中的不确定因素主导着AVF值,很难验证计算结果的准确性。相反,如果选取的时间间隔过长,计算过程中将会丢失程序运行的一些细节特征,同样难以保证计算的准确性。

Table 1 Simulated microprocessor configuration表1 模拟的微处理器配置参数
为了选定合适的时间间隔,本文选取三个不同大小的时间间隔进行分析,分别是200个时钟周期、1 000个时钟周期和5 000个时钟周期。如图4所示为运行crafty测试程序时,不同时间间隔下AVF值的变化特征。由图4可知,当时间间隔设为200个时钟周期时,由于运行过程中不确定因素的影响,计算得到的AVF值变化非常显著。当时间间隔设为1 000个时钟周期时,计算结果能够较好地反映程序运行特征,同时没有随着程序的变化而发生剧烈的波动;而当时间间隔设为5 000个时钟周期时,计算结果的变化趋势变小,很难反映程序不同阶段的运行特点。因此,在本文后续实验中,选用的计算时间间隔为1 000个时钟周期。在每个时间间隔的末尾,AVF计算部件将得出该时间间隔内不同结构的AVF值,同时初始化相应的计数单元,为下一时间段的AVF计算做准备。
4.3 实验结果及分析
本节利用提出的AVF在线计算方法计算IQ、ROB和LSQ三个结构的AVF值,给出计算结果并进行分析。

Figure 4 AVF varies for different program intervals图4 以crafty测试程序为例,时间间隔分别为200、1 000及5 000个周期时AVF值的变化特征
如图5所示为运行不同测试程序时,本文在线方法与离线方法[7]计算IQ、ROB和LSQ三个结构的AVF值。由图5可知,与离线计算方法得到的结果相比,上述三个结构的AVF值的绝对误差分别为0.10、0.01和0.039,说明采用本文方法计算AVF值的准确度较高。同时,实验结果与前述分析均表明,本文提出的在线方法计算结果偏大,即AVF值具有一定的保守性,造成上述偏差的原因是本文方法没有足够时间区分动态无效指令,将其全部视为ACE指令。

Figure 5 Results of our method compared with an offline method图5 本文方法与离线方法AVF计算结果
此外,ROB和LSQ AVF值的平均偏差比IQ AVF值的平均偏差小,这是由于ROB与LSQ的项数比IQ的项数多,ROB和LSQ的占用率相对于IQ的占用率小,因此计算AVF时,动态无效指令对ROB和LSQ的影响比对IQ的影响小。实验中的一个特例是在运行gzip测试程序时,本文方法得到的ROB AVF值比离线计算结果要小,这是因为运行gzip测试程序时,其中有45.6%的指令是NOP指令,本文方法中该部分指令没有加以计算,但NOP指令中的操作码为ACE位,离线计算中进行了分析,使得运行gzip测试程序时,离线计算结果比在线计算结果更加精确。
图6给出了本文方法与离线计算方法比较的相对误差。对于IQ和ROB,通过区分NOP指令提高了计算精度,因此平均相对误差较小,分别为24%和5%。而对于LSQ,由于该结构AVF的绝对值偏小,较小的计算误差将导致很大的相对误差,比如运行twolf时,相对误差达到72%。虽然对LSQ结构有较大的相对误差,但该结构的AVF绝对值较低,也即该结构中发生软错误被屏蔽的概率非常高,产生的计算误差对容错设计的影响相应减小。

Figure 6 Relative error of our method to an offline method图6 本文方法和离线方法比较的相对误差
图7给出了运行crafty和gap时,IQ、ROB和LSQ三个结构的AVF值,选取的计算时间间隔为1 000个时钟周期。由图6可知,当运行crafty测试程序时,三个结构的AVF值在一个较大范围内波动。而IQ AVF值比其它两个结构的AVF值要高,上述结果与本文前述分析一致。当运行测试程序gap时,AVF值的变化范围相对较小,可见程序运行过程中,不同结构的AVF值将随程序特征的变化而变化。
实验结果表明,本文提出的AVF在线计算方法能快速计算微处理器中不同结构的AVF值,对选择容错技术、提高微处理器可靠性具有较好的指导作用。当AVF值较高时,可采用严格的冗余技术提高系统可靠性,例如采用程序完全冗余执行技术。而当AVF值较低时,即便发生软错误,程序执行出错的概率也较小,此时可采用开销较小的容错技术降低对性能的影响,例如采用程序部分冗余执行技术。通过适时调整容错策略,就能在微处理器性能、功耗和可靠性等方面进行折衷,达到最优配置。

Figure 7 IQ,ROB and LSQ AVF during executing crafty and gap图7 运行测试程序crafty和gap时,IQ、ROB和LSQ三个结构的AVF值,计算时间间隔为1 000个时钟周期
5 结束语
CMOS工艺技术的不断进步使得软错误成为影响微处理器可靠性的重要因素,量化分析软错误对微处理器中不同结构的影响对提高微处理器可靠性具有重要指导意义。本文在对已有AVF计算方法分析比较的基础上,提出了一种基于占用率的AVF在线计算方法,该方法通过在程序运行过程中记录不同结构的占用率、分析指令类型并排除NOP指令来计算不同结构(IQ、ROB和LSQ)的AVF值。实验结果表明,该方法能有效计算微处理器中不同结构的AVF值,与精确的离线计算方法相比,IQ AVF、ROB AVF和LSQ AVF的平均绝对误差仅为0.10、0.01和0.039。后续工作是将本文方法与具体的容错技术相结合(例如,双线程冗余技术),在程序运行过程中,动态选择不同的容错技术,在可靠性与性能之间实现较好的平衡。
[1] Shivakumar P,Kistler M,Keckler S,et al.Modeling the effect of technology trends on the soft error rate of combinatorial logic[C]∥Proc of the International Symposium of Dependable Systems and Networks(DSN’02),2002:389-398.
[2] Mukherjee S S,Weaver C,Emer J,et al.A systematic methodology to compute the architectural vulnerability factors for a high performance microprocessor[C]∥Proc of the International Symposium on Microarchitecture(MICRO’03),2003:29-40.
[3] Rotenberg E.AR-SMT:A microarchitectural approach to fault tolerance in microprocessors[C]∥Proc of the Fault-Tolerant Computing Systems(FTCS’99),1999:84-91.
[4] Austin T.DIVA:A reliable substrate for deep submicron microarchitecture[C]∥Proc of the International Symposium on Microarchitecture(MICRO’99),1999:196-207.
[5] Vijaykumar T,Pomeranz I,Cheng K.Transient-fault recovery using simultaneous multithreading[C]∥Proc of the International Symposium on Computer Architecture(ISCA’02),2002:87-98.
[6] Pan Song-jun,Hu Yu,Li Xiao-wei.IVF:Characterizing the vulnerability of microprocessor structures to intermittent faults[J].IEEE Transactions on Very Large Scale Integration(VLSI)Systems,2012,20(5):777-790.
[7] Fu X,Li T,Fortes J.Sim-SODA:A unified framework for architectural level software reliability analysis[C]∥Proc of Workshop on Modeling,Benchmarking and Simulation,2006:1.
[8] Saggese G P,Wang N,Kalbarczyk Z,et al.An experimental study of soft errors in microprocessors[J].IEEE Micro,2005,25(6):30-39.
[9] Walcott K R,Humphreys G,Gurumurthi S.Dynamic prediction of architectural vulnerability from microarchitectural state[C]∥Proc of the International Conference of Computer Architecture(ISCA’07),2007:516-527.
[10] Li X D,Adve S V,Bose P,et al.Online estimation of architectural vulnerability factor for soft errors[C]∥Proc of the International Conference of Computer Architecture(ISCA’08),2008:341-352.
[11] Fahs B,Bose S,Crum M,et al.Performance characterization of a hardware mechanism for dynamic optimization[C]∥Proc of the International Symposium on Microarchitecture(MICRO’01),2001:16-27.
[12] Desikan R,Burger D,Keckler S,et al.Sim-alpha:A validated,execution-driven Alpha 21264 simulator[R].Technical Report TR-01-23,Austin:Department of Computer Sciences,University of Texas at Austin,2001.
[13] Sherwood T,Perelman E,Hamerly G,et al.Automatically characterizing large scale program behavior[C]∥Proc of the International Conference on Architectural Support for Programming Languages and Operating Systems(ASPLOS’02),2002:45-57.
[14] Soundararajan N,Parashar A,Sivasubramaniam A.Mechanisms for bounding vulnerabilities of processor structures[C]∥Proc of the International Symposium on Computer Architecture(ISCA’07),2007:506-515.

