融雪径流模型在嫩江流域的应用

薛 梅，冯 艳，孙启伟

（水利部松辽委水利委员会，吉林 长春 130021）

融雪径流模型在嫩江流域的应用

薛 梅，冯 艳，孙启伟

（水利部松辽委水利委员会，吉林 长春 130021）

文章以数字高程模型（DEM）和地理信息系统（GIS）为基本支撑，将尼尔基流域划分为 12个子流域，基于子流域构建分散式融雪径流模型，通过模拟各个子流域出口的融雪径流，并结合各子流域之间的空间拓扑关系和汇流计算，实现尼尔基水库的融雪径流预报。应用结果表明，该模型在一定程度上达到了模拟预报尼尔基水库入库水量的目的。

融雪径流;度日因子法;径流系数法;新安江

1 引 言

融雪水资源是中高纬度地区重要的淡水资源之一，在工农业生产和城镇生活用水中扮演着重要的角色。然而，积雪融化过程中有可能产生洪水，有时还会对社会经济造成严重的损失和破坏。因此，加强对春季融雪径流的研究，掌握融雪原理，模拟融雪过程，做好对春季融雪径流的预测预报，对于当地防洪抗旱、合理开发水资源，促进国民经济可持续发展，都具有十分重要的意义。

2 分散式融雪径流模型

分散式融雪径流模型主要由度日因子法结合径流系数法及三水源新安江模型构成，分散式融雪径流模型进行径流计算主要包括4部分：根据DEM 划分的子流域及各个子流域划分的计算单元[1-4]，以前期积雪的雪水当量控制，采用度日法计算融雪期内的融雪水量，将计算所得的融雪水量及降雨量作为模型的基本水文资料输入，并对每个计算单元进行产流计算；融雪期内径流计算，采用径流 系 数法[5-7]进 行 子 流域汇流计算，得 到子流域出口断面径流过程；融雪期结束后径流计算，采用三水源新安江模型进行子流域汇流计算，其中子单元汇流采用线性水库，子单元河网汇流采用马斯京根法演算至各子流域出口断面；全部子流域出口流量通过马斯京根法进行河网汇流演算至尼尔基流域出口，得到尼尔基流域融雪径流过程。

2.1 度日法加径流系数法

2.2.1 降水输入

模型的输入是一个或若干个测站的实测降水，模型要根据测站实测降水估算各计算单元的降水。一般情况下用插值的方法，但地形对降水的影响比较明显，需要进一步作地形修正。

设置 两个 临界 气温 阈值（Tsnow、Train）作 为 判断 降水形态的依据[8]。当日平 均 气温 T 在 Train以上时，所有降水为液态降雨；当日平均气温在 Tsnow以下时，降水类型为固态降雪；当日平均气温在两个临界气温之间，则按比例进行分配，如式（1）所示：

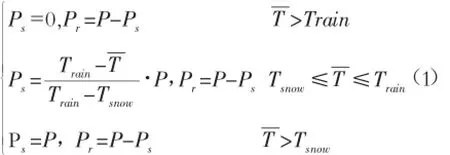
式中，P，Ps，Pr分别为日降水量、雪水当量及降雨量，单位为 mm。

这样第 n 日计算单元内积雪的雪水当量 Sn为：

2.2.2 融雪计算

在实际计算中，每日融雪水总量需以前期累积积雪的雪水当量控制。如果流域前期累积积雪的雪水当量小于可能总融雪量M时，则积雪全部融化，第n日实际融雪水量等于前期累积积雪的雪水当量，即，其中 m=1，…，n 表示日积雪过程序列。

2.2.3 径流量计算

在各个子流域，第 n+1 日融雪径流量（包括降雨径流量）Qn+1采用下式计算 （以模拟日径流量为例，假设该子流域根据泰森多边形划分为3个计算单元 A、B、C）：

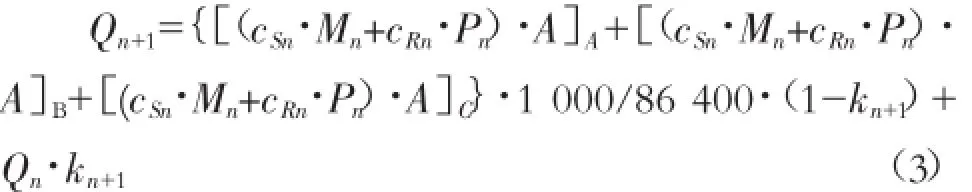
式中：Q 为流域面平均日径流量，m3/s；c 为径流系数；cS表示融雪径流系数；cR表示降雨径流系数；Pr为降雨量，mm；A 为计算单元面积，km2；k 为退水系数，表示在没有融雪或降雨的时段内流量的下降值。

2.2.4 河网汇流计算

河网汇流计算采用在我国被广泛应用的马斯京根法[9]。计算公式如下：，I1，O1，为时段初的入流和出流；I2，O2为时段末的入流和出流；K 为槽蓄曲线的坡度；x 为流量比重系数；△t为时段长。

2.2 三水源新安江模型

新安江模型是由原华东水利学院赵人俊教授等提出，并在近代山坡水文学的基础上改进成为现在的三水源新安江模型[10-12]。新安江模型是分散型结构，根据 DEM 划分的子流域及各个子流域划分的计算单元，先对每个计算单元作产汇流计算，得出计算单元的出口流量过程，采用马斯京根法将其演算至子流域出口断面。子流域出口断面以下河网汇流采用分段马斯京根法进行计算，最终将所有子流域汇流结果进行累加，得到尼尔基流域出口断面流量过程。

单元面积水文模拟采用：

1）蒸散发计算。新安江模型中，采用三层蒸散发模型计算蒸散发量。参数有流域平均张力水容量WM，上层张力水容量UM，下层张力水容量LM，深层张力水容量 DM，蒸发折算系数 KC，深层蒸散发扩散系数C。

2）产流计算。采用蓄满产流理论，即包气带土壤含水量达到田间持水量之前不产流，此前的降水与融雪全部被土壤吸收，补充了包气带缺水量，待包气带蓄满后，所有降水与融雪都产流。考虑到包气带蓄水容量在流域上分布的不均匀性，模型中采用了蓄水容量曲线，曲线用B次方抛物线来表示。主要参数有流域包气带平均张力水蓄水容量 WM，流域不透水面积所占的比例 IM，蓄水容量～面积分配曲线的指数。

3）分水源计算。模型将总径流量划分为三水源，即地 面径流（RS）、壤中 流（RSS）和地下 径流（RG）。模型中引入自由水蓄水容量曲线表示自由水蓄水容量在产流面积上分布的不均匀性。主要参数有自由水蓄水容量曲线方次 EX，自由水蓄水容量 SM，壤中流出流系数 KI，地下水出游系数 KG。

4）汇流计算。流域汇流包括地表径流汇流，采用单位线或线性水库计算；壤中流汇流采用线性水库或滞后演算法计算；地下径流汇流采用线性水库计算；单元面积河网汇流采用滞后演算法；单元面积以下河道汇流皆采用马斯京根法。

3 模型应用与结果分析

3.1 子流域划分

传统的融雪径流预报模型由于缺乏山区降水、气温与积雪分布规律资料，且模型并不能很好考虑地形及下垫面对产汇流的影响，融雪径流预报效果差。文中基于 DEM 数据，将尼尔基流域划分为 12个子流域。

3.2 模型应用

经过对尼尔基流域历年资料的分析，假定每年 4 月 10 日至 5 月 10 日为融雪期；5 月之后积雪全部融化，但积雪产生的径流并没有完全退完，加之冬季产生的冻土层完全解冻大致在每年8月中旬，因此将计算时段延长至 8 月 31 日，从而进行水文预报模型的参数率定及验证。

为排除基础输入资料对水文模型预报精度的影响，选择尼尔基流域资料齐全的年份参与模型的参数率定及验证。根据资料收集情况，尼尔基流域12 个子流域率定期 1979 年至 1988 年（4 月 10 日-8 月 31 日），验证期为 2001 年至 2003 年 （4 月 10日-8 月 31 日）。

3.3 结果分析

1979—1988 年，模型计算所得径流水量与同时段实测径流水量相对误差小于等于 20%的旬比例为 85%，春汛期比例为 60%，率定时段的比例为100%。2000-2003 年相对误差在 40%以内旬比例、春汛期比例、率定时段比例分别为 23%、25%，25%。尼尔基流域出口断面率定期及验证期统计结果见表1。

表1 尼尔基流域出口断面率定期及验证期统计结果表

结果表明：尼尔基流域率定期率定结果较好，模型在一定程度上达到了模拟预报尼尔基水库入库水量的目的；验证期统计结果明显次于率定期统计结果，这主要是以下两个原因造成的：

1）资料误差。验证期尼尔基流域内资料齐全的站点个数相较于率定期有所减少，将导致对各子流域基础水文资料预处理存在一定误差，输入资料的误差进而影响最终计算结果的精度。

2）模型概化误差。研究区域水文气象复杂，不考虑融雪水夜间重新封冻和冻土冻融等影响的水文预报模型只是对该流域实际水文循环的一种概化，预报结果必然会存在一定的误差。

4 结论

文中以数字高程模型（DEM）和地理信息系统（GIS）为基本支撑，将尼尔基流域划分为 12 个子流域，基于子流域建分散式融雪径流模型，通过模拟各个子流域出口的融雪径流，并结合各子流域之间的空间拓扑关系和汇流计算，实现尼尔基水库的融雪径流预报。

1）模型在一定程度上达到了模拟预报尼尔基水库入库水量的目的，为实现尼尔基水库融雪径流预报、水资源管理及防洪兴利调度提供决策支持，同时，也填补了嫩江流域在融雪径流预报方面的空白。

2）分散式融雪径流模型采用度日因子法、径流系数法计算融雪与积雪，耦合三水源新安江模型。模型考虑了降雨和积雪的差异与共性，是一种适合融雪径流计算和降雨径流计算的水文模型，模型具有先进性。

3）基于 DEM、GIS 将尼尔基流域划分为 12 个子流域，基于子流域构建分散式融雪径流模型，充分考虑空间分布不均匀性，具有“分布式”设计思想。

4）尼尔基水库控制流域站点相对稀疏，难以反映水文要素空间分布不均匀性，影响了径流模拟的精度。但随着尼尔基水库的运行，实测资料的累积，理论上模型精度将有所改善，并为尼尔基水库的兴利调度提供依据。

［1］张珂，郭毅，李致家等.基于 DEM 的流域信息提取方法及 应 用 实例田［J］.水 力发电 ，2005 ，31（2）：18-21.

［2］张柯.基于 DEM 栅格和地形的分布式水文模型构建及其应用［D］.南京：河海大学，2005.

［3］俞鑫颖，刘新仁.分布式冰雪融水雨水混合水文模型［J］.河海大学学报（自然科学版），2002，30（5）:23-27.

［4］李舟.寒区流域分布式水资源模拟模型研究及应用［D］.南京：河海大学，2008.

［5］穆振侠，石启中，姜卉芳.基于 RS 和 GIS 的融雪型新安江模型参数的确定［J］.人民黄河，2009，31（1）：38-40.

［6］景少波，姜卉芳，穆振侠.含融雪结构的新安江模型在叶尔羌河流域的应用［J］.新疆农业大学学报，2010，33（3）：250-254.

［7］李利琴.黄河河源区径流模拟及变化分析［D］.南京：河海大学，2007.

［8］李利琴.新安江与融雪径流的混合模型在黄河源区的应用［C］.第三届黄河国际论坛论文集，2007：328-233.

［9］包为民.水文预报［M］.北京：中国水利水电出版社，2006.

［10］王佩兰.三水源新安江模型的应用经验［J］.水文，1982，5：26-33.

［11］赵人俊.流域水文模型—新安江模型和陕北模型［M］.北京：水利电力出版社，1984.

［12］芮孝芳，水文学原理［M］.北京：水利水电出版社，2004.

TV212+.6

B

1002－0624（2014）11－0033－03

2014-05-29