基于偏振分束器的保偏型光纤传感器解调方法

张淑芳，张锦龙，毛海涛，2，周德让

(1．河南大学物理与电子学院，河南开封　475004；2．河南大学民生学院，河南开封　475004)

0　引言

加拿大渥太华通信研究中心的KHILL K O等人于1978年首次在掺锗石英光纤中发现光纤的光敏效应，并采用驻波写入法制成世界上第一只光纤光栅[1-3]。它首先被用做传感器，是目前最优良的传感器之一，具有很多其他传感器不具备的优点，如高反射、选频和色散等特性，使之立刻被用在光纤通信和激光光源中。光纤光栅传感器是一种典型的波长调制型光纤传感器，它具有抗干扰能力强、结构简单、精确性高、可用于外界参量的绝对测量、便于规模生产等优点，但也存在不足之处，例如，对波长移位的检测需要用较复杂的技术和较昂贵的仪器或光纤器件，需要大功率的宽带光源或可调谐光源，检测范围和分辨率也受到一定限制等。目前，制约光纤光栅传感器实用化的关键技术是对传感信号的精密解调[4-6]。因此，人们对光纤光栅的解调技术进行了深入的研究，先后提出了许多解调方法，其中干涉法解调法以高分辨率的独特优势成为研究的重点，但干涉解调法的解调精度受环境的影响太大[7-10]。文中依据线偏振光干涉和PBS分光原理提出了一种新型波长解调方案。研究保偏光纤长度、主轴与偏振方向夹角对PBS两臂输出光强与入射光波长关系的影响，设计了基于PMF和PBS的干涉型解调系统，并对几种参数的测试结果进行了比较分析。结果显示该解调仪不仅结构简单，而且稳定性良好、检测精度高，与理论分析一致。

1　结构设计及原理分析

图1为文中设计的传感器解调系统示意图，由光源发出线偏振宽光谱通过耦合器(optical fiber coupler，OFC)进入光栅，符合Bragg反射条件的窄带光被反射，从OFC左边的另一端口进入。线偏振光Ein由A点射入长度为L1的PMF，由于Ein偏振方向与PMF应力主轴的方向不相同，在此段保偏光纤中激起两个正交的偏振模式。两种模式传送到B点经一段普通的单模光纤后进入偏振分(合)束器，两种模式又会激起4个正交的偏振模式同时产生干涉现象，最后由偏振分束器两输出臂输出光场E1、E2。偏振分束器的主轴方向和PMF输入光场偏振方向如图1中的虚线框内部分所示，α为A点Ein偏振方向与L1主轴的夹角，β为B点PMF主轴与偏振分束器主轴的夹角。

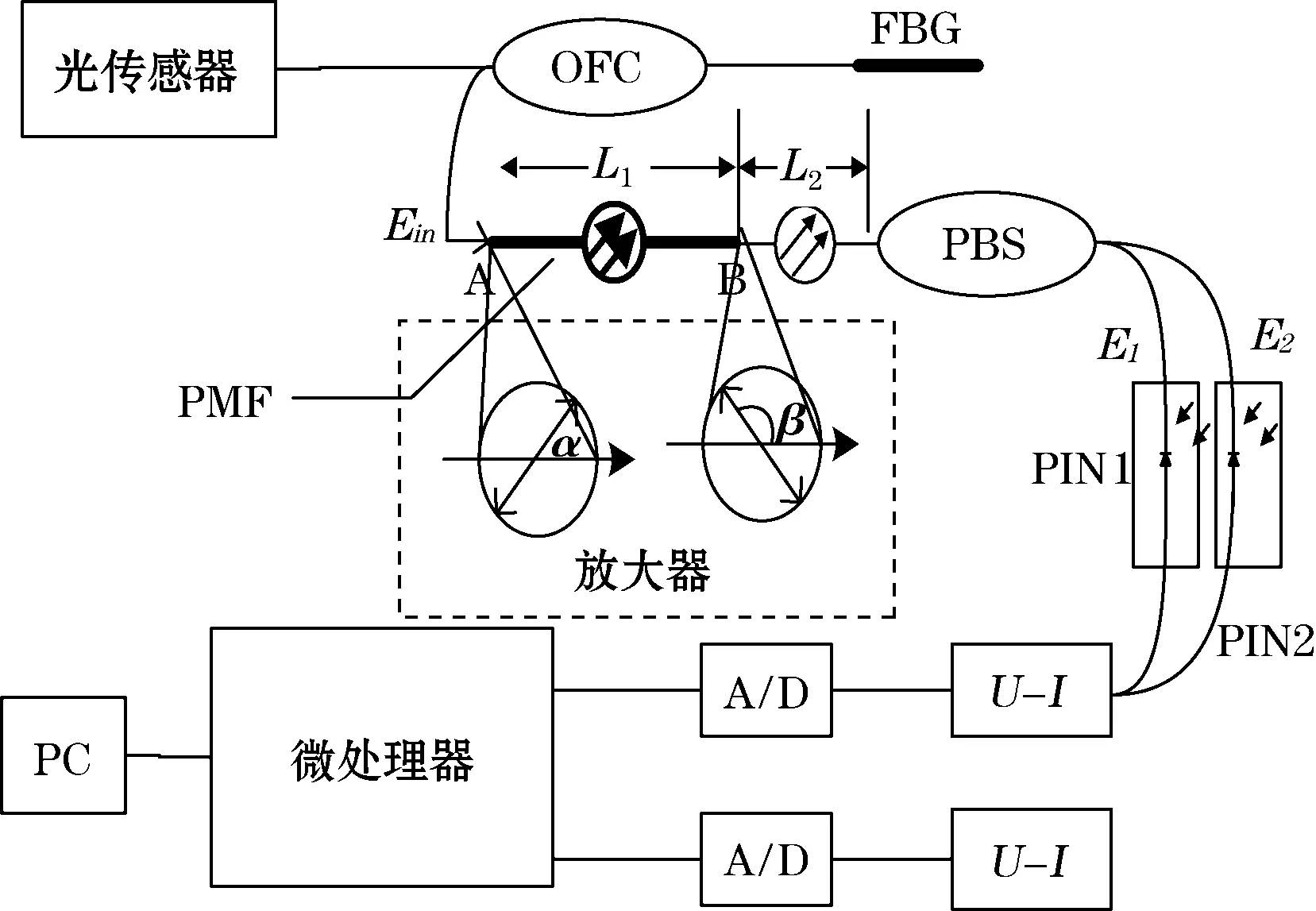
图1　系统结构图

在理论分析中，不计光纤传输过程中的损耗，依据矩阵光学原理[11]该光路的传输矩阵为：

Eout=Tout·TSM·Tβ·TS·TS·Ta·Tin·Tin

(1)

式中：Eout为输出光光场；Tin给出了光场在A点的相位；Ein为入射光场，

(2)

Tα、Tβ分别是A、B两点旋光器的传输矩阵，

(3)

用δx、δy分别表示PMF快、慢轴的相位延迟，则可PMF传输矩阵可表示为：

(4)

式(5)为模光纤传输矩阵：

(5)

式中：k为波矢；η为光纤损耗系数；l为光纤长度。

由于单模光纤是PBS的输入尾纤且长度L2很小，则光场在B点与PBS之间传输过程中偏振态不变，故这段长度为L2的单模光纤的影响可以忽略，所以PBS的输出矩阵可写为：

(6)

联立以上各式，可得：

Eout=

(7)

E1、E2和Eout满足：

(8)

由光功率公式p=(其中< >为时间上求平均)得E1、E2对应的光功率分别为

P1=cosα2·cosβ2+sinα2·sinβ2-

2sinα·sinβ·cosα·cosβ·cos(δx-δy)

P2=cosα2·sinβ2+sinα2·cosβ2+

2sinα·sinβ·cosα·cosβ·cos(δx-δy)

(9)

光场在PMF快慢轴上的相位差：

δ=|δx-δy|=2πBmL1/λ

式中：Bm为PMF的双折射度；L1为PMF长度；λ为入射光的波长。

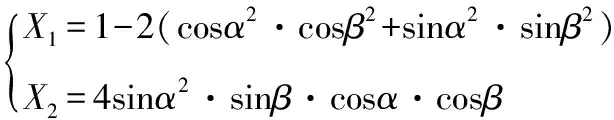
(10)

带入式(9)得：

(11)

令

(12)

由式(12)知，η是PMF长度L1、两偏振方向的夹角α、β和波长λ的函数。α、β和L1为系统结构参数值，只要系统确定，它们则为定值，X1、X2也为常数，且分别可看作直流分量和交流分量的最大值。波长λ随温度t线性变化，它们的关系可表示为：

λ=λ0+Ct，

式中：λ0为0℃时的波长；C为FBG的温度系数[12]。

由此可知，η和t也具有一一对应的函数关系，所以测出η就可求得温度值t。因此该解调方案可应用于光纤光栅传感系统。如图1所示，利用PIN1和PIN2两个探测器将PBS探测到的光强P1和P2转化为电流，再经I-U转换器等效为电压，后经A/D转换器将模拟信号转化成数字信号。由单片机进行数据采集和处理后传送给PC，最后利用Matlab7．0接收数据，并依据理论模型计算出η值，从而可得到对应的温度值。

2　系统仿真

因光纤光栅反射波长λ与温度t一一对应，故要研究η和t的关系，可直接研究η和λ的关系。根据式(12)通过Matlab7．0进行数值计算研究参数L1、α、β对η和λ对应关系的影响。

图2是α=2π/3、β=π/3、L1由0～2 m变化时η随λ变化的曲线：

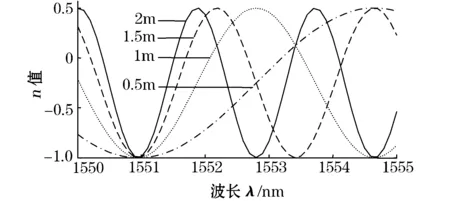
图2　L1变化时η和λ关系图

由图2可知：L1增大，η随λ的变化灵敏度增高；而η的直流分量X1、交流分量最大值X2均不随L1的变化而变化，故PMF应尽量长以使检测灵的敏度更高。但同时还可以看出η随λ的变化曲线具有周期性，周期随L1值增大而变短，传感系统检测时只能取一个单调区间，故PMF长度的选择应根据实际检测的温度范围而定。

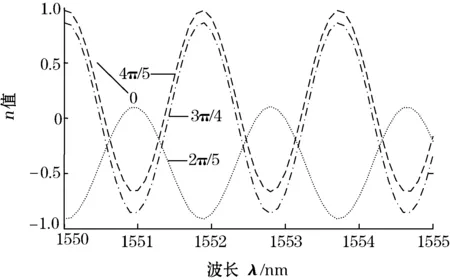
图3　α变化时η和波长λ关系图

图3为L1=3 m、β=π/3、α从0～π变化时，η和λ的函数曲线。由图3可知：η随波长λ变化周期不随α的变化而变化；α越趋近π/4(3π/4)X2越大，η随λ变化的灵敏度也越高；α接近0(π/2、π)时η几乎不变，η随波长λ变化的灵敏度为0，即波长变化无法被检测。因此，在传感系统中应使得α尽可能趋近π/4(3π/4)。由式(10)知β和α是对称关系，所以β也尽可能趋近3π/4或π/4。

分析以上仿真结果知，针对需要的测量范围，选取合适的结构参数搭建系统可提高测量精度。该系统虽然也基于偏振干涉的原理，但相比于M-Z干涉解调法，稳定性更好，且比其他传感系统有更高的测量精度。

3　实验结果与分析

基于以上理论模型，搭建了测试系统验证光路结构各参数对光纤光栅传感系统精度的影响。在试验系统中，调谐精度0.001 nm、带宽0.01 nm的可调谐激光器模拟Bragg反射波长的变化；PBS两输出端口的串扰为64 dB；PMF长度2 m，拍长小于4 mm；A/D转换精度为16位；PIN管灵敏度0.85 A/W；探测、数据采集及处理和PC通信模块均是自己设计。通过光谱分析仪同步对比检测，最小分辨率0.02 nm．系统选取3m长PMF构建测试系统，在1 550～1 560 nm范围内用可调谐的激光器进行扫描，用R和T分别表示E1对应的反射能量和E2对应的透射能量，R(T)和λ关系如图4所示。

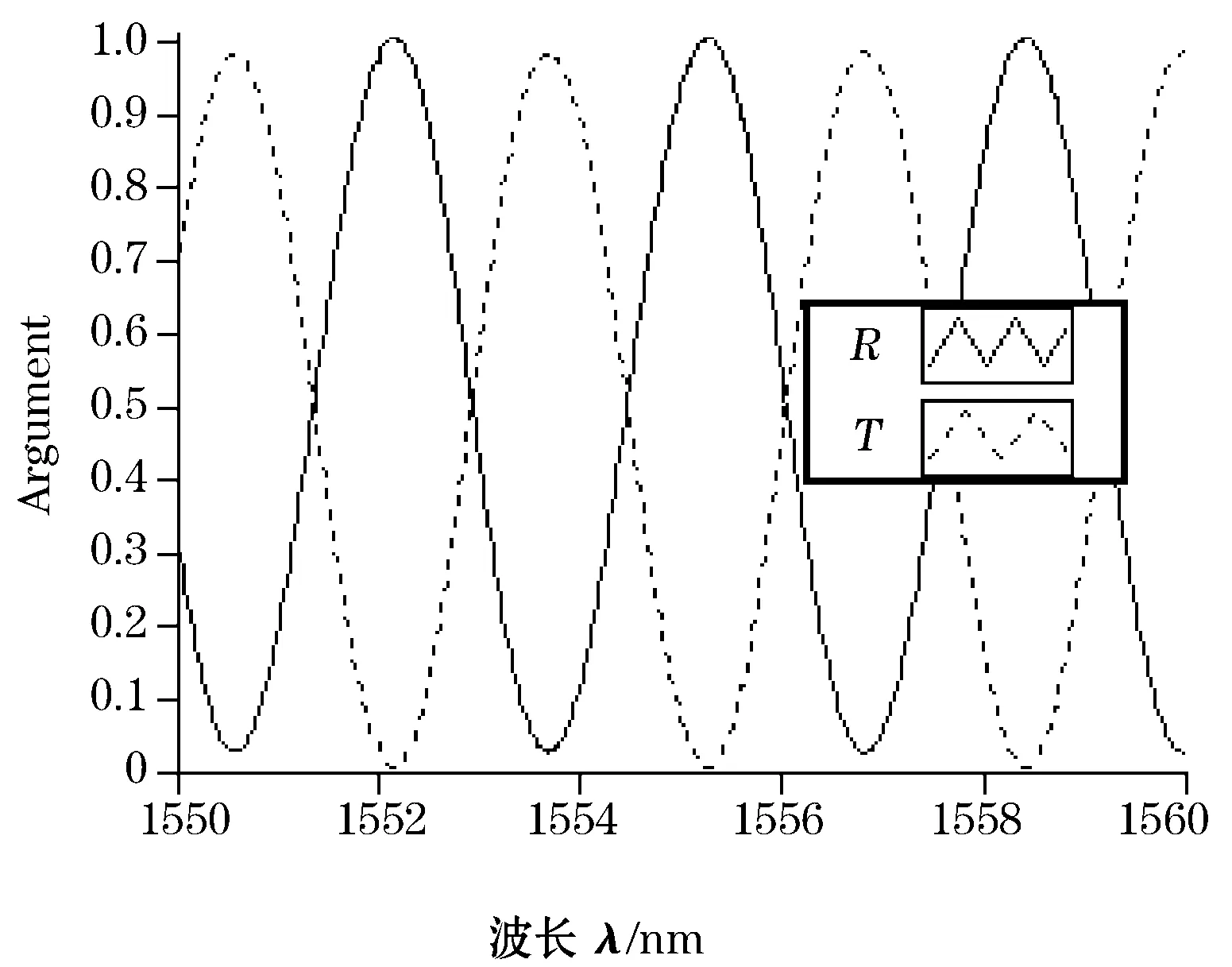
(a)

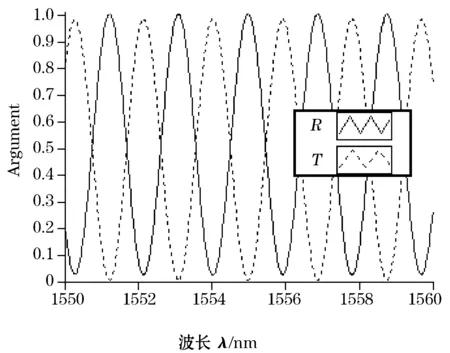
(b)

所得实验结果与数值仿真结果一致。实验值和理论值间的偏差主要是由PMF长度的测量误差、OFC制作的分光比误差、偏振方向的控制误差造成的。

普通光纤光栅中心波长温度系数0.01 nm/℃[8]，依据以上结果，选用L=1.2 m、α=λ/4、β=3π/4的系统，可测量范围超过1 nm(即温度测量范围超过100℃)。该参数组成的系统最大测量范围为1.5 nm；理论上此系统输入信号的功率达-10 d Bm时，分辨率是0.055 pm，其由A/D转换的位数决定。光谱仪和可调激光器分辨率最高为1 pm，测量结果因此只能精确至pm量级，所以该系统针对波长的分辨率小于1 pm，故测量的精度在±1 pm之间。该方案的稳定性虽得到了提高，但环境温度的影响并没有彻底避免，温度对PMF双折射度的影响在数量级10-3，明显低于其它解调系统。

4　结束语

基于PBS的保偏型光纤传感器的解调是一种独特创新的方法。文中探讨了系统各结构参数对输出光场的影响，建立理论模型进行数值仿真，搭建传感解调系统进行试验测试，结果均与理论分析相吻合，且系统的测量精度在±1 pm之间，分辨率低于1 pm．由此，在实际应用中可调节PMF长度、挑选耦合系数适当的OFC和调整PMF主轴角度来提高系统的分辨率并得到理想的测量范围。相比于其它解调方法，该系统不仅有很好的稳定性和独立性，而且采用全光纤搭建，易于实现小型化，对光纤光栅传感器的应用具有重要意义。

参考文献：

[1]张军，李成刚，姚莉君．压电式六维加速度传感器实时信号处理系统．仪表技术与传感器，2012(11)：4-5．

[2]高迎慧，刘宾，王佳，等．基于DSP和FPGA的高速数据采集处理系统．仪表技术与传感器，2011(2)：66-68．

[3]HILL K O，FUJI Y，JOHNSO官D C，et al．Photo-sensitivity in optical fiber waveguides：Application to reflection filters fabrication．Physics，etters．1978，32：647-649．

[4]董大圣，程群，陈世哲，等．原位叶绿素a和浊度传感器设计．仪表技术与传感器，2012(10)：19-20．

[5]何元，张会新，刘波．基于FPGA的高速实时数据采集存储系统设计．仪表技术与传感器，2011(8)：64-67．

[6]姚东伟，王培先，张江波．便携式倾角传感器的研究设计．仪表技术与传感器，2012(11)：25-27．

[7]裴峰，张志杰，王文廉，等．传感器补偿系统中的小波去噪的应用及DSP的实现．仪表技术与传感器，2012(12)：89-91．

[8]张锦龙，余重秀，王葵如，等．基于偏振干涉的光纤光栅传感解调方法分析．物理学报，2009，58(6)：3989-3990．

[9]李建中，饶云江，冉曾令．基于可调环形光纤激光器的动态应变传感系统．光电子．激光，2008，19(2)：146-148．

[10]张锦龙，余重秀，王葵如，等．基于啁啾光纤光栅的温度自补偿位移传感器．光学学报，2008，28(4)：779-781．

[11]张智，杨道业，程明宵．双阵列式电容传感器的特性研究和参数优化．仪表技术与传感器，2012(12)：17-20．

[12]于秀娟，余有龙，张敏，等．铜片封装光纤光栅传感器的应变和温度传感特性研究．光子学报，2006，35(9)：1325-1327．