一种基于稀疏表示的DOA估计新方法

张天恒，季华益，曾德国

（中国航天科工集团8511研究所，江苏南京210007）

0 引言

对辐射源进行精确的测向定位是现代战争中的重要作战环节之一，因此，波达方向（DOA）估计理论和算法的研究具有极大的军事应用价值［1］。实际的测向装备面临的是一个很宽的频段，同时空间中本身包含着诸如线性调频、扩频等宽带信号，如何对这些信号的DOA进行高精度的估计是一个巨大的挑战。目前经典的DOA估计方法是基于阵列的空间谱估计法。以MUSIC为代表的信号子空间算法使测向定位技术突破了分辨率的限制，但该算法有计算量大、在低信噪比条件下性能不佳等缺点，且该算法不能直接对相干信号进行处理，而利用空间平滑的方法解相干则会损失一定的阵列孔径［2］。

与经典的谱估计法相比，基于稀疏表示的DOA估计法具有很高的估计精度，无需任何预处理，并可直接应用于相干信号，因而得到了国内外学者的广泛关注。Malioutov等［3］提出了利用频率和角度构建联合字典的方法。但该方法随着频段的展宽，字典的长度随之增加。这一方面增加了计算量和存储量；另一方面，在宽频段范围内很难保证字典内没有相同的元素，当存在相近的元素时，字典的相干性不能满足，稀疏分解的精度急剧下降。

针对以上问题，本文引入空间频率的概念，提出了一种基于空间频率的DOA估计方法。该方法的字典在整个带宽内恒定不变。利用阵列接收信号的频域数据建立稀疏模型，可以同时对带宽范围内的多个窄带和宽带信号进行高精度DOA估计。

1 数学模型

1.1 阵列数据DOA估计数学模型

假设K个远场信号入射到阵元间距为d的M个均匀线阵上。第i（i＝1，2，…，K）个信号的方位角为θi，频率为fi。M个阵元接收到的数据可以表示为一个矢量：

式中，A（f，θ）是M×K维阵列流形矩阵，S（t）＝［sf1，θ1（t），sf2，θ2（t），…，sfK，θK（t）］T为K×1维空间信号矩阵，噪声矩阵N（t）是与信号无关的M×1维高斯白噪声。阵列流形矩阵为：

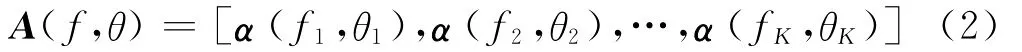
其中第i个导向矢量为：

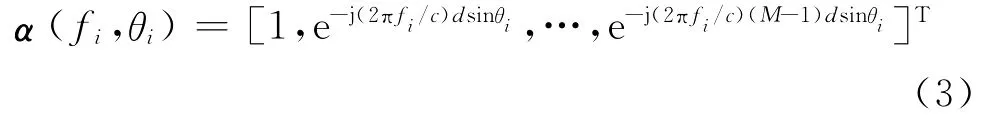
式中，c为电磁波传播速度。

宽带DOA估计算法大都由窄带算法发展而来。现有的基于信号子空间的宽带DOA估计方法主要分为两类：非相干子空间法（ISM）和相干子空间法（CSM）。ISM［4］将整个宽带频段划分为若干个窄带子频段，根据每个子频段的中心频率分别建立方向矢量，这大大增加了存储空间和计算量；CSM［5］则需要构造聚焦矩阵，将不同频率的信号子空间映射到同一个参考频率上，然后将所有频率成分的信号功率谱密度矩阵做平均。该方法需要对角度进行预估计，当预估值与真实值相差较大时算法性能较差。这两类算法都需要对空间谱峰值进行搜索，且不能直接用于相干信号，而利用空间平滑的方法解相干则会损失阵列孔径。

1.2 基于稀疏表示的DOA估计模型

由于空间辐射源的个数相对于整个角度空间来说是有限的，因此辐射源在角度空间的分布具有稀疏性［6］。Mallat和Zhang首次提出了基于过完备原子库的信号表示［7］，利用其进行DOA估计的主要思想是将信号的阵列流形矩阵扩展成一个过完备的字典Φ，它包含了辐射源所有可能的角度。令θ＝｛θ1，θ2，…，θN｝，N为整个角度空间划分的网格数，则阵列流形矩阵A可以扩展成如下形式：

从Φ中找到具有最佳线性组合的m项原子来表示原信号，由于m≪N，因此该过程称为信号的稀疏表示。

定义N×1维矢量h＝［h1，h2，…，hN］，当且仅当信号源位于θn时，hn不等于零。于是DOA估计的稀疏模型为：

利用匹配追踪（MP）或基追踪［8］（BP）等稀疏分解算法求得h，再根据h中非零元素的位置即可得到信号的DOA。在进行宽带DOA估计时，Malioutov提出将宽带范围内的若干频点分别建立字典，再将若干个字典组合成一个大字典的方法，即：

式中，Nf为宽带信号频点个数。当角度空间划分为N个网格时，Ψ为M×（Nf×N）维矩阵，随着频段的展宽，稀疏分解的计算量成指数倍增长。若fisinθi＝fjsinθj，则字典中α（fi，θi）＝α（fj，θj），此时字典的相关度为1，算法的性能急剧下降。

2 基于空间频率稀疏表示的宽带DOA估计

2.1 空间频率模型的建立

为解决宽带信号字典随带宽展宽而变大的问题，令γi＝fidsinθi／c，i＝1，2，…，N，则：

为了保证无模糊测向，要求阵元间距小于波长的一半，即γ的取值范围是－0.5≤γ≤0.5。根据空间频率的取值范围划分N个网格，则过完备字典可表示为：通过求解式（5）即可得到辐射源的空间频率。

由于空间频率是频率和角度的二维函数，因此必须在频率已知时才能求出DOA。对矩阵X和S做快速傅里叶变换后的结果分别为X（f）和S（f），则有：

考察矩阵X（f）中的任一行，假设在频点fi处有峰值，则取出各通道在该频点处对应的频域值组成列向量Y，构造稀疏表达式：

通过求出向量h中非零值所在的位置，即可得到频率为fi的所有信号的DOA。

2.2 基于稀疏表示的空间频率DOA估计方法

宽带接收机所接收到的一帧数据中可能包含多个频率的信号（包括窄带和宽带）。如果将整个带宽划分为若干子频带，再分别对每个子频带进行处理，则会对没有信号的子频段进行处理，浪费计算资源。本文提出的方法根据信号在频域内的分布特点，自适应地进行信号分离，然后在有信号的频点处进行DOA估计。方法如下：

1）对阵列接收到的数据进行傅立叶变换得到信号的频域谱。任意选取一个阵列单元的频域谱进行谱峰搜索，记录下峰值及其对应的频点fi。

2）取出所有阵列单元在频点fi处的值组成一个列向量Y，按2.1节中的方法构造空间频率矩阵Φ，得到模型Y＝Φh。

3）对上式进行稀疏分解，得到频率为fi处的空间频率γ＝［γ1，γ2，…，γK］，K为信号个数。则信号的DOA为：

重复以上步骤，即可得到宽频段内所有窄带信号的DOA。

对于有一定带宽的信号，假设根据频谱判断其带宽为B，将带宽分为P段，每一段的中心频率为fp，p＝1，2，…，P。按照上面的方法构建稀疏模型，得到每个子频段的DOA估计值（fp）。对所有的估计值求平均，即得到宽带信号的DOA的最终结果

2.3 稀疏表达式的求解

求解式（10）的本质是从M个方程中求解出N个未知量（M≪N），从表面上看，这是个无法直接求解的欠定方程，然而文献［9］指出，由于信号矢量h是稀疏的，若矩阵Φ满足有限等距准则（RIP）等稀疏重构条件，则该信号时可以以很高的概率被重构出来。Candès等证明［10］，信号重构问题可以通过求解以下最小l0范数问题加以解决。

最小l0范数是一个NP难题，而文献［11］指出，采用l1范数代替l0范数可以得到如下凸优化问题：

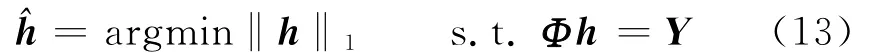
文献［12］证明了在满足一定条件时式（12）和式（13）的等价性，因此，信号重构问题可以转换为一个线性规划问题加以求解。如果考虑存在噪声的情况，上述问题可以转化为如下最小l1范数问题：

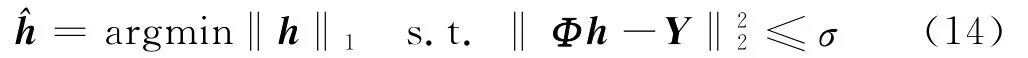
式中，σ是与噪声能量有关的参数。

本文采用基于梯度投影的BP算法求解最小l1范数优化问题来重构稀疏信号。得到稀疏信号后，进而根据非零元素的位置求得信源DOA的估计值。

3 算法仿真

3.1 空间频率法与直接恢复法和传统MUSIC法的比较

考虑6阵元均匀线阵，假设远场入射信号入射角为－30.3°，频率800MHz，采样率1GHz，阵元间距为波长的一半，时域快拍数K＝200，对时域数据做1024点FFT得到频域快拍。文献［1］采用的直接恢复法取所有的200个时域快拍构建稀疏表达式，空间域范围－90°～90°，网格划分为1801个，以多测量矢量法（MMV）求解；空间频率法的空间频率范围－0.5～0.5，网格划分为1001个，取信号频率所在的频点构建稀疏表达式，以单测量矢量法（SMV）求解。以为步长，考察信噪比为0～20dB时两种算法的性能，每个信噪比做500次蒙特卡洛实验。仿真结果如图1所示。

图1 均方根误差随信噪比变化

可以看到，空间频率法的估计误差与传统的MUSIC法相当，但远优于直接恢复法；直接恢复法所要求解的稀疏矩阵是1801×200维的（该矩阵的每一列都有相同的稀疏结构），相比而言空间频率法求解的稀疏矩阵则为1001×1维，且无需MUSIC法的空间谱峰搜索，因而空间频率法比另两种算法计算量更小。

3.2 相干信号DOA估计

假设有两个远场相干窄带入射信号，其入射角度分别－20.6°和7.8°，频率为800MHz。其它条件如前所述。SNR＝10dB，分别采用MUSIC法、空间平滑MUSIC法和空间频率法估计DOA。仿真如图2所示。

图2 相干信号DOA估计结果

对相干信号而言，传统的MUSIC算法已经基本失效，空间频率法与空间平滑MUSIC法均能对目标角度进行正确估计。为比较空间平滑MUSIC法和本文算法的估计精度，以1dB为步长，考察信噪比为0～20dB时两种算法的性能，其它条件不变，每个信噪比做500次蒙特卡洛实验。仿真结果如图3所示。

图3 相干信号估计均方根误差随信噪比变化

在低信噪比情况下，本文算法的估计精度要优于平滑MUSIC法，在SNR＞10dB时两种算法性能相当。

3.3 宽带相干信号DOA估计

假设两个宽带相干LFM信号，中心频率750MHz，带宽100MHz，入射角分别为－22.8°和6.2°。ISM法和空间频率法将带宽分为5段，在每一段都求出一个估计值，将它们的平均值作为最终结果；CSM法构造聚焦矩阵时参考频率选为750MHz，角度预估值为－5°。SNR＝0～20dB，步长1dB，每个信噪比处做500次蒙特卡洛实验。均方根误差随信噪比的变化如图4所示。

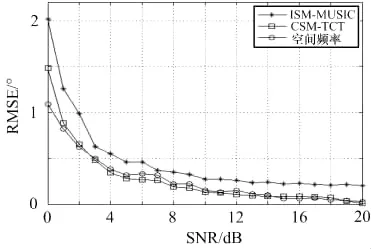
图4 均方根误差随信噪比变化

由图4可以看出，本文方法的均方根误差与CSM法相当但小于ISM法，在信噪比大于5dB的情况下，均方根误差小于0.5°。由于CSM法需要预估角度，而预估角的选择对最终的估计结果有较大影响，因此综合来看，本文提出的空间频率法较优。

4 结束语

适合宽带接收机的高精度、高分辨率宽带DOA估计算法具有重要的理论研究价值和军事应用前景。本文提出了一种基于空间频率系数分解的宽带DOA估计方法。仿真实验表明，该方法对宽频带内的多个窄带和宽带信号、相干和非相干信号的DOA进行准确估计，其精度、对噪声的鲁棒性均优于传统的MUSIC法，且明显降低了计算量，是一种适应性很强的超分辨算法。■

［1］ 林波.基于压缩感知的辐射源DOA估计［D］.长沙：国防科学技术大学，2010.

［2］ 张小飞，汪飞，徐大专.阵列信号处理的理论和应用［M］.北京：国防工业出版社，2010.

［3］ Malioutov D，Cetin M，Willsky AS.A sparse signal reconstruction perspective for source localization with sensor arrays［J］.IEEE Transactions on Signal Processing，2005，53（8）：3010－3022.

［4］ Wang Y，Leus G.Direction estimation using compressive sampling array processing［C］.15th IEEE Workshop on Statistical Signal Processing，2009：626－629.

［5］ Wang H，Kaveh M.Coherent signal－subspace processing for the detection and estimation of angles of multiple wideband sources［J］.IEEE Transactions Acoustics，Speech，and Signal Processing，1985，33（4）：823－831.

［6］ Cotter SF，Rao BD，Engan K，et al.Sparse solutions to linear inverse problems with multiple measurement vectors［J］.IEEE Transactions on Signal Processing，2005，53（7）：2477－2488.

［7］ Mallat S，Zhang Z.Matching pursuits with time－frequency dictionaries［J］.IEEE Transactions Signal Process，1993，41（12）：3397－3415.

［8］ Chen HB，Donoho DL，Saunders MA.Atomic decom－position by basis pursuit［J］.SIAM Joumal on Scientific Compting，2001，20（1）：33－66.

［9］ Donoho DL.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）：1289－1306.

［10］Candès E.Compressive sampling.In：Proceedings of International Congress of Mathematicians［M］.Madrid，Spain：European Mathematical Society Publishing House，2006：1433－1452.

［11］Candès E，Romberg J，Tao T.Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52（2）：489－509.

［12］Donoho DL，Elad M，Temlyakov VN.Stable recovery of sparse overcomplete representations in the presence of noise［J］.IEEE Transactions on Information Theory，2006，52（1）：6－18.