基于匹配追踪算法的波达方向估计方法＊

郑生华，李景峰

（中国电子科技集团第三十八研究所，安徽合肥230088）

0 引言

在雷达、声纳、通信和电子战等领域中，确定接收信号的DOA参数具有重要意义。DOA估计的波束形成法将阵列输出加权求和，使阵列天线方向图主瓣指向所需方向上，对期望信号得到最大输出功率的方向为信号源的DOA估计值。在波束形成器中，Bartlett波束形成器基于经典Fourier分析对传感器阵列数据进行延时相加处理，使波束形成器的输出功率对于某个入射信号为最大。和周期谱图谱估计类似，其分辨率低。为了克服这个缺点，Capon最小方差法使用一部分自由度在期望观测方向形成一个波束，同时利用剩余的自由度在干扰信号方向形成零陷来提高Bartlett波束形成器的性能。

波束形成器分辨率受限于瑞利限，而天线的波束宽度与阵列的孔径密切相关，为了获得超过瑞利限的更高DOA分辨率，可采用基于子空间的超分辨算法。其中，典型代表是Schmidt提出的多重信号分类（MUSIC）算法［1］和Roy等人提出的借助旋转不变技术估计信号参数（ESPRIT）算法及其修正算法［2－3］。这些算法是把线性空间概念引入到参数估计中，属于特征结构的子空间方法。其中，MUSIC算法通过构建所谓的MUSIC空间谱，根据其谱峰所对应的角度来确定DOA。由文献［1］的分析可知，只要数据长度足够长或信噪比足够高，且信号模型准确，MUSIC算法就可得到任意精度的DOA估计值。但在低信噪比和小样本情况下，分辨率损失较大，尤其对于高度相关信号更是如此。ESPRIT算法采用对称子阵的特殊阵列结构，根据子阵输出协方差矩阵之间的旋转不变性估计信号参数。基于特征子空间的DOA估计算法，为了准确获得信号子空间，需具有空间信号源数目的先验知识，或通过估计来确定信号源的数目。通过对以上常用DOA估计算法的研究和最大似然算法［4－5］思想的启发，本文提出了基于匹配追踪原理的多辐射源DOA估计新算法。该算法的主要优点有：低信噪比下增强的分辨率；不需要信源数的先验信息；不受不同方向到达信号相干性的影响且算法直接给出DOA估计值及其对应的幅度等。

1 Hilbert空间上的MP算法

匹配跟踪算法［6］（MP）是Mallat和Zhang提出的一种信号稀疏表示的基于迭代的贪心算法。算法将任意信号分解为一个从冗余字典中选择函数波形的线性展开，选择这些函数波形使其与信号结构最匹配，从而在一个冗余波形集上展开函数。

设H为一Hilbert空间，D＝（gγ）γ∈Γ，‖gγ‖＝1为此空间的过完备字典。对于字典D，如果其中的原子能够张成N维欧式空间RN，则D称为完备字典，而当原子的数目Γ＞N时，字典D是冗余的，如果还能张成N维欧式空间RN，则称此时的字典是过完备的。令f∈H，在D中选择的一个矢量集上，计算f的一个线性展开，使其与信号的内部结构最匹配，这可通过f在D中元素上的正交投影逐次逼近得到。

令gγ0∈D，则f可分解为：

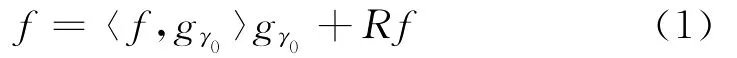
式中，Rf是分解后的余量，显然，f在gγ0方向上分解逼近后，gγ0与Rf正交，因此下式成立：

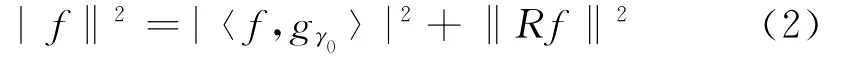
为了最小化‖Rf‖，应该选择gγ0∈D使｜〈f，gγ0〉｜最大化，即可找到一个gγ0在如下意义上是最佳的：

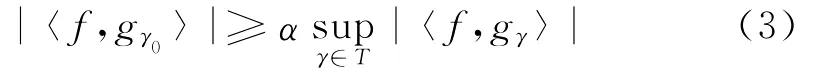
式中，α是优化因子，0＜α≤1。

MP算法通过迭代将Rf再次分解，将其投影到D中一个矢量上，使其与Rf最佳匹配，这个过程重复进行，然后得到下一个余量。

令R0f＝f，假设已经计算出的第n次分解后的余量为Rnf，n≥0，按照上述步骤选择一个元素gγ0∈D与余量Rnf匹配，使其满足：

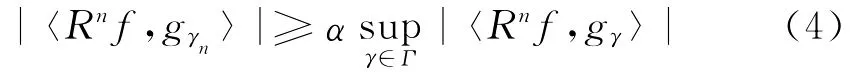
Rnf再次分解的表示式为：

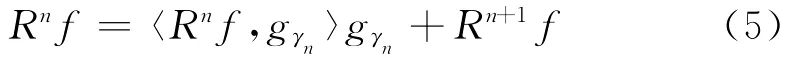
显然，n＋1阶余量Rn＋1f与gγn正交。

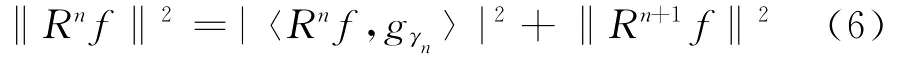
经过m次迭代分解，信号f就被分解为：

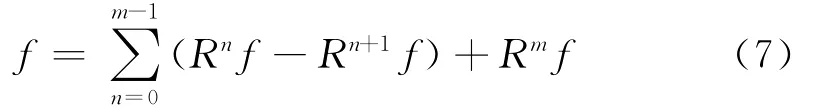
进一步可表示为：

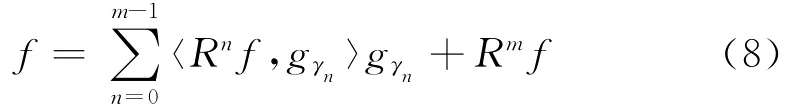
同样，‖f‖2可表示为：

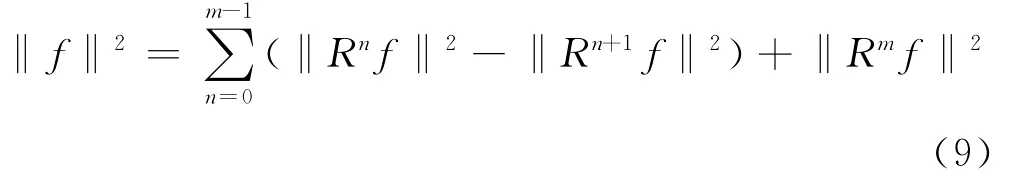
由式（6）得到能量守恒方程：

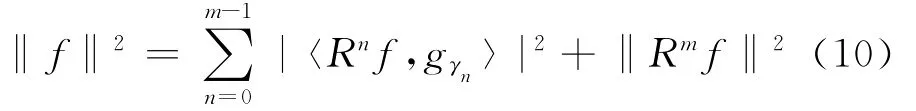
通过选择字典元素，使其不断与分解余量最佳匹配，在第m步时满足迭代终止准则，则信号f被分解为字典元素的一个和，这种分解是非线性的，则通过式（8）的和式恢复信号，逼近误差为Rmf。

2 基于匹配追踪的DOA估计

在DOA估计中，一般只有少数方向上包含入射到阵面上的信号。因此，DOA估计问题的解是稀疏的［7－8］。MP算法是信号稀疏分解的一种有效算法。MP算法应用于DOA估计时，算法通过确定一个来自大冗余矢量集的小的矢量子集来选择信号分解的一个基，将其匹配给定阵列数据矢量。这个矢量集通过天线阵元的可能输出建模，选择这些阵元的正确的线性组合问题就等效选择准确的DOA。

考虑N单元天线阵。这些阵的输出是一个N×1的矢量x。通常x对应来自不同方向信号的线性组合。如果考虑x的第i和第j单元，则xi和xj包含不同相移的相同信号，且依赖于入射信号的DOA和它们之间的距离。DOA估计问题就是从观测数据x分辨每一入射信号的DOA。

基于匹配追踪算法DOA估计的系统模型如图1所示，天线接收的信号经接收机放大、滤波和下变频之后再进行数字化，输入匹配追踪算法模块的为数字阵列数据，字典中存储用于MP算法分解的信号原子。

假设入射信号波前为平面波。接收信号矢量为x，对于等距线性阵列（ULA），字典D为：

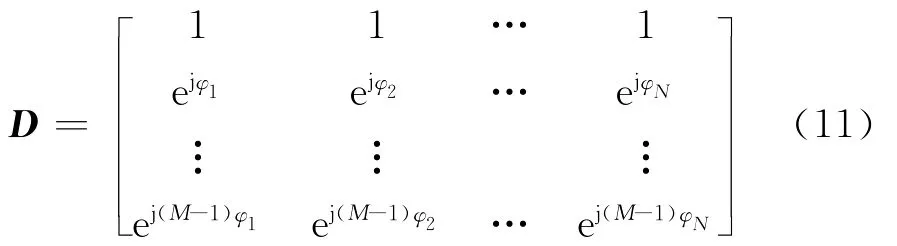
式中，φi为信号来自θi的阵元间的相位差，φi＝2πd／λcos（θi），λ为波长，d为阵元间距。

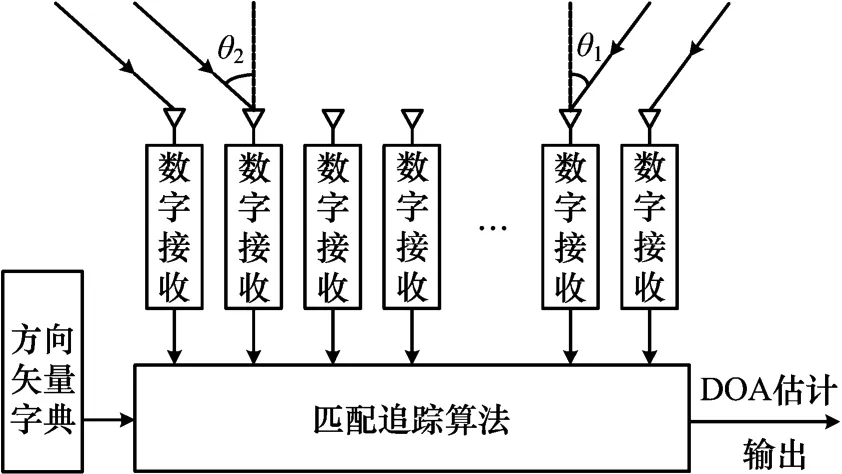
图1 基于匹配追踪算法DOA估计的系统模型

对于（1）式中的DOA，其可能范围分为N部分，形成DOA估计问题的原子，这些原子构成字典D。大小为M×1的接收信号矢量是字典D的列和噪声的线性组合，依赖于入射信号的DOA。因此，DOA估计问题就转化为寻找D的列的正确线性组合的问题。

当信号只来自一个独立的角度时，问题很直接，基于匹配追踪算法选择D的列使其与接收信号矢量x的内积最大，达到最佳匹配。然而当信号来自更多方向时，x是D的列线性组合，尝试每一可能的线性组合将给出问题的最大似然解。匹配追踪算法的原子选择具有很大的灵活性，可根据先验信息或预定的分辨率和扇形区域确定字典中的原子。MP算法通过选择字典D的列构成分解阵列接收矢量x的原子，这些列原子就对应于所需估计的信号DOA，同时算法还返回这些列原子的系数，系数对应DOA估计的幅度。

3 仿真实验和分析

为了验证所提方法的有效性，进行下列计算机模拟实验。仿真中采用16阵元的等距线阵，阵元间距为半波长。

对于辐射源为线性调频波形，分别仿真了单个辐射源（入射角为10°）和三个辐射源（入射角为10°、35°和65°）情况。图2给出了单个辐射源的信号波形和到达角分布图。从图2可以看出：对于单个LFM辐射源，MP算法在入射信号角度处形成一个尖锐的峰值，准确给出入射信号的DOA估计。

图3给出了三个辐射源的到达角分布图。从图3可以看出：对于三个LFM辐射源，MP算法在三个入射信号角度处形成尖锐的峰值，准确给出入射信号的DOA估计，同时图中也出现了估计的误差余量，但误差余量相对于信号DOA非常小，对DOA估计结果的影响几乎可以忽略不计。

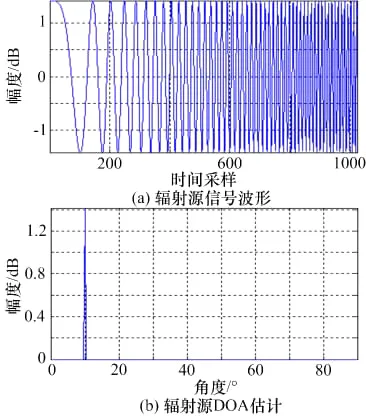
图2 单个LFM辐射源的到达角分布图

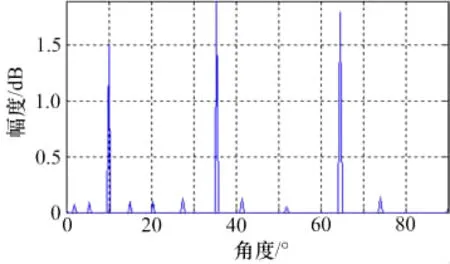
图3 三个LFM辐射源的到达角分布图

4 结束语

本文的分析仿真表明，基于匹配追踪的DOA估计算法具有比常用波束形成和子空间类算法优越的性能，该算法可以同时给出辐射源的DOA和其对应的幅度输出，算法不要求入射辐射源数目的先验知识，无需预处理，另外算法不受来自不同辐射源信号的相关性的影响，这一点在多径情况下具有实用价值，而且算法在低信噪比和小快拍数的情况下仍具有较好的到达角分辨特性。■

［1］ Schmidt RO.Multiple emitter location and signal parameter estimation［J］.IEEE Trans.on Antennas and Propagation，1986，34：176－280.

［2］ Roy R，Kailath T.ESPRIT－estimation of signal parameters via rotational invariance techniques［J］.IEEE Trans.on Acoust.，Speech，Signal Processing，1989，37：984－995.

［3］ Roy R，Paulraj A，Kailath T.ESPRIT－A subspace rotation approach to estimation of parameters of cisoids in noise［J］.IEEE Trans.ASSP，1986，34（5）：1340－1342.

［4］ Stoica P，Sharman K.Maximum likelihood methods for direction－of－arrival estimation［J］.IEEE Trans.on A－coustics，Speech，Signal Processing，38（7）：1132－1143，1990.

［5］ Stoica P，Nehorai A.MUSIC，maximum likelihood，and Cramer－Rao bound［J］.IEEE Trans.on Acoustics，Speech，Signal Processing，37（5）：720－741，1989.

［6］ Mallat S，Zhang Z.Matching pursuits with time－frequency dictionaries［J］.IEEE Trans.on Signal Processing，1993，41（12）：3397－3415.

［7］ Karabulut GZ，Kurt T，Yongacoglu A.Estimation of directions of arrival by matching pursuit（EDAMP）［J］.EURASIP Journal on Wireless Communications and Networking，2005，2：197－205.

［8］ Cotter SF.A two stage matching pursuit based algorithm for DOA estimation in fast time－varying environments［C］∥Wales，UK：Proceedings of 15thIntl.Conf.on Digital Signal Processing，2007：63－66.