群时延测量的约束条件*

周　峰　买　望　牟　丹　成　锴 胡耀峰　许　伟　徐雨绸　郭隆庆

(1.工业和信息化部电信研究院，北京 100191；2.北京邮电大学，北京 100876)

0　引言

群时延是指群信号通过线性系统或网络传播时，系统对信号整体产生的时延，是微波器件和系统的重要指标之一。一般使用矢量网络分析仪测量群时延，限于矢量网络分析仪的测量机理，在群时延较大时，往往遇到测量曲线异常的问题，本文通过理论推导和实验验证，解决了这种测量曲线异常问题。

1　问题的提出

在测量实验中，我们使用R&S AMU200A基带衰落模拟器设置一个群时延值，然后使用Agilent E5061B 矢量网络分析仪来测量该群时延值。

首先设置第一组参数：群时延202μs，矢量网络分析仪中频带宽IF=1kHz，扫频带宽1～4MHz，扫频点数1601。则测量结果如图1所示。

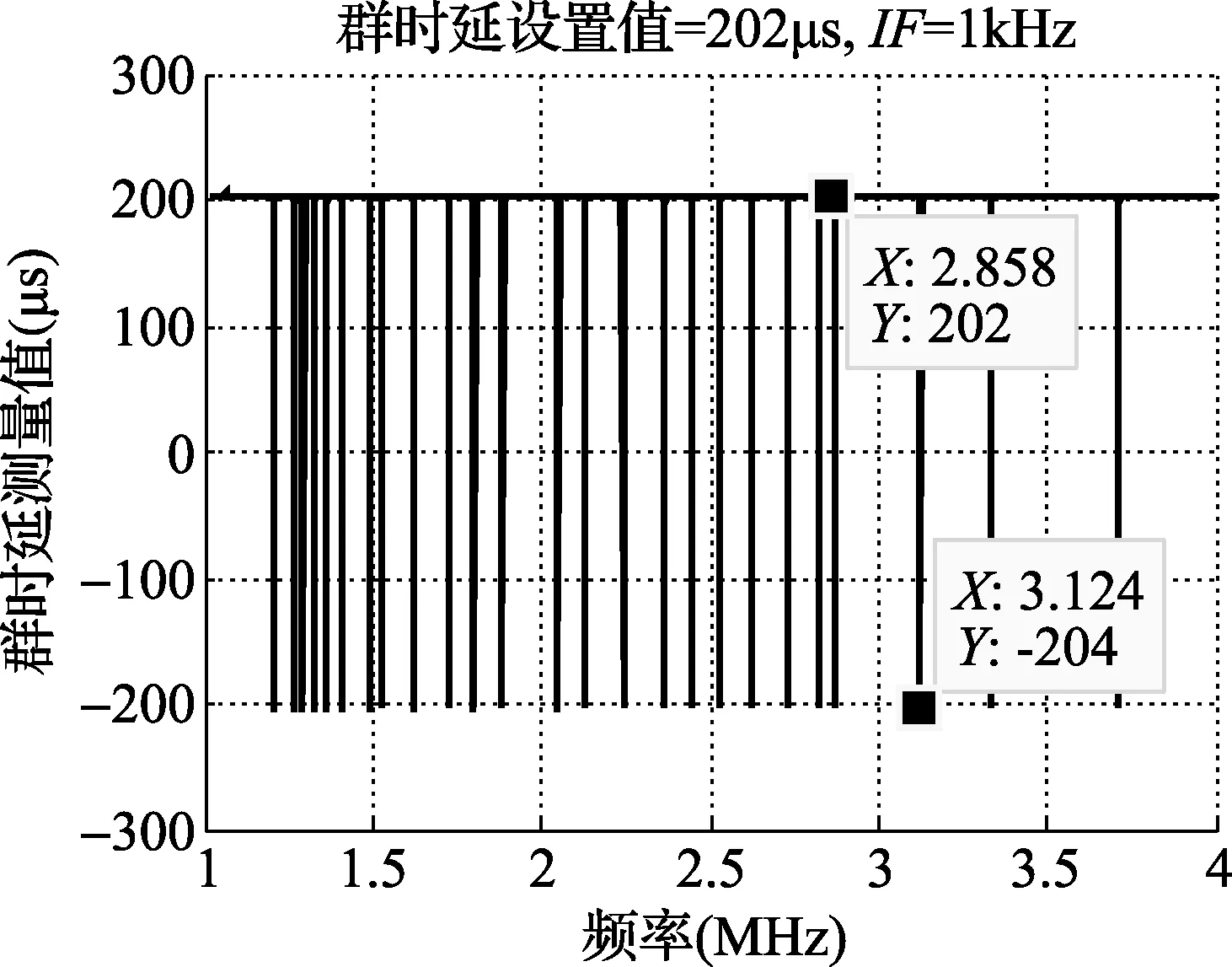
图1　群时延测量结果(第一组参数)

图2　群时延测量结果(第二组参数)

然后设置第二组参数：群时延205.1μs，矢量网络分析仪中频带宽IF=100Hz，扫频带宽100kHz～4MHz，扫频点数1601。则测量结果如图2所示。

显然在若干频段和频点上，图1和图2所示曲线包含异常测量结果，其原因是什么，如何解决，需要研究。

2　理论分析

假设实际被测群时延是D，使用矢量网络分析仪，基于相移法测量群时延，那么假设测量频点是f，而频率孔径是Δf，则该频点相移是P1：

P1=mod(2pfD,2p )

(1)

其中，mod是求余函数，在矢量网络分析仪扫频序列中与该点相邻频点的相移是P2。

P2=mod[2p (f+Δf)D,2p ]

(2)

那么测量得到的群时延是Dm：

(3)

式(3)中网络分析仪扫频频率孔径是Δf：

(4)

式(4)中SPAN是指扫频范围，Ns是指扫频点数。理论分析表明，由于mod函数的作用，导致在一些频点上出现相位从2p 到0的跳变，从而导致了图1和图2所示曲线的跳变现象，且该分析可以通过数值计算来验证。且关于相位模糊的问题，相关矢量网络分析仪的说明文档指出减小扫频SPAN、增加扫频点数有助于改善该问题，但是缺乏严谨的理论推导。

3　群时延测量约束条件的推导

从第2节分析可知，在测试设置满足一定的条件时，是可以得出正确的群时延测量结果的，下面就来推导这个约束条件。就式(3)中参与运算的一些量，可以进行以下形式变换：

fD=⎣fD」+ρ1=N1+ρ1

(5)

fD+ΔfD=⎣fD+ΔfD」+ρ2=N2+ρ2

(6)

式(5)和式(6)中⎣」运算符号指向下取整，则N1和N2都是向下取整得到的整数，则ρ1和ρ2都是一个[0，1)区间上的数，则正确测量就是要满足测量值和实际值相等，即Dm=D，那么据此来推导约束条件。在满足Dm=D的条件下，结合式(3)～ 式(6)可得：

(7)

则：

ΔfD=ρ2-ρ1

(8)

式(6)和式(5)相减得：

ΔfD=(N2-N1)+(ρ2-ρ1)

(9)

式(8)和式(9)相减得：

N1=N2

(10)

则分析得出：N1=N2是正确测量群时延的一个充要条件。我们将fd称为群时延的本征频率，定义如式(11)所示：

(11)

式(5)、式(6)、式(10)和式(11)联立得到：当f在Kfd附近时(K是正整数)，就会产生相位模糊，假设导致相位模糊的频率区间是(KfD-fs,KfD+fs)，为了测试的便利，希望fs不要太大，可以认为fs=Δf，但在实际测量中为了留有余量，可以认为“相位模糊频段”是(KfD-LΔf,KfD+LΔf)，一般可以设置为L=2。则群时延测量的约束条件就是：矢量网络分析仪SPAN的设置应当满足式(12)。

KfD+LΔf≤f≤(K+1)fD-LΔf

(12)

在具体的操作中，可以将扫频SPAN的起点设置为KfD+LΔf，终点设置为(K+1)fD-LΔf，且式(12)的约束条件还与频率分辨率Δf有关，即与扫频点数Ns有关。

4　实验验证

为了验证第3节提出的测量约束条件，进行了实验验证，使用R&S AMU200A基带衰落模拟器对输入信号设置了一个群时延值，然后，使用Agilent E5061B 矢量网络分析仪来测量该群时延值，矢量网络分析仪的SPAN和扫频点数设置依据式(12)的约束条件，在不同的群时延设置值条件下测量结果如图3和图4所示。

图3　约束条件下的群时延测量值(群时延设置值10μs)

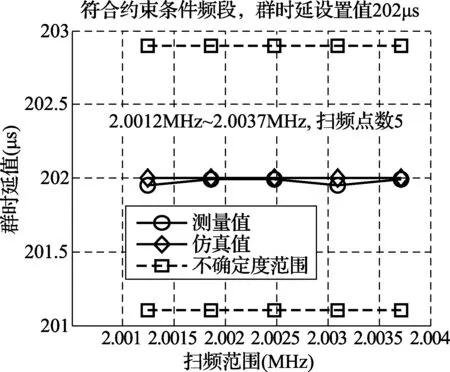
图4　约束条件下的群时延测量值(群时延设置值202μs)

为了进一步验证式(12)所示约束条件，还基于式(1)～ 式(3)的流程计算得到群时延的仿真值，一同显示在图3和图4中。显然，仿真和测量都表明，本文推导得到的群时延测量约束条件是正确的。

从式(12)所示的约束条件可以看出，扫频SPAN避开群时延的本征频率fd的整数倍的前提下，只要减小频率孔径，就可以最大限度地减小“相位模糊频段”。当然，频率孔径越小，群时延测量的不确定度就越大，应当根据具体的测试需求进行权衡。

5　结论

本文就使用矢量网络分析仪测量群时延的测量结果异常问题，进行了理论分析，明确了一些情况下相邻频点相移从2p 到0的跳变是导致测量结果异常的原因，因此，在测量中应当避开这些频点(段)。基于此，推导了群时延测量的“相位模糊频段”和约束条件，约束条件以不等式的形式给出，包括对矢量网络分析仪扫频带宽(SAPN)和频率孔径的约束。

该约束条件数学表达式的前提是已知群时延的预期值或真值，且该预期值在规定频段上是应当是一个常量。所以在使用矢量网络分析仪测量传输通道如信道模拟器、延时线等的群时延时，该约束条件尤为适用。

[1]Agilent Technologies.Printed Version of PNA Series Network Analyzer Help User’s and ProgrammingGuide(Supports Firmware A.08.00)[R].March 12，2008，P405

[2]Zhang Rui，Zhou Feng，Guo Long-qing，Wang Nan.A Nonlinear Smooth Algorithm for Measurements Curve of Group Delay[C].IEEE 73rd ARFTG Measurements Conference Digest，pp 25-28，JUN 12，2009 .Boston，USA

[3]Rohde & Schwarz GmbH & Co.KG.R&S®AMU200A Baseband Signal Generator and Fading Simulator Operating Manual[R].2012

[4]张睿，周峰，郭隆庆，王南.一种新的群时延测量曲线平滑算法[J].现代测量与实验室管理，2009(1)

[5]周峰，张睿，郭隆庆，王南.调制信号频谱测量值性质分析[J].计量技术，2009(7)

[6]周峰，张睿，郭隆庆.一种用于示波器测量EVM的相位同步算法[J].计量技术，2011(2)

[7]卢娟，李智.基于矢量网络分析仪实现微波器件的群时延测量[J].计量技术，2013(7)

[8]刘涛.群时延的快速测量方法[J].电波科学学报，2009，24(2)