基于核局部线性嵌入的基因表达谱数据分类
王 年, 许鸿洋, 梁 栋, 鲍文霞
(安徽大学 计算智能与信号处理教育部重点实验室, 合肥 230039)
随着生命科学和信息科学的发展,研究人员将生物学问题转化为模式识别问题,并将基因表达谱应用于基因组分析,挖掘出肿瘤组织中的病变基因,从而准确识别出肿瘤类型;但基因表达谱数据具有样本小,维数高,噪声大的特点[1]。直接使用数据进行肿瘤特征分析是不可行的[2, 3],须对数据进行降维处理,在获得最优特征的同时丢弃一些冗余信息,以降低数据的维数和系统的复杂性。
目前数据降维方法分为线性和非线性,常见的线性降维方法有独立分量分析(ICA)、线性判别分析(LDA)、主成分分析(PCA)等。线性降维方法的算法复杂度较低,但应用于非线性分布的数据时,降维效果较差,因此需要采用非线性方法对数据进行维数约减。流行学习是常见的非线性方法,如拉普拉斯本征映射(LM)[4],局部线性嵌入(LLE)[5]和等距映射(ISOMP)[6]等。Roweis等针对非线性数据提出基于LLE的无监督数据降维方法,能够使高维空间中的数据点映射到低维流行空间中,同时降维后的数据保持了原有数据的拓扑结构;近年来,针对 LLE算法存在的相似度度量、邻域的选取及对新样本的泛化能力等问题,各种改进方法被陆续提出,Zhang等通过将图像的相似度计算引入到LLE中,用以取代传统的欧式距离准则[7];Liu等提出有监督的局部线性嵌入算法(Supervised local linear embedding),在保留样本的流行结构的同时引入样本的类别信息,在人脸识别中取得了较好的效果,但仍然无法解决新样本泛化问题[8];Nicholos等提出LLE+SVM分类方法,在参数最优的情况下, 可以获得较好的分类结果[9];Cai等提出LLE+LBP用于人脸识别,通过调节参数以增强对新样本的泛化能力[10];Pan等提出基于权值的无监督的局部线性嵌入方法,用于深度挖掘数据的内在结构,并成功应用于人脸识别中[11];Zhao等提出基于概率分布的LLE肿瘤识别方法,通过计算样本间互为近邻的概率,再结合LLE算法,选取概率大的样本作为近邻样本[12];Andres等将数据划分为N个区域,通过求得区域最优解来获得全局最优解,但该算法未能充分的利用样本的类别信息[13]。
LLE/SLLE算法对近邻数的选择具有较高的依赖性,且通过试凑法进行参数的选择,具有偶然性且耗时。本文算法通过对欧式距离函数进行修改,将高斯核技巧引入到肿瘤识别之中,结合样本的类别信息,为样本自动设置合理的近邻,很好地解决了邻域选取问题,使得邻域中大部分为同类样本,有效地对数据进行降维及待测样本的分类;降低标准LLE/SLLE算法中对噪声和稀疏数据的敏感性。最后,通过与已有算法的对比,验证本文方法的实时性和准确性。
1 LLE和SLLE算法
1.1 LLE
设预处理后的基因表达谱数据为D维向量X={x1,x2,L,xm},x∈RD,LLE通过将高维数据集D映射到低维空间Rd,得到m个d维向量yi,i=1,2,L,m,yi为xi在d维空间的表示,且d≪D。
LLE算法主要分为3个步骤:
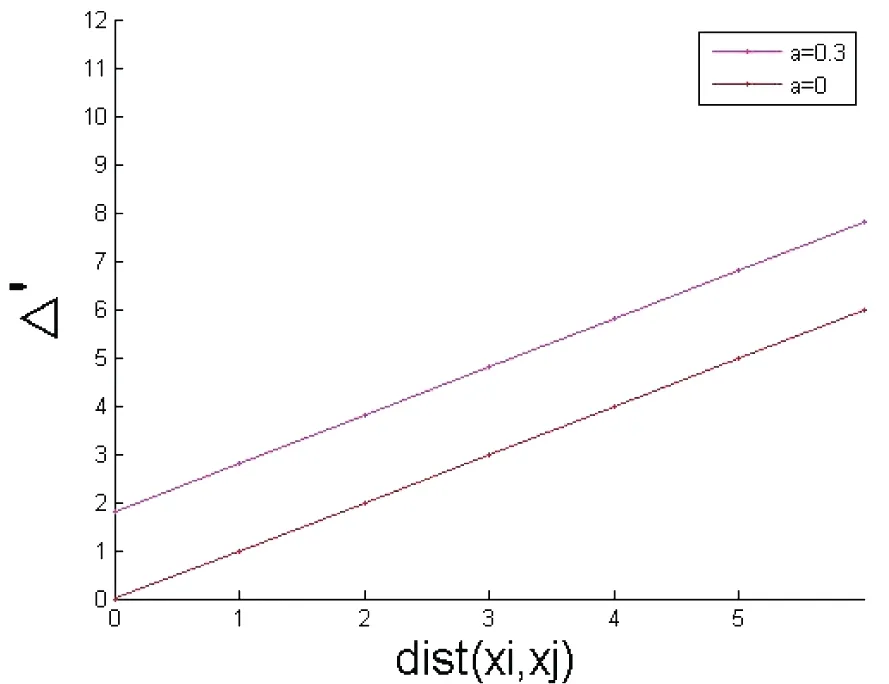
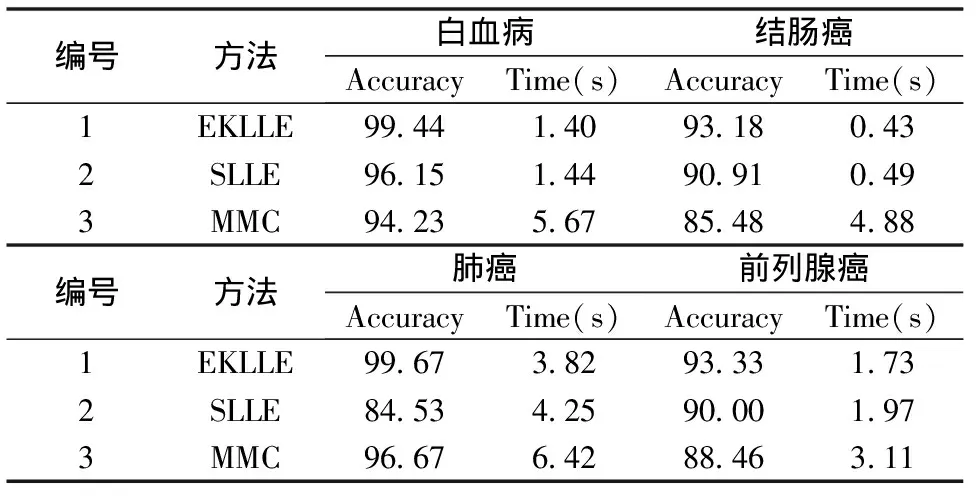
1)邻域选取,计算任意样本xi与其他(m-1)个样本间的距离,距离越小说明两样本间相似度越高,据此可确定样本xi的k(k 2)对任意样本xi,用其近邻样本的线性组合来表示xi,且使得重建误差最小化,即求式(1)的最优解; (1) (2) 3)通过求解局部重建权重矩阵,得到低维嵌入向量yi,该过程通过最小化重构误差和来实现,即式(3): (3) 利用Langrage乘数法,式(3)可转化为式(4)的特征值求解问题: MY=λY (4) 其中M=(I-W)T(I-W);取M的(2▯d+1)个最小特征值所对应的特征向量作为低维嵌入向量集Y。 LLE是一种局部线性逼近的无监督的数据降维算法,无法充分利用肿瘤样本的类别信息,使得算法对于稀疏数据和含噪声数据处理效果较差。 针对LLE算法未能充分利用样本的类别信息,Ridder等[14]提出了有监督的LLE算法;LLE根据欧式距离来获得k个近邻样本,而SLLE在欧式距离基础上增加样本点的类别信息,通过式(5)来计算R个近邻样本点。 Δ=dist(xi,xj)+αmax(dist(xi,xj))Λij,α∈[0,1] (5) (6) 其中dist(xi,xj)为欧式距离;α(0≤α≤1)为经验参数,根据数据的稀疏程度适当调节α的值,当α=0时,LLE和SLLE相同。 本文对SLLE的度量公式进行修改,将核方法引入到SLLE算法中,其主要思想是在核空间中结合样本的类别信息来确定样本的近邻域,计算后类内样本点间距离较小,类间距离较大,算法中引入了高斯核函数,如式(7)所示: (7) 对任意给定样本点(xi,Li),xi∈RD,距离公式(5)可修改为如式(8)所示: (8) 其中参数sigma大小根据数据的稀疏程度适当调节,Lj为样本的类别。图1为EKLLE与SLLE距离公式曲线图。 图1(a) EKLLE 图1(b) SLLE 由图1(a)及公式(8)知,引入样本的类别信息后,随着欧式距离的增加,EKLLE算法中类间距离的增长速率远大于类内距离,使得具有鉴别能力的数据得以表达,当含有噪声数据时,Δ′增长较为缓慢,减少了噪声的干扰,更适合含噪声数据样本分类[15]。由图1(b)及公式(5)可知,随着欧式距离的增加,SLLE算法中类内样本间与类间样本间的距离均是线性增长的,且斜率相同,使得具有鉴别能力的数据无法表现出来;其次,SLLE算法中Δ∈[0,+∞],对于含有较强噪声的数据,易造成样本邻域混乱,影响实验效果。 LLE算法中只有邻域样本参与重构,因此近邻数k的选择尤为重要,对于分布不规则且噪声大的数据,若k值选取过大,易造成非近邻数据点误归为邻域中,且易造成回路问题;若k值选取过小,则很难保证数据的整体几何结构;本文根据肿瘤基因数据的结构特点,以样本的平均相似度为阈值来自动划定样本的邻域; 设基因表达谱数据样本X={x1,x2,……,xm}两两样本间的相似度定义为式(9): S(xi,xj)=1/Δ′(xi,xj) (9) 对任意样本点xi(i=1,2,L,m)到所有样本的平均相似度为: (10) 其中dmean(i)作为判别xj是否为xi近邻的阈值,若S(xi,xj)>dmean(i),则xj为xi的近邻,否则xj不是xi的近邻,这样有效的避免了邻域过大或过小问题,保证数据的整体几何结构。近邻数k一般比高维数据的本质维数d大,这样使得样本邻域间存在一定的重叠区域,从而使得m个邻域相关联,易于恢复数据的全局结构。 设G′={g1,g2,……,gn}表示样本中所有基因所构成的集合,其中gj(1≤j≤n)代表每一个基因,n代表基因的总个数;设X={x1,x2,L,xm}代表m个样本,xi(1≤i≤m)代表某一条件下所有样本的表达值,m代表样本的个数。 基因表达谱数据具有维数高,样本少,冗余信息多,易导致分类结果偏置,本文采用Bhattacharyya距离对数据进行预处理,即式(11): (11) 表1 实验数据集样本描述 本文所用数据为急性白血病(Leukemia)、结肠癌(Colon)、前列腺癌(Prostate)和肺癌(Lung)数据集[16-19],具体描述如表1所示。 实验中, 将实验数据集分为训练集和测试集;对于结肠癌数据,训练集为40个样本(27个为T(Tumor)样本,13个为N(Normal)样本),测试集为22个样本(13个为T样本,9个为N样本)[12, 16];对于前列腺癌数据,训练集为70个样本(33个为T样本,37个为N样本),测试集为32个样本(17个为T样本,15个为N样本)。分别对结肠癌数据及前列腺癌数据采用SLLE/EKLLE进行验证,重复实验15次。图2描述了相同子空间下,不同近邻数对实验结果的影响。 图2近邻数k不同对实验结果影响 由图2可知,对于结肠癌数据和前列腺癌数据,近邻数k值过大过小均会对实验效果产生不利影响。EKLLE克服了SLLE易受不均匀稀疏数据的影响,根据样本周围数据的稀疏程度及样本的类别信息,以改进的欧式距离为自变量,为样本自动设置近邻域,避免因数据缺失而造成数据整体结构的扭曲,同时也避免近邻数太大造成的回路问题。在d=5,k=7时结肠癌正确率为93.18%,k=14时前列腺癌正确率为93.33%。SLLE对近邻数k的取值较为敏感;随着k值变化分类准确率浮动较大;结肠癌和前列腺癌数据集内样本点的分布不尽相同, 且缺少有效的确定方法,无法使用某一固定k值,采用试凑法需要大量的时间;在结肠癌分类实验中d=5,k=11,SLLE的最高正确率仅为90.91%。 分类实验中需要确定3个变量,近邻数k,低维嵌入空间d,参数sigma。EKLLE算法中的近邻数k和低维嵌入维数d固定时,参数sigma的变化对实验结果的影响如图3所示。EKLLE算法对sigma(sigma=2∶1∶12)的变化不敏感,尽管随着sigma的增加,识别率有所浮动,但仍具有较好的识别效果,使得EKLLE算法对样本具有较好的泛化性。 图3 参数sigma对分类正确率的影响 为验证本文方法的可行性,分别在 Lung、Colon、Prostate、Leukemia数据集上进行测试, 重复实验15次;实验正确率和相应的运行时间如表2 所示。 由表2知,EKLLE算法的正确率高于SLLE和MMC算法,且EKLLE算法无需人工干预,减少试凑法所浪费的时间及计算复杂度。在d=5,k=22,sigma=6时,Lung数据的分类准确率可以达到99.67%,运行时间仅为3.82 s。EKLLE算法缓解了欧式距离重构过程中对流行结构的扭曲,保持了基因表达谱数据的内在几何结构,提高了数据降维后的效果;而SLLE采用欧式距离来构造高维样本点的邻域未必能够真实的反映基因表达谱数据的内在结构,易造成不同类别的点进入同一邻域内,影响数据的降维效果。对于较难分类的Prostate数据集,SLLE算法在d=5,k=15,α=0.5时正确率为90.00%,但其近邻数k须采用试凑法,具有偶然性,运算效率较低。较MMC相比,EKLLE算法采用核技巧与样本的类别信息相结合,所需的鉴别维数明显少于MMC,降低算法的运行时间,更具有实时性。 表2 Lung、Colon、Prostate和Leukemia实验结果 本文结合生物学与模式识别领域的相关知识, 提出了一种增强的核局部线性嵌入算法,并应用于基因表达谱数据分类中。该算法充分利用肿瘤样本的类别信息和高斯核函数来改进LLE/SLLE算法中距离的度量公式,无需人工干预,通过样本点周围数据几何分布自动设置合理的近邻数,弥补了LLE/SLLE算法耗时的缺点,EKLLE比LLE及SLLE算法中使用相同的近邻数更加合理;且该方法对参数和噪声不敏感,在Colon、Lung、Prostate和Leukemia的实验结果证实了本文所提算法在肿瘤基因表达谱数据分类方面的鲁棒性和优越性,与其他方法相比,更具有现实意义。 参考文献: [1]Golub T R, Slonim D K, Tamayo P, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring [J]. Science, 1999, 286(5439): 531-537. [2]Thomas A, Thobault H, Yves V D P, et al. Robust biomarker identification for cancer diagnosis with ensemble feature selection methods [J]. Bioinformatics, 2010, 26(3):392-398. [3]Lee C P, Leu Y. A novel hybrid feature selection method for microarray data analysis [J]. Applied Soft Computing, 2011, 11(1):208-213. [4]Tu S T, Chen J Y, Yang W, et al. Laplacian eigenmaps-based polarimetric dimensionality reduction for SAR image classification [J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 170-179. [5]Roweis S T, Saul L K. Nonliner dimensionality reduction by locally linear embedding [J]. Science, 2000, 290 (5500): 2323-2326. [6]Tenenbaum J B, Silva V D, Langford J C. A global geometric framework for nonlinear dimensionality reduction [J]. Science, 2000, 290(5500): 2319-2323. [7]Zhang L J, Wang N. Locally linear embedding based on image Euclidean distance[C]. IEEE International Conference on Automation and Logistics, 2007: 1914-1918. [8]Liu C, Zhou J L, He K, et al. Supervised locally linear embedding in tensor space[C]. Third International Symposium on Intelligent Information Technology Application, 2009, 3:31-34. [9]Nichols J M, Bucholtz F, Nousain B. Automated, rapid classification of signals using locally linear embedding [J]. Expert systems with applications, 2011, 38(10): 13472-13474. [10]Cai L B, Ying Z L. Face recognition with locally linear embedding on local binary patterns[C]. Internation Conference on Information Science and Engineering, 2009, 1246-1249. [11]Pan Y Z, Ge S Z S, Mamun A A. Weighted locally linear embedding for dimension reduction [J]. Pattern Recognition, 2009, 42(5): 798-811. [12]Zhao L X, Zhang Z Y. Supervised locally linear embedding with probability-based distance for classification [J]. Computer and Mathematics with Application, 2009, 57(6):919-926. [13]Andres A M, Juliana V A, Genaro D S. Global and local choice of the number of nearest neighbors in locally linear embedding [J]. Pattern Recognition Letter, 2011, 32(16):2171-2177. [14]de Ridder D, Kouropteva O, Okun O, et al. Supervised locally linear embedding [J]. Artificial Neural Networks and Neural Information Processing, 2003, 2714: 333-341. [15]Geng X, Zhan D C, Zhou Z H. Supervised nonlinear dimensionality reduction for visualization and classification [J]. IEEE Transaction on Systems, Man, and Cybernetics, 2005, 35(6): 1098-1107. [16]Wang H Q, Huang D S. Regulation probability method for gene selection [J]. Pattern Recognition Letters, 2006, 27(2): 116-122. [17]Zhang H P, Song X F, Zhang X B. Identifying disease genes from gene expression data based on singular value decomposition [C]. International Conference on Biomedical Engineering and Information, 2011, 3: 1743-1747. [18]Wang B Y, Xu H Y, Wang N, et al. A recursive information gene selection using improved laplacian maximum margin criterion[J]. Journal of Information and Computational Science, 2013, 10(14): 4435-4443. [19]Kulkarni A, Kumar B S C N, Ravi V, et al. Colon cancer prediction with genetics profiles using evolutionary techniques [J]. Expert Systems with Application, 2011, 38(3): 2752-2757.

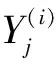
1.2 SLLE
2 改进的SLLE算法
2.1 改进的度量公式

2.2 自动选择近邻
3 实验结果
3.1 数据预处理
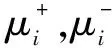

3.2 实验结果与分析


4 结束语

