关于分段函数求导数的教学思考

黄金城

（河海大学数理教学部，江苏常州213022）

分段函数在高等数学所研究的函数中是一类比较特殊的函数.分段函数在分段点的极限存在性，连续性以及可导性[1]，是高等数学教学的一个重要内容，也是学生学习的一个难点.对于分段函数求其导数时，一般地首先讨论在每一分段开区间内部的可导性，由于分段函数在其分段区间上是初等函数，因此分段函数在每一分段区间上的导数可以直接用求导公式及求导法则计算；然后用定义判断分段点处左右导数是否存在且相等；最后归纳出函数在定义域上的导函数表达式.

很多学生对于分段函数在分段点的导数的求法及其原理感到很困惑，经常出现一些错误的做法，根本原因是对于导数的定义没有理解.如何让学生正确理解并掌握分段函数求导数的方法，已有很多建议[2-4].本人通过多年的课堂教学，总结了学生在求分段函数的导数时经常易犯的错误及其原因，并给出了解决问题的几点思考.

1 关于函数在一点处的导数公式的讨论

函数在一点x0处的导数的定义公式是用增量比的极限给出的，有两种不同的形式，分别为于分段函数，由于其在分段点x0左右两侧的表达式往往不同，需要求上述两个公式的左右极限，也就是分段函数在分段点处的左导数(x0)和右导数(x)，来判断分段函数在分段点x处的可导性.00当左右极限都存在且相等，即左导数(x0)和右导数(x0)都存在且相等时，增量比的极限才存在，也就是分段函数在分段点x0的导数f′(x0)存在.反过来，当分段函数在分段点处的左导数(x0)或右导数(x0)至少有一个不存在或都存在但是不相等时，分段函数在分段点不可导.对于公当x0=0时，两个公式用起来都非常方便，当x0≠0时，若使用公式，需要计算函数值（fx0+Δx），较麻烦.因此在求导数时，最常使用的是公式在求基本初等函数的导函数时，主要利用公式，只要将函数

在一点x0处的导数的定义公式中的点x换成任意的点x

0即可.

2 求分段函数在分段点导数时常见的错误及原因

错误一：将两个不同形式的公式中的极限过程混淆

极限过程x→1错误的改为x→0.比如

正确解法：

错误二：将左右导数公式中的函数值（fx0）分别代入不同的值

错误解法：

在求左导数时，利用当x＜0时，（fx）=x2+1计算（f0），求右导数时，利用当x≥0时，（fx）=x2-1计算（f0）.事实上，公式中的（f0）是函数（fx）在x=0处的函数值，是唯一确定的实数楚什么是相同的，什么是不同的，两个极限中（fx）是不同的，但（f0）是相同的.

正确解法：

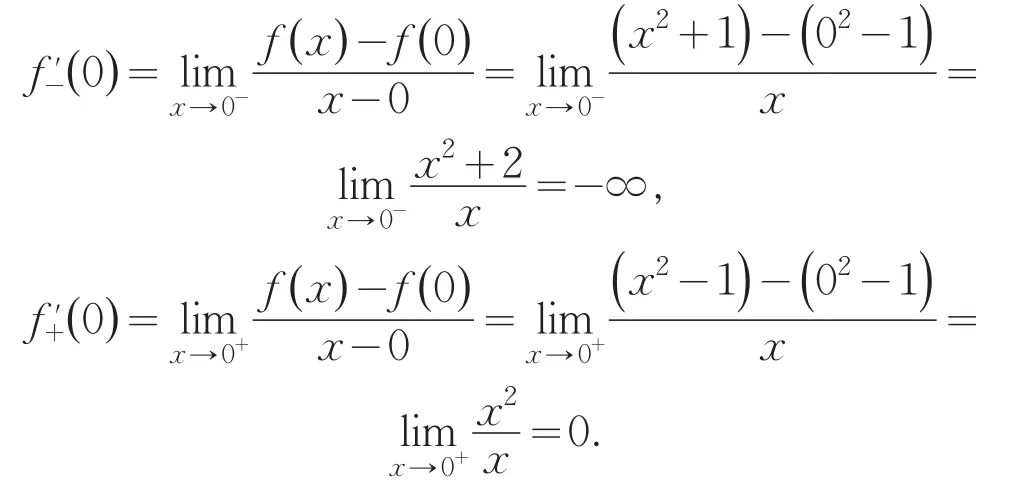
错误三：认为分段函数在分段点的导数是分段

函

正确解法：利用函数在一点处的导数的定义可以判断f（'x）在x=0处是可导的.因为

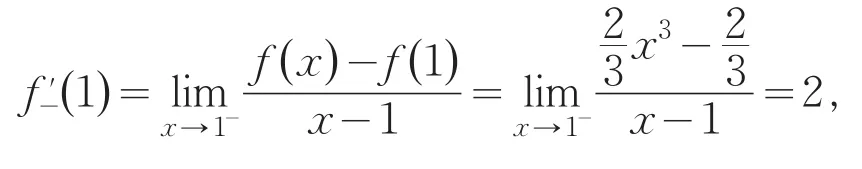
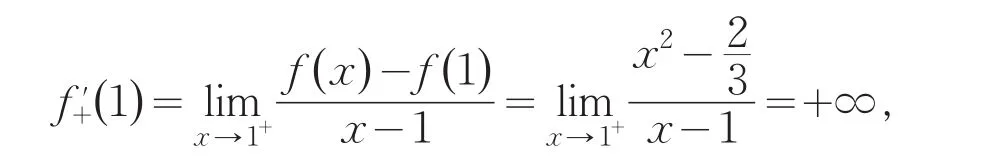
显然函数f（x）在x=1处不可导.如果先求了右导数，左导数不需要求，就可以判断f（x）在x=1处不可导，因为f（x）在x=1处的右导数不存在，而只要一个单侧导数不存在，分段函数在该分段点就不可导.综上可得

3 教学建议

为了避免学生在对分段函数求导数时出现以上错误，除了在讲解导数的定义要求学生理解定义以外，在讲解例题时，可以有针对性的列举一些错误的做法，让学生指出其中的错误，并加以修改，这样可以使学生印象深刻，从而在做题时避免采用类似的错误方法.

[1] 同济大学数学系.高数数学[M].6版.北京:高等教育出版社,2007.

[2] 刘晓妍.关于单侧导数的一种求法[J].高等数学研究,2006,9(5):26-27.

[3] 陈茜.浅谈分段函数的求导[J].邢台学院学报,2010,25(2):103-104.

[4] 马胜萍.数学教学中常见求导错误的剖析[J].甘肃科技,2005,21(12):241-243.