长江重庆河段卵砾石推移质无量纲输沙率研究
楚万强,曹明伟
(1. 小流域水利河南省高校工程技术研究中心,河南开封 475003; 2. 黄河水利职业技术学院,河南开封 475003)
长江重庆河段从大渡口至铜锣峡,全长36 km,属山区性河流。河道内比降较大(0.1%~2.0%),河床组成粒径较粗(10~130 mm),相对光滑度较小(1~50),悬移质泥沙主要以冲泻质形式输移,河床变形主要受推移质输移影响。河段内设有国家一级水文站寸滩站,该站对卵砾石推移质的观测从1960年开始,1966年后取得比较完整的资料。搜集了长江委水文上游局施测的1966—2007年共3 856组数据,作为该河段研究的基础数据。
推移质输沙率是个十分复杂的问题,自法国学者P.Goodwin[1]建立现代泥沙运动力学以来,各家学者基于不同的理论基础、使用不同的结构形式,建立了各种推移质输沙率公式。E.Meyer-Peter等根据大量的系统水槽试验,得到了以拖曳力为主要参变量的经验公式[2]。20世纪50年代H.A.Einstein根据随机理论,试图运用数理统计方法精确预测泥沙运动,并首次建立了全沙挟沙力公式[3]。R.A.Bagnold[4]将西方能量平衡概念直接用于研究推移质泥沙运动的规律,根据推移质输移的水流功率理论推导了公式。据不完全统计,目前推移质输沙率公式已超过200个。韩其为[5]认为由于现有的输沙率公式太多,通过分析和验证,比较出已有的输沙率公式比给出一个新的输沙率公式更有意义。
目前,公认程度较高的几个输沙率公式的原始资料主要为水槽试验数据,大多是在底坡较小、相对光滑度较大、缓流、模型沙颗粒较细的情况下得出的,这与前文所述山区河流的特性相差极大。因此,本文以寸滩站实测资料为基础,对长江重庆河段推移质输沙率进行了分析研究。
1 基础资料处理
将搜集的实测水力、泥沙因子等资料汇总,并按流量大小,以3 000 m3/s的步长进行分级统计,共可分成22级。将各级差内的有关因子进行算术平均,得到各级的流量、流速、水深等因子代表值(表1)。
天然河道中,因水面比降难以施测,只能根据搜集到的资料(表2)拟合水面比降J与流量Q的关系。经拟合,寸滩站Q-J关系可表示为:J=3.91Q-0.073(R2=0.923)。本文输沙率计算采用的水面比降均为拟合值。

表1 寸滩站水力、泥沙因子资料分级统计结果Tab.1 Classification statistical results of hydraulic and sediment factors of Cuntan Hydrologic Station

表2 寸滩站Q-J关系搜集资料Tab.2 Collected data of Q-J of Cuntan Hydrologic Station
2 现有推移质公式对比
泥沙输移是水流运动的结果,因此水流运动的强弱与泥沙输移强度有直接关系。按照钱宁的思路[6],可将各家公式转化为推移质输沙强度Φ和水流强度Θ的函数,再直接比较其相关性的优劣。其中,推移质输沙强度:
(1)

(2)
式中:gb为推移质单宽输沙率(kg·m- 1·s-1);γs为泥沙密度(kg/m3);γ为水的密度(kg/m3);D50,D35为沙粒粒径(m),表示总质量中分别有50%和35%的沙粒小于该粒径;J为水面比降;R为水力半径(m)。
选择Meyer-Peter和Tsubaki等5个比较典型的推移质输沙率公式,分别用简化后的Φ与Θ的函数关系表示。
Meyer-Peter 推移质输沙率公式:Φ=(4Θ-0.188)3/2
(3)

(4)
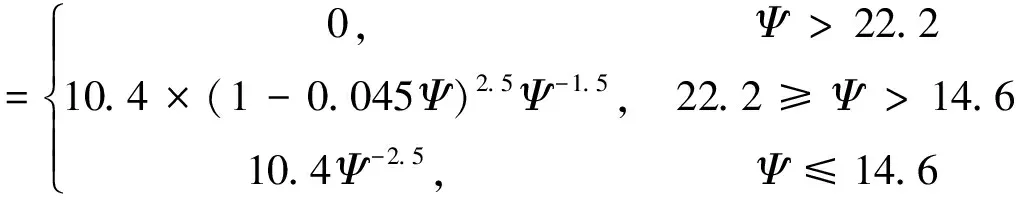
(5)
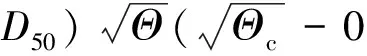
(6)

(7)


图1 现有推移质输沙率公式比较Fig.1 Comparison of existing formulas for bed load discharge
根据实测水流泥沙资料(表1),采用上述公式分别进行计算,比较实测值Cm和计算值Cc(图1),以及平均分散率:
(8)
式中:Ri为每组数据的分散率,Ri=Cc/Cm。
从各公式对长江寸滩站无量纲输沙率描述精确性来看,Meyer-Peter公式的临界起动水流强度Θc=0.047,大于大比降粗颗粒卵砾石的Θc=0.027 5Fr,导致计算值偏小;Ackres&White和Fredsoe公式的Θc=0.029,与Θc=0.027 5Fr较为接近,这两个公式的计算值也最为接近;Tsubaki公式将Θc定义为无因次起动切应力,在中小输沙强度时,该式计算值较大,随着输沙强度的增大,计算精度逐渐提高;Graf公式采用按水流强度分段描述输沙率,且未考虑Θc对输沙率的影响,导致该式在中小输沙强度时的计算值偏大。
5个公式的计算值平均分散率依次为0.71, 2.24, 1.88, 0.82和0.84,可见Meyer-Peter,Tsubaki,Graf公式的计算值精确度较差, Fredsoe公式的计算值与实测结果最为接近,Ackres & White公式次之。
3 长江重庆河段推移质输沙公式
3.1 重庆河段推移质输沙公式拟合
由于重庆河段流量、比降、流速、床面切应力大,流态急,水动力条件强有利于推移质的运动,同时,该河段的河床组成主要为粒径较大的卵砾石,使床沙难以起动,这两类导向相反的因素综合作用,导致传统公式不能很好地描述其输沙规律[8],因此有必要在经典公式的基础上对其系数进行修正。同时,由于Fredsoe公式的计算精度最高,可根据该公式的推导原理,结合实测数据,优化公式系数,得出适合长江重庆河段的输沙率公式。

(9)

图2 长江重庆河段输沙率公式系数确定Fig.2 Determination of parameters for bed load discharge of the Chongqing reach of the Yangtze River
根据寸滩水文站实测数据(表1)对式(9)进行拟合,拟合结果见式(10),从拟合效果来看,22组数据中有13组数据与实测值的误差率小于10%,拟合数据的残差平方和为0.882(图2),平均分散率为0.91,拟合精度较传统公式有了进一步提高。
(10)
3.2 重庆河段推移质公式计算精度对比
魏丽等[10]认为推移质输沙率与水流流速的高次方成正比,并针对重庆河段的河段特性,以水流流速为主要参数建立单宽推移质输沙率计算式:
(11)
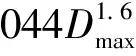

图3 重庆河段推移质输沙公式计算精度对比Fig.3 Comparison of formulas
根据表1所列实测水力要素,依次代入式(11)及式(1),可得相应的输沙强度,并与本文计算式计算值进行对比,将结果点绘于图3。
由图3可见,魏丽公式计算值在Φ<10-3时要略大于实测值,在Φ>10-3时,逐渐偏离分界线,数倍小于实测值。本文计算式则能较好地分布在分界线两侧。这主要因为魏丽公式以水流流速作为公式计算的主要参数,然而天然河流中,与推移质输沙率关系密切的近底流速难以施测,在实际研究中往往用近表面的平均流速代替,同时,输沙率增大是河段流速增大的结果。近底流速的增幅要大于表面流速[4],因此,输沙率越大,根据平均流速计算的输沙率误差也越大。同时,本文计算式的平均分散率0.91也要优于魏丽公式的0.83。由此可见,本文计算式能很好地代表长江重庆河段实际卵石推移质输移,采用本文计算式计算该河段推移质无量纲输沙率较以往公式计算精度有一定的提高。
4 结 语
(1)根据实测资料,将现有较经典的推移质公式与实测值对比, Meyer-Peter公式计算值较小,Tsubaki公式、Graf公式计算值则偏大,而Fredsoe公式、Ackres & White公式计算值较接近。
(2)参照Fredsoe公式的思路,以Θ与Θc为主要参数来建立输沙公式,假设推移质的输移量与水流的有效运动强度成幂次关系,得到长江重庆河段推移质无量纲输沙率计算式形式,然后通过该河段实测水力要素拟合公式内系数,得到适用于长江重庆河段的输沙率计算式。
(3)利用实测资料对各公式计算准确性进行对比,结果表明,在计算长江重庆河段输沙率时,本文计算式的精度要优于经典公式和针对该河段的魏丽公式,可为长江重庆河段推移质输沙率的计算提供参考。同时,本文的研究方法也可为同类河段输沙率研究提供借鉴。
参 考 文 献:
[1]GOODWIN P. Analytical solutions for estimating effective discharge[J]. Journal of Hydraulic Engineering, 2004, 130(8): 729-738.
[2]MEYER-PETER E, FAVRE H. Neue versuchsergebnisse über die wirkung der stickstofformen unter besonderer berücksichtigung der umweltverhältnisse[J]. Journal of Plant Nutrition and Soil Science, 1934, 103(13): 147-150.
[3]EINSTEIN H A. Formula for the transportation of bed-load[J]. Transactions of ASCE, 1942, 107(1): 561-573.
[4]BAGNOLD R A. An approach to the sediment transport problem from general physics[J]. Hydraulics of ASCE, 1966, 42(3): 1-37.
[5]韩其为. 黄河下游输沙及冲淤的若干规律[J]. 泥沙研究, 2004(3): 1-13. (HAN Qi-wei. Some rules of sediment transportation and deposition scouring in the lower Yellow River[J]. Journal of Sediment Research, 2004(3): 1-13. (in Chinese))
[6]钱宁, 张仁, 周志德. 河床演变学[M]. 北京: 科学出版社, 1989. (QIAN Ning, ZHANG Ren, ZHOU Zhi-de. Riverbed evolution[M]. Beijing: Science Press, 1989. (in Chinese))
[7]ENGELUND F, FREDSOE J. A sediment transport model for straight alluvial channels[J]. Nordic Hydrology, 1976, 7(5): 293-306.
[8]杨胜发. 内流河宽浅变迁河流水沙运动规律研究[D]. 成都: 四川大学, 2003. (YANG Sheng-fa. Characteristics of flow and sediment transport in the inner river′s broad-shallow shifting reach[D]. Chengdu: Sichuan University, 2003. (in Chinese))
[9]杨胜发, 周华君, 王兴奎. 大比降卵砾石河流输沙率试验研究[J]. 水动力学研究与进展: A辑, 2006, 21(5): 672-678. (YANG Sheng-fa, ZHOU Hua-jun, WANG Xing-kui. The experimental study on the bed-load rate of the high gradient gravel river[J]. Journal of Hydrodynamics(SerA), 2006, 21(5): 672-678. (in Chinese))
[10]魏丽, 汪鹏, 卢金友. 长江上游寸滩站卵石推移质输沙规律研究[J]. 人民长江, 2010, 41(15): 83-86. (WEI Li, WANG Peng, LU Jin-you. A study of gravel bed load transport laws at Cuntan in upper Yangtze River[J]. Yangtze River, 2010, 41(15): 83-86. (in Chinese))

