基于可靠度随机有限元法的海洋混凝土结构耐久性分析
洪 斌,杨绿峰,2,文 涛,陈 正,蒋琼明
(1. 广西大学土木建筑工程学院,工程防灾与结构安全教育部重点实验室,广西南宁 530004; 2. 广西壮族自治区住房和城乡建设厅,广西南宁 530028)
港口码头等水运工程长期处于海洋氯离子侵蚀环境中,其混凝土结构发生失效的原因大多不是结构设计的初始抗力不足或工作荷载发生了不利变化,而是结构在环境腐蚀作用下发生了耐久性破坏。特别在滨海地区,海洋氯离子对混凝土中钢筋的锈蚀,是导致工程结构提前失效的重要原因。为了描述氯离子在混凝土中的表观扩散,M.CollePardi等[1]利用Fick第二扩散定律,建立了氯离子在混凝土中扩散的解析解。但是海洋混凝土结构体型及其所处环境的腐蚀作用机理比较复杂,且存在诸多不确定性,有必要依据可靠度理论综合分析不同随机因素对混凝土结构耐久性的影响[2-5]。M.Prezzi等[2]通过假定氯离子扩散系数为随机变量开展混凝土结构的服役寿命随机预测。C.G.Nogueira等[3]考虑了钢筋初始锈蚀的氯离子阈值浓度、表面氯离子浓度、不同水灰比的氯离子扩散系数以及混凝土保护层厚度的概率密度分布情况,建立了混凝土结构寿命预测的可靠度解析方法。马亚丽等[4]分析了环境作用、混凝土材料、结构几何尺寸等随机参数的概率分布特征,通过解析理论建立可靠指标和侵蚀时间之间的关系,改进了混凝土结构耐久寿命的预测方法。S.J.Kwon等[5]进一步考虑混凝土结构的时变特性,分析了保护层厚度、28 d龄期混凝土的扩散系数、表面氯离子浓度和龄期衰减系数的变异性,利用概率分析方法预测了不同裂缝宽度以及完好混凝土结构的服役寿命。但是,上述研究均是通过解析理论得到服役寿命的预测模型,而实际工程结构的极限状态方程通常属于多维、非线性问题,往往难以显式表达。更重要的是,上述研究没有能够定量回答不同随机因素对腐蚀环境下混凝土结构服役寿命的影响程度。因此有必要采用随机数值方法开展混凝土结构服役寿命的可靠度敏感性分析。
当前结构随机分析的数值方法主要有3类:蒙特卡罗法(MCS)、随机响应面法(SRSM)和随机有限元法(SFEM)。其中,MCS以确定性有限元法为基础,根据模拟技术抽样出失效样本,得到混凝土结构的失效概率[6],通常用于检验其他方法的有效性。但在小失效概率系统中,为获得足够的失效样本,需要进行海量抽样,计算工作量巨大,难以为工程实践所接受。马尔可夫链模拟法[7]能高效地模拟失效区样本点,大大减少了抽样次数,但要求随机变量的概率密度函数必须以均值为中心对称。近年发展起来的层递响应面法[8],通过遴选合理的配点和回归分析,建立显性表达的随机响应量函数,无需对结构进行大量重复计算,提高了计算效率。 随机有限元法[9]能够通过理论分析建立响应量表达式,并且能够和可靠度算法直接耦合,具有简便实用、计算效率和计算精度较高的优点。
鉴于上述分析,本文采用随机有限元和可靠度方法建立了氯盐环境下混凝土结构服役寿命的随机变量敏感性分析模型。首先利用摄动技术建立了混凝土中氯离子扩散过程和浓度分析的随机有限元法,进而依据钢筋混凝土结构的腐蚀诱导期建立正常使用极限状态方程,建立氯盐侵蚀下混凝土结构服役寿命分析的可靠度随机有限元法,利用灵敏系数分析混凝土结构可靠度和服役寿命对不同随机变量的敏感性。研究表明:本文建立的可靠度随机有限元模型能高效地预测氯盐侵蚀下混凝土结构的服役寿命,而且能够定量地比较不同随机因素对混凝土结构服役寿命的影响程度。
1 海洋混凝土结构中氯离子扩散的随机有限元法
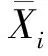
(1)
基于Fick第二定律,利用变分原理建立氯离子扩散的有限元方程[10]:
(2)
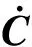
(3)
式中:N和N′分别表示单元形函数及其一阶导数[10];氯离子扩散系数D(t)具有时变性:
(4)
式中:t0为混凝土的初始暴露龄期;D0为t0时刻的混凝土初始扩散系数,具有随机性;n为氯离子扩散系数的龄期衰减系数。
将扩散矩阵K以及浓度向量C在随机变量均值处按照二阶泰勒级数展开,合并零均值随机变量ξ的同次项系数,并舍去二阶以上的摄动微量,可得氯离子随机扩散分析的随机有限元递归方程:
(5)
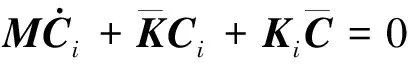
(6)

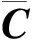
(7)
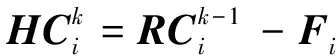
(8)
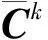
(9)
(10)
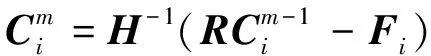
(11)
2 海洋混凝土结构可靠度的PSFEM优化迭代法
2.1 混凝土耐久性极限状态方程
一旦混凝土中保护层厚度d处的氯离子浓度Cd达到钢筋脱钝腐蚀的阈值浓度Cr,混凝土中的钢筋将因表面钝化膜受到破坏而开始腐蚀,混凝土结构的耐久性和正常使用功能将受到影响。因而基于正常使用状态,混凝土结构的极限状态函数为:
(12)
式中:X表示由功能函数中的m个随机变量(包括初始扩散系数D0,保护层厚度d,表面浓度CS以及阈值浓度Cr)组成的随机向量,其协方差矩阵为CX。
若随机变量X具有相关性,通过正交变换法,可将X转换为一组标准不相关的随机变量:
(13)
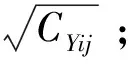
(14)
对式(13)求逆变换,并代入极限状态方程(12),即可得由不相关的标准随机变量Z表示的极限状态函数:
(15)
2.2 可靠指标分析的梯度优化法
结合式(12),可以求得氯盐侵蚀下混凝土结构正常使用极限状态函数式(15)在验算点Z*处的梯度:
(16)
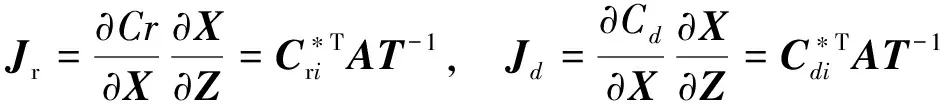
(17)
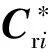
沿着极限状态面上验算点处的梯度方向,可确定第k迭代点的移动方向α和移动步长s:
(18)
(19)
通过迭代计算可得到新的验算点:
(20)
设定收敛容差ε,若由式(20)得到的Zk+1代入式(15)满足G(Zk+1)<ε,可认为验算点在极限状态曲面上。由此可得到可靠指标βk+1:
(21)
当[(βk+1-βk)/βk]<ε时,得到的βk+1即为混凝土结构的可靠指标。
3 海洋混凝土结构的服役寿命及其参数敏感性分析
混凝土结构的服役寿命是工程耐久性设计关注的重点,通过计算混凝土结构不同服役时间的可靠指标,建立混凝土结构可靠指标随侵蚀时间变化的关系曲线。当指定了混凝土结构满足预期功能目标的可靠指标后,以此为基准,在关系曲线图中作出可靠度水平直线,与曲线交点的横坐标即为结构耐久性低于规定可靠指标的时间,以此作为氯离子侵蚀下混凝土结构满足该可靠度水平的服役寿命。
通过可靠指标的求解以及规定确定的可靠度水平,可以直接获得混凝土结构的服役寿命。因此混凝土结构的服役寿命与可靠指标受随机参数的影响程度相同,具有正相关性。可以利用可靠度的参数灵敏性分析混凝土结构服役寿命对随机参数的敏感性。
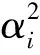
4 算例分析
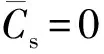
为了验证本文方法的正确性,将各随机变量在不同变异系数下由RSFEM得到的可靠指标与MCS结果进行比较(见图2)。从图2中可以看出,两种方法吻合良好,由此证明了本文建立的可靠度随机有限元法具有较高的精度。从图2中还发现,随着变异系数的增大,防护堤混凝土结构的可靠指标降低。因此,在实际工程中,若对施工等环节进行合理的质量控制,使制备得到的混凝土材料以及结构参数的离散性降低,可降低随机参数的变异性,从而提高混凝土结构的可靠度。
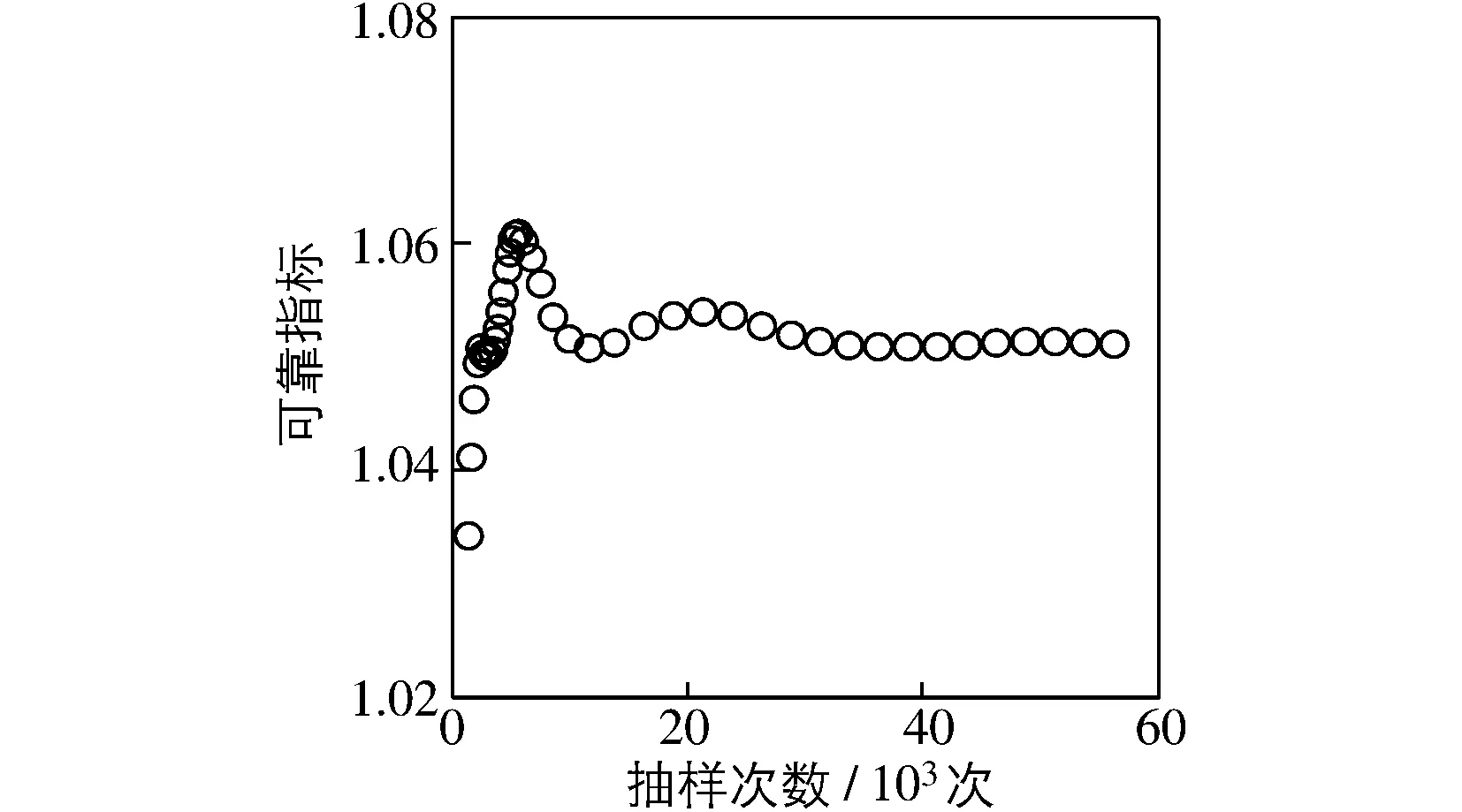
图1 MCS抽样的可靠指标Fig.1 Reliability index by the MCS
通过对计算机运算程序所耗费的时间进行统计,这里使用Lenovo启天M690E计算机(Intel(R) Core(TM)2 Duo CPU E7400 @ 2.80GHz 2.79GHz,2.00GB内存)。比较RSFEM与抽样5万次的MCS在变异系数为0.1、服役50年时的计算时间,前者计算耗时仅有7.8 ms,而后者的耗时长达10 457.8 ms。可见RSFEM具有较高的计算效率,适宜于工程应用。
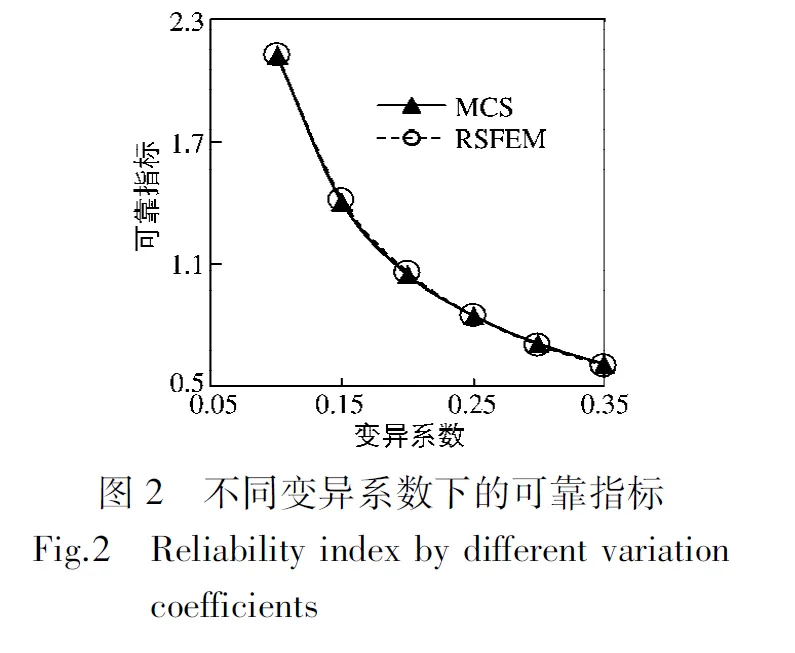
进一步利用RSFEM计算防护堤结构在不同变异系数(δ)、不同服役时间的可靠指标,结果如图3所示。由图可见,混凝土结构的可靠指标随变异系数的增大、服役时间的增长而降低。
根据《工程结构可靠性设计统一标准》GB50153-2008建议,对不可逆的正常使用极限状态的可靠指标取为1.5。因而在图3中作可靠度水平β=1.5直线,与图中其他曲线交点的横坐标就是该可靠度水平下与不同变异系数相应的防护堤结构服役寿命,从图中可以看出,混凝土结构的服役寿命随变异系数的增大而减少。由于工程施工中,一旦混凝土质量控制不好,将会增大混凝土材料性能的随机变异性,从而降低混凝土结构的服役寿命,严重时甚至无法达到设计使用年限。
考虑随机变量之间的相关性,对各随机变量间的相关系数(ρ)取相同值,分别在低度线性相关(ρ=0.2)、显著线性相关(ρ=0.5)和高度线性相关(ρ=0.8)时,计算防护堤结构服役不同时间的可靠指标,并与随机变量不相关(ρ=0)的结果进行比较,当随机参数变异系数取0.1时计算结果如图3(b)所示。可见,混凝土结构的可靠指标随相关系数的增加而增大;随机变量间的相关系数越大,混凝土结构的服役寿命越长。
(a) 不同服役时间的可靠指标 (b) 不同相关系数下的可靠指标图3 不同服役时间和不同相关系数下的可靠指标Fig.3 Reliability index given by different service lives and different correlation coefficients
为分析各随机变量本身对混凝土结构服役寿命的影响,逐一将各随机变量的均值提高10%,保持其变异系数为0.1不变,并计算此时的混凝土结构服役寿命(图4)。从图4中可见,当提高表面氯离子浓度CS或混凝土暴露初始时刻的氯离子扩散系数D0的均值时,混凝土结构的服役寿命将随之降低;而提高阈值浓度Cr与混凝土保护层厚度d的均值时,混凝土结构的服役寿命将随之提高。其中,保护层厚度d引起的服役寿命改变量最大,其次为D0、阈值浓度Cr以及表面氯离子浓度CS。也就是说,保护层厚度和氯离子扩散系数对氯盐侵蚀下的混凝土结构服役寿命的影响最大。因此,为延长混凝土结构的服役寿命,可以在规范许可的范围内,尽可能取更大的保护层厚度,并降低混凝土的氯离子扩散系数。
进一步分析参数的随机性对混凝土结构服役寿命的影响,这里从参数CS,Cr,D0和d任意选取一个,考虑其随机性,计算变异系数为0.1时混凝土结构的服役寿命,并与同时考虑上述4个参数随机性时混凝土结构的服役寿命相比较,结果见图5。
从图5可见,同时考虑4个参数的随机性时,混凝土结构的服役寿命最短。而忽略任一随机参数的随机性,都会高估混凝土结构的服役寿命,导致结构设计不安全。 同时,混凝土保护层厚度d的随机性对结构服役寿命影响最大,其次是氯离子扩散系数,再次是钢筋脱钝锈蚀的阈值浓度,对混凝土结构服役寿命影响最小的是表面氯离子浓度。因此,在混凝土结构的耐久性设计和施工中,要保证足够的混凝土保护层厚度。

图4 服役寿命随均值的改变 图5 不同变异系数下的服役寿命 Fig.4 Service life change with mean value Fig.5 Service life by different variation coefficients
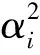
由于龄期衰减系数的取值在一定程度影响到混凝土扩散系数、进而影响到不同随机变量的可靠度重要性系数,因此需要分析高性能混凝土的龄期衰减系数在正常取值范围n=0.2~0.5之间变化时随机变量重要性的排序,变异系数取0.1时的计算结果如图7。由图可见,当n=0.2~0.5时,尽管各随机变量的可靠度重要因子有变化,但不同随机变量间的大小排序始终不变。

图6 可靠指标对各随机因素的重要因子 图7 不同龄期衰减系数的重要因子 Fig.6 Importance factors of random parametersto reliability index Fig.7 Importance factors to attenuation coefficients
5 结 语
本文提出了氯盐侵蚀下海洋混凝土结构服役寿命分析的可靠度随机有限元法,分析了服役寿命对随机变量的敏感性,据此揭示了混凝土的氯离子扩散系数、表面氯离子浓度、混凝土保护层厚度以及钢筋脱钝阈值浓度等对混凝土服役寿命的不同影响程度。研究表明,混凝土保护层厚度对结构服役寿命影响最大,其次是混凝土的氯离子扩散系数。
氯盐侵蚀下海洋混凝土结构的材料、几何和环境等参数的随机性都对结构服役寿命有显著影响,其中,混凝土保护层厚度的随机变异性对混凝土结构耐久性影响最大。忽略任一参数的随机性都会导致高估混凝土结构的服役寿命,使得设计成果偏于不安全。
参 考 文 献:
[1]COLLEPARDI M, MARCIALIS A, TURRIZZANI R. The kinetics of penetration of chloride ions into the concrete[J]. Cemento (Italy), 1970, 67(4): 157-164.
[2]PREZZI M, GEY S P, MONTEIRO P J M. Reliability approach to service life prediction concrete exposed to marine environment[J]. ACI Mater J, 1996, 93(6): 522-544.
[3]NOGUEIRA C G, LEONEL E D. Probabilistic models applied to safety assessment of reinforced concrete structures subjected to chloride ingress[J]. Engineering Failure Analysis, 2013, 31: 76-89.
[4]马亚丽, 张爱林. 基于规定可靠指标的混凝土结构氯离子侵蚀耐久寿命预测[J]. 土木工程学报, 2006, 39(2): 36- 41. (MA Ya-li, ZHANG Ai-lin. Durability life prediction of concrete structure based on the regulated reliability index under chloride environment[J]. China Civil Engineering Journal, 2006, 39(2): 36- 41. (in Chinese))
[5]KWON S J, NA U J, PARK S S, et al. Service life prediction of concrete wharves with early-aged crack: Probabilistic approach for chloride diffusion[J]. Structural Safety, 2009, 31(1): 75-83.
[6]施养杭. Monte-Carlo法氯离子侵蚀下混凝土构件寿命预测[J]. 华侨大学学报: 自然科学版, 2005, 10(2): 369-372. (SHI Yang-hang. Life forcast of concrete member under choride erosion by Monte-Carlo method [J]. Journal of Huaqiao University(Natural Science), 2005, 10(2): 369-372. (in Chinese))
[7]SONG Shu-fang, LU Zhen-zhou, QIAO Hong-wei. Subset simulation for structural reliability sensitivity analysis[J]. Reliability Engineering and System Safety, 2009, 94: 658-665.
[8]杨绿峰, 李朝阳, 杨显峰. 结构可靠度分析的向量型层递响应面法[J]. 土木工程学报, 2012, 45(7): 105-110. (YANG Lü-feng, LI Zhao-yang, YANG Xian-feng. Vectorial cooperative response surface method for structural reliability[J]. China Civil Engineering Journal, 2012, 45(7): 105-110. (in Chinese))
[9]杨绿峰, 胡春燕, 陈正, 等. 混凝土中氯离子随机时变扩散过程及浓度分布[J]. 建筑材料学报, 2013, 16(2): 246-253. (YANG Lü-feng, HU Chun-yan, CHEN Zheng, et al. Stochastic and time-dependent diffusion of chloride ion in concrete and its concentration distribution[J]. Journal of Building Materials, 2013, 16(2): 246-253. (in Chinese))
[10]杨绿峰, 洪斌, 高钦, 等. 混凝土结构中氯离子扩散分析的精细积分法[J]. 水利水电科技进展, 2012(4): 32-36. (YANG Lü-feng, HONG Bin, GAO Qin, et al. Precise integration method for analysis of chloride diffusion in concrete structure[J]. Advances in Science and Technology of Water Resources, 2012(4): 32-36. (in Chinese))
[11]SAASSOUH B, LOUNIS Z. Probabilistic modeling of chloride-induced corrosion in concrete structures using first-and second-order reliability methods[J]. Cement & Concrete Composites, 2012, 34(9): 1082-1093.
[12]FRIER C, SØRENSEN J D. Finite element reliability analysis of chloride ingress into reinforced concrete structures[J]. Structure and Infrastructure Engineering, 2007, 4(3): 355-366.

