小波分解高、低频双自回归模型及其在水质监测中的应用
陈吉江,毛洪翔,李鹏程,夏国团,章卫军
(1. 余姚市水利局,浙江余姚 315400; 2. 宜水环境科技(上海)有限公司,上海 200125)
目前,水质预测主要利用监测的历史数据作为初始序列或训练数据,运用不同数学逻辑方法推算在各类影响因素作用下未来水质数据的发展趋势[1]。方法有时间序列模型[2]、灰色理论模型[3]、模糊理论模型[4]、回归模型和动态系统物元模型[5],以及近年来得到应用的人工神经网络[6]等。其中,基于自回归的时间序列模型,理论基础坚实,计算方法简便,在水质预测中受到普遍欢迎,得到广泛应用。基于自回归的水质预测方法可以有多种型式,如①单一自回归模型, 即对时间序列建立单一自回归方程进行预测;②小波分解+双自回归,即预先对时间序列进行小波分解,然后对分解所得的高、低频序列分别建立各自的自回归方程,最后以高、低频自回归方程计算值的叠加值作为预测值;③自回归+卡尔曼滤波,即对单一自回归模型求得的预测值,采用卡尔曼滤波进行校正,作为最终预测值;④小波分解+双自回归+卡尔曼滤波,即对小波分解+双自回归模型求得的预测值,采用卡尔曼滤波进行校正,作为最终预测值。进行水质预测时,为了尽量提高预测的精度,要根据水库水质监测资料的实际情况,合理选择模型,这点至关重要。
一些水库的水质监测数据序列在频域上存在着明显的高频部分和低频部分。自回归预测模型的方法基于时间序列的平稳假设,对数据的平稳性要求较高。如果把时间序列看做一种信号,通过将原始信号分离成低频信号和高频信号,必然可以提高时间序列的平稳性,从而提高自回归预测模型的精度。因此,本文选择上述第2种模型,对其原理、步骤及预测成果(以梁辉水库为例)进行介绍,并与单一自回归模型预测成果进行比较。
1 小波分解高、低频双自回归模型原理
1.1 小波分解原理
水质监测数据序列的预处理采用离散小波变换,多尺度离散小波变换能将原始信号(也就是原始水质监测数据序列)进行不同时间分辨率上的分解。以分解层数n为例,其一般步骤为先将原始信号S分解为低频部分c1和高频部分d1,然后对低频部分c1进一步分解为c2和d2,以此类推,逐层分解[7]。
多尺度小波分解与重构一般通过Mallat算法实现[8]。Mallat算法理论如下:设Vj是L2(R)中的一个多分辨率的分析,φ为尺度函数,ψj,n为小波函数,Mallat算法的分解式如下:
(1)
式中:H为低通滤波器;G为高通滤波器。通过式(1)可以将原始信号分解为d1,d2,…,dj和cj(j为最大分解层数),cj和dj分别称为原始信号在分辨率为2-j的低频信号和高频信号。
为保证水质预测结果更加可靠,分解后还必须利用Mallat算法分别重构分解后的高频和低频信号[9],使它们的样本数与原信号S的样本数一致,重构描述公式如下:
(2)
式中:H*和G*分别是H和G的对偶算子。
采用上式对小波分解后的信号进行重构,且有:T=D1+D2+…+Dj+Cj
(3)
式中:D1,D2,…,Dj分别为第1层、第2层、…、第j层高频信号重构结果;Cj为第j层低频信号重构结果。
1.2 自回归模型的参数估计与检验准则原理


(4)

(5)

上述方法中,用最小二乘法进行参数估计非常简单,参数估计无偏,精度高,可表示为以下方程组:
(6)
则Φ的最小二乘估计为:φ=(xTx)-1xTY
(7)
本文则以直接最小二乘估计和Akaike信息检验准则的FPE(Final Prediction Error),AIC(Akaike Information Criterion) ,BIC 准则结合具体计算成果进行讨论。准则的具体计算公式如下:
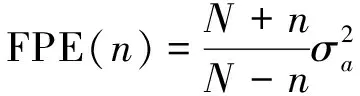
(8)
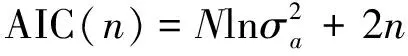
(9)
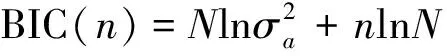
(10)
在各自的准则函数取得最小值时的模型为适用模型。
2 小波分解高、低频自回归模型
该模型建模共分以下5个步骤: ①利用多尺度小波分析理论对水质数据序列进行多尺度分解,得到数据序列的低频信号和高频信号;②通过低通滤波器和高通滤波器的对偶算子分别重构水质信号的低频部分和高频部分;③对重构后的高频信号(D1,D2,…)和低频信号(Cj)自回归模型进行定阶和参数估计,并对模型的适用性进行检验,最后分别建立J+1个自回归模型;④建立的自回归模型分别预测各层重构后的高频信号和低频信号;⑤叠加各层预测值得出下一个时刻的预测结果。
3 水库水质预测中的应用
以梁辉水库为例,详细说明小波分解高、低频双自回归模型进行水库水质预测的具体过程。梁辉水库位于余姚市梨洲街道南庙村,流域面积35.06 km2,是一座以防洪、供水为主,结合发电、水产等综合利用功能的中型水库,总库容3 152.3万m3。根据浙江省水资源监测中心余姚监测站多年的人工水质监测数据,影响其水质的主要因素为pH(酸碱度)、DO(dissolved oxygen-溶解氧)、TN(total nitrogen-总氮)、TP(total phosphorus-总磷) 。
3.1 数据与方法
选取2005年1月至2011年12月的水质指标(PH,DO,TN,TP)数据用于预测模型的建立,2012年1月至2012年12月的数据用于预测结果的对比验证。由于篇幅的限制,只以DO水质指标为例。
3.2 模型的建立与分析

(a) 低 频 (b) 高 频图1 DO 小波分解Fig.1 DO wavelet low frequency and high frequency diagram
为避免分层过多造成各层预测误差的叠加现象,故对水质监测数据序列进行一层分解。将DO序列分解,所得到的高频与低频序列如图1。


(a) 方差和FPC曲线 (b) AIC和BIC曲线 图2 由DO高频数据所得的方差和各准则函数曲线Fig.2 Variance and standard curves given by DO high frequency data
同理可以得到低频系列的AR模型参数。
最后将高频低频的系列值叠加,得到小波分解高、低频双自回归模型的率定期和预测期的DO过程(图3)。
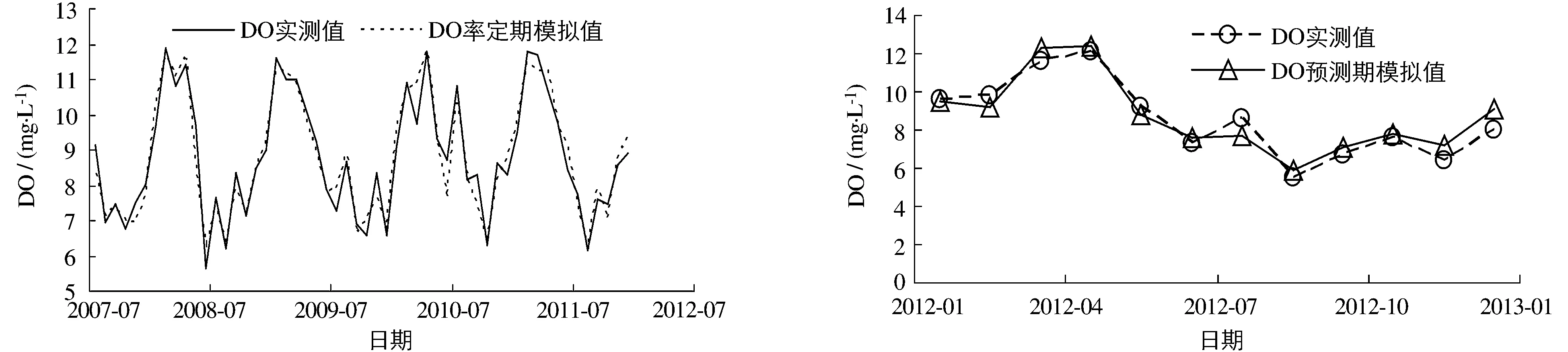
(a) 率定期模拟 (b) 预测期模拟图3 小波分解高、低频双自回归模型模拟DO的率定期和预测期Fig.3 Simulation results of wavelet decomposition high and low frequency double autoregressive model for DO in the period of calibration and predication
由图3可见,小波分解高、低频双自回归模型得到的率定期和预测期模拟效果较好,通过计算其相对误差的平均值可知率定期模拟的平均相对误差为4.23%,预测期的平均相对误差为4.34%。因此,对于DO数据系列,小波分解高、低频双自回归模型得到了令人满意的预测效果。这一模型与单一自回归模型的应用效果对比见表1。

表1 小波分解高、低频双自回归模型与单一自回归模型的应用效果对比Tab.1 Comparison between application effects of the wavelet decomposition of high and
由表1可见,不管是在率定期还是在检验期,小波分解高、低频双自回归模型的模拟精度大大优于单一自回归模型。
4 结 语
从数据序列平稳性角度出发,将多尺度小波分析理论方法与自回归模型相结合,提出了小波分解高、低频双自回归模型的方法,并将其应用于水质预测中。分析结果表明:
(1)小波的多层分解可以过滤出更加精细的数据信号系列,但在建立自回归模型时,各层预测误差会出现叠加现象,为避免多个系列误差的叠加现象,层数不宜过多,一般作一层分解。
(2)不管是在率定期还是在检验期,小波分解高、低频双自回归模型的模拟精度均大大优于单一自回归模型,表明了这一模型的可行性与实用价值。
(3)定期复核,动态优化模型参数。自回归模型基于历史系列进行模型参数的率定,因此,随着历史序列数据的增加,数据样本容量增加,自回归模型的参数宜每隔几年做必要的复核,以动态识别参数,保证模型的适用性及精度,必要时可采用卡尔曼滤波实时校正。由于自回归方法本身的局限性(仅仅从历史数据推测未来的演变情况),当出现突发污染事件的情况下,小波分解高、低频双自回归模型的预测精度可能达不到要求,这时可以结合水库的具体情况,采用卡尔曼滤波进行实时校正,即上面介绍的第4种模型(小波分解+双自回归+卡尔曼滤波)。
参 考 文 献:
[1]黄国如, 芮孝芳. 流域降雨径流时间序列的混沌识别及其预测研究进展[J]. 水科学进展, 2004, 15(2): 255-260. (HUANG Guo-ru, RUI Xiao-fang. Study advances in diagnosis of chaotic behaviour and its prediction for rainfall and streamflow time series in watershed[J]. Advances in Water Science, 2004, 15(2): 255-260. (in Chinese))
[2]翟颢瑾, 高晶. 长江未来水质污染的时间序列分析[J]. 沈阳师范大学学报: 自然科学版, 2006, 24(1): 22-24. (ZHAI Hao-jin, GAO Jing. Time series analysis of future water pollution in Yangtze River[J]. Journal of Shenyang Normal University (Natural Science), 2006, 24(1): 22-24. (in Chinese))
[3]王开章, 刘福胜, 孙鸣. 灰色模型在大武水源地水质预测中的应用[J]. 山东农业大学学报: 自然科学版, 2002, 33(1): 66-71. (WANG Kai-zhang, LIU Fu-sheng, SUN Ming. The application of greymodel in Dawu water quality predication water resource site[J]. Journal of Shandong Agricultural University (Natural Science), 2002, 33(1): 66-71. (in Chinese))
[4]汪万芬, 谭绿贵, 刘晓升. 基于模糊综合评价法的淠河水环境质量评价[J]. 资源开发与市场, 2008, 24(5): 411- 413. (WANG Wan-fen, TAN Lü-gui, LIU Xiao-sheng. Water quality assessment of Pihe River based on fuzzy comprehensive evaluation[J]. Resource Development & Market, 2008, 24(5): 411- 413. (in Chinese))
[5]万金保, 朱邦辉. 物元模型在庐山风景名胜区水环境质量评价中的应用[J]. 安徽农业科学, 2010, 38(6): 3094-3097. (WAN Jin-bao, ZHU Bang-hui. Application of matter element model in water environment quality of Lushan scenic areas[J]. Journal of Anhui Agriculture Science, 2010, 38(6): 3094-3097. (in Chinese))
[6]田建平, 曹东卫, 李海楠. LM-BP神经网络在于桥水库水质预测中的应用[J]. 水利信息化, 2010(3): 31-34. (TIAN Jian-ping, CAO Dong-wei, LI Hai-nan. Application of LM-BP neural network in water quality prediction for Yuqiao reservoir[J]. Water Resources Informatization, 2010(3): 31-34. (in Chinese))
[7]MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693.
[8]徐伟, 何金平. 基于多尺度小波分析的大坝变形自回归预测模型[J]. 武汉大学学报: 工学版[J]. 2012, 45(3): 285-289. (XU Wei, HE Jin-ping. Forecast model of dam deformation based on multi-scale wavelet analysis and autoregressive method[J]. Engineering Journal of Wuhan University: 2012, 45(3): 285-289. (in Chinese))
[9]顾岚, 安鸿志. 自回归模型的精细结构与统计分析[J]. 应用数学学报, 1985, 8(4): 433- 445. (GU Lan, AN Hong-zhi. Statistical analysis of subset AR models[J]. Acta Mathematicae Applicatae Sinica, 1985, 8(4): 433- 445. (in Chinese))

