窄缝坎的冲击波及水舌入水宽度的计算

柳 杨,马 飞,吴建华

(河海大学水利水电学院,江苏 南京 210098)

窄缝坎是收缩式消能工的一种形式,它利用泄水建筑物末端两侧边墙的收缩,使水流经过窄缝坎后形成沿竖向和纵向充分拉伸的挑射水舌,增大水舌在空中的掺气和消能,减轻对下游河床的冲刷。窄缝坎因其高消能率有广泛的应用,特别适用于高窄峡谷的水电工程。我国的龙羊峡、东江、安康、李家峡、天生桥一级、漫湾、水布垭、善泥坡等水电站都采用了窄缝坎的消能方式[1-2]。

明渠边墙偏转会引起冲击波,窄缝坎因其两侧边墙的收缩,改变了流线方向,试验中产生了冲击波。早在1943年,Ippen[3]以力学原理为基础建立了理想冲击波理论,提出了冲击波的基本关系式。Hager等[4-6]通过理论推导得到了冲击波的简化计算式。但是,前期的研究几乎都依赖于静水压力假定,考虑动水压力影响的冲击波研究较少。事实上,窄缝坎后动水压力较大,不再符合静水压力假定,刘亚坤[7]在Ippen关系式中的静水压力项引入了动水压力修正系数,并通过物理模型试验对其进行了率定。宁利中等[8]认为窄缝坎流动条件与明渠收缩段有明显差别,窄缝坎收缩段长度对水流冲击波波角产生一定影响,他们根据模型试验结果给出了计算波角的经验公式。黄智敏等[9]分析认为窄缝坎的波阵线为曲线,冲击波的波角不是一个常数,而是沿程增大的。可见,与明渠相比，窄缝坎偏转角大、水流弗劳德数高,产生的冲击波难以直接用传统冲击波理论进行求解,有必要对窄缝坎冲击波开展进一步的研究。

在消力池的设计中,其结构尺寸根据挑流入池水流的长度和宽度来确定。除了传统挑流水舌运动轨迹的研究[10-12]和水舌横向扩散特性的研究[13-14],吴文平等[15]运用自由抛射体理论研究了窄缝坎挑流水舌的纵向扩散规律,得到了水舌入水的长度。此外,由于窄缝坎内冲击波交汇，在水舌顶部形成水冠,该部分水流在流动过程中从水舌主体两侧散落,决定了水舌入水时的最大宽度。本文通过理论分析和物理模型试验,研究窄缝坎冲击波最大和最小波角;应用冲击波理论和自由抛射体运动原理,建立窄缝坎水舌最大入水宽度及其位置的估算公式,并与模型试验结果进行比较。

1 试验装置与测量参数

试验在河海大学高速水流实验室进行。试验模型系统包括水泵、平水塔、钢板水箱、窄缝坎、尾水渠及回流系统等(图1)。模型试验以某工程泄洪中孔为原型,模型比尺1∶40。该中孔模型采用短有压进口,有压段长64.5 cm,有压段出口顶板设置1∶10压坡,出口断面尺寸为15.0 cm×18.3 cm(宽×高),明渠段长48.3 cm,宽15.0 cm,边墙高38.0 cm,明渠末端为水平底板窄缝坎,底板距下游尾水渠渠底高147.0 cm,两侧边墙宽度由B=15.0 cm收缩至b=8.0 cm。尾水渠中设尾坎以模拟水垫塘,尾坎高67.0 cm,距模型中孔出口723.0 cm。窄缝坎结构参数中,收缩角θ是冲击波波角的主要影响因素,本文研究了收缩角θ分别为17.30°、12.0°和8.0°的情况,相应的模型编号为M1、M2和M3。试验中工作水头为80.0～172.0 cm,来流弗劳德数Fr=2.17～3.85。

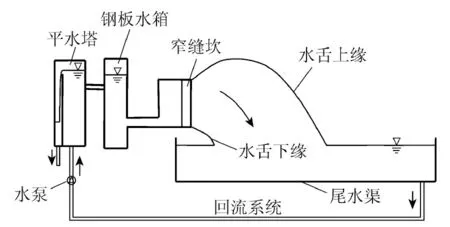
图1 模型试验系统示意图

试验涉及流量、冲击波波角、挑流水舌最大宽度以及最大宽度所在位置等参数，其中,流量采用矩形薄壁堰测量,水舌最大宽度及其相应的位置用钢尺测量,冲击波波角由试验测得的相关参数计算求得。试验中挑射水舌有一定的摆动,相应地，冲击波波角、挑射水舌最大入水宽度及其位置的测量误差约为±5%。

2 流态观察

图2为M1模型窄缝坎水舌形态的试验照片,可以看到,水流进入窄缝坎收缩段后,由于窄缝坎宽度束窄,产生冲击波,水深沿程迅速增大;窄缝坎挑流水舌在纵向和竖向上充分拉伸,水舌与空气接触面积大,掺气充分,整个水舌呈白色;受冲击波影响,水舌顶部形成掺气更为剧烈的水冠,其颜色显得更白些。图3是不同来流条件下M1模型水流俯视照片,可以看出,在冲击波交汇点前,窄缝坎内靠近边墙的水面高于中线水面,即水流表面是从中线到两侧边墙逐渐上升的曲面;窄缝坎冲击波波阵线不是水平的,而是沿流向倾斜向上的;与明渠偏转引起的冲击波不同,随着窄缝坎收缩段内水面逐渐升高,冲击波波阵线不是一条直线,而是一组直线;窄缝坎内靠近两侧边墙的水流形成的波阵线最高,对应波角最小,这两股水流交汇后相互穿越并带着中线上的水流从主体水舌两侧跌落,做近似自由抛物体运动,由于主体水舌厚度较薄,这两股水流入水时所确定的宽度(图2中点A处的横向宽度)即为水舌入水时的最大宽度。试验表明,在所有来流条件下,每组模型都呈现类似的水流流态。

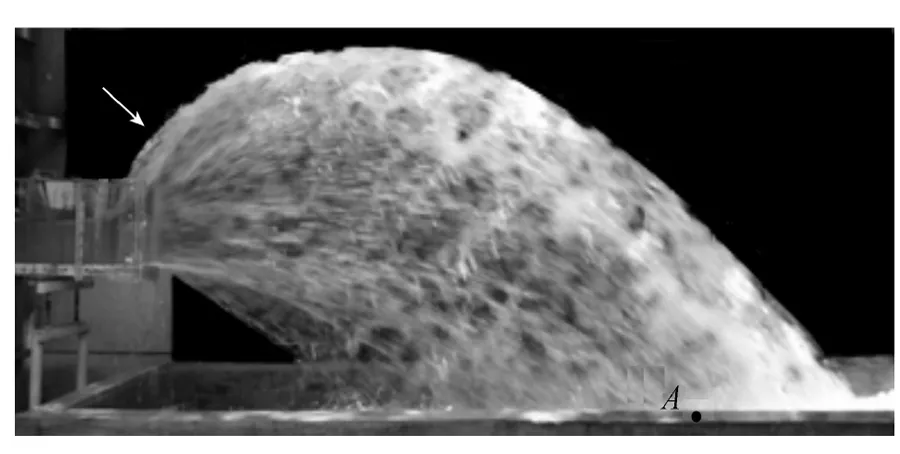
图2 M1模型窄缝坎水舌形态(Fr=3.8)

图3 M1模型水流顶部流态(沿图2中箭头方向拍摄)

3 水舌入水宽度的计算

根据试验现象,绘制了窄缝坎及流态示意图,如图4所示。图中,窄缝进口宽度为B,出口断面宽度为b,收缩段长度为L,收缩角为θ。当水流以速度v1流经收缩段时,产生冲击波,波阵线在水平面的投影和来流方向的夹角为波角,将最大波角记为βM,最小波角记为βm。O′点为冲击波交汇点,从O′点到收缩段起始断面的水平距离定义为L0,O′点水深为h0。

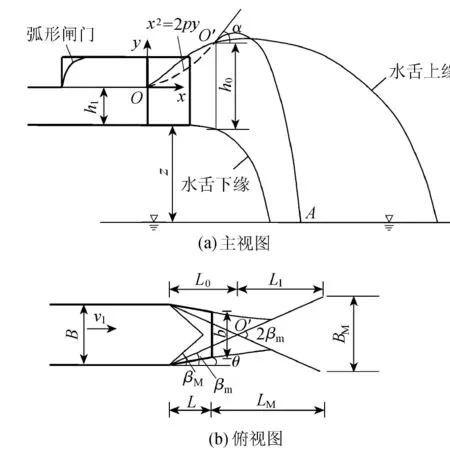
图4 窄缝坎及流态示意图

为方便计算,在图4中建立坐标系xOy。坐标原点O位于收缩段起始处,距离底板高度为h1,x轴为水流方向,y轴竖直向上。窄缝坎底板距下游水面的高度为z,取z=80.0 cm。

如图4所示,在冲击波作用下,窄缝坎收缩段两侧边墙处的两股水流在水舌顶部夹角为2βm。中线上的顶部水流由于剧烈的冲击作用,以最大的出射角α并跟随边墙附近的两股水流从主体水舌两侧跌落,落点为A,则A点处水舌的横向宽度即为窄缝坎水舌最大入水宽度。记此时落点A与冲击波交汇点O′的水平距离为L1,相应的水流落入下游时的水舌宽度,记为BM,即挑流水舌入水时的最大宽度,定义窄缝坎出口距水舌最大入水宽度处的水平距离为LM。则由几何关系可得

(1)

根据式(1)即可求得水舌最大入水宽度BM。在计算时,需要先求解βm和L1。

3.1 波角βM和βm的计算

窄缝坎边墙偏转角较大,冲击波后不再符合静水压力假定,直接用Ippen理论研究窄缝挑坎中的冲击波误差较大,需要进行修正。Hager 等[5]认为,窄缝坎收缩段内形成的冲击波波角可以表示为来流弗劳德数Fr和收缩角θ的函数:

β=f(1/Fr,θ)

(2)

通过分析本文窄缝坎系列模型试验数据,在不同来流弗劳德数条件下分别得到了βM和βm与Fr和θ的关系,如图5和图6所示。

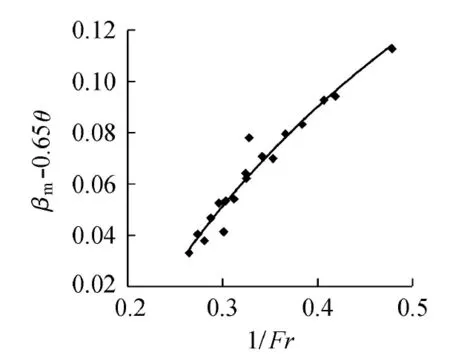
图5 βm-0.65θ与1/Fr的关系

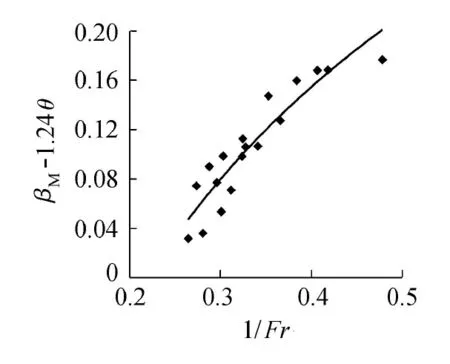
图6 βM-1.24θ与1/Fr的关系

根据式(2),并利用模型试验资料可得

(3)

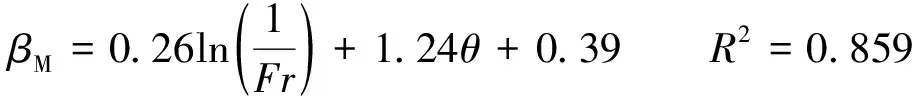
(4)

式(3)(4)的适用范围为:0.139≤θ≤0.302,2.17≤Fr≤3.85。

3.2 L1的近似计算

忽略空气阻力,把挑射水流的运动看作质点的自由抛射体运动,L1可近似按自由抛射体的运动轨迹来计算。根据自由抛射体运动原理可以求得

(5)

式中:v、α分别为冲击波交汇点O′处水流的流速及出射角;h0为交汇点O′处水深。确定了v、α及h0后,可得到L1的值。

3.2.1 v的求解

Ippen冲击波理论给出了冲击波波后水流流速:

(6)

由式(6)可知,当来流流速及收缩角一定时,波后流速的大小取决于波角。经试算,近似以水冲击波波角βM的值代入式(6),计算冲击波波后水流流速,即

(7)

3.2.2 h0的求解

为了求解h0,列来流断面和O′断面的连续性方程,并以O′点的流速v代表O′断面的平均流速。由于O′点距离窄缝坎出口很近,该断面处水舌横向收缩和底部向下扩散很小,因此,将O′断面近似认为是宽B0、高h0的矩形断面,则

v1h1B=vh0B0

(8)

式中:v1和h1分别为来流断面流动的平均流速和水深;B0为O′断面处水流宽度,并且近似B0≈b,则由式(8)可得

(9)

3.2.3 α的求解

在xOy坐标系中(图4),求解冲击波交汇点处的水流出射角α,图中虚线为窄缝坎中线截面上的水面线,可用抛物线函数x2=2py近似表达[16]。在出射角α的计算中,近似以水深h0代替O′点到出口底板的高度,O点坐标(0,0),O′点坐标为(L0,h0-h1),则p=L02/(2(h0-h1),进而得到抛物线方程为x2=L02y/(h0-h1)。对方程在O′点求导，得该点的斜率tanα=2(h0-h1)/L0,因此,出射角α可以近似表示为

(10)

将式(7)(9)(10)代入式(5),可以计算得出L1的值。最后,将式(3)和(5)代入式(1),可得到窄缝坎挑流水舌最大入水宽度BM及最大宽度位置LM。

4 试验验证

采用河海大学高速水流实验室窄缝坎模型试验系统来验证上述计算过程，其中窄缝坎来流流量已知,h1可近似等于有压段出口高度18.3 cm,根据流量-水位关系和结构参数,可得到来流流速v1及水流弗劳德数Fr。利用本文的计算方法求得水舌最大入水宽度BM和窄缝坎出口距水舌最大入水宽度处的水平距离LM，在模型试验中测量每种工况下的BM以及LM，将BM和LM的计算值及实测值点绘在图7和图8中，可以看出,两者吻合较好，表明本文计算方法理论基础可靠，计算过程简便，具有较高的精度。

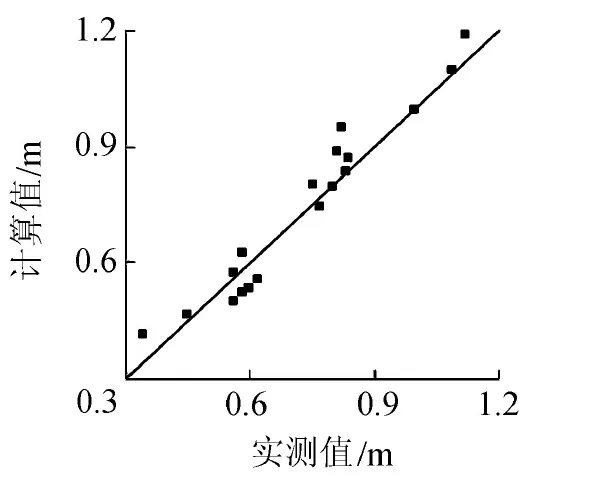
图7 BM实测值与计算值的比较

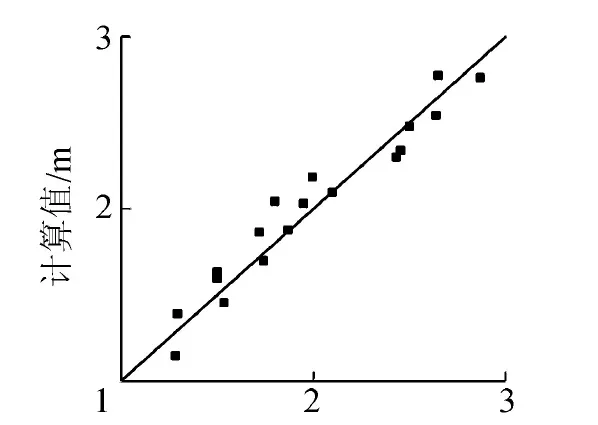
图8 LM实测值与计算值的比较

5 结 语

窄缝坎是一种常用的水力消能单元,试验表明,通过窄缝坎的流动受冲击波的作用,在其收缩段表面产生多条倾斜向上的波阵线,对应着不同的波角,根据本文试验结果得到,波角随来流弗劳德数的减小及窄缝坎收缩角的增大而增大。水舌顶部的冲击波交汇后分成左右两股水流向下游跌落,决定了水舌的最大入水宽度。试验研究表明,随着收缩角或来流弗劳德数的增大,窄缝坎挑射水舌最大入水宽度增大且其位置向下游偏移。本文通过理论分析和试验研究,得到了窄缝坎挑射水舌最大入水宽度及其所在位置的估算公式。经与模型试验结果比较,两者吻合情况较好，表明本文计算方法具有较高的精度。

参考文献：

[1] WU Jianhua,MA Fei,YAO Li.Hydraulic characteristics of slit-type energy dissipaters [J].Journal of Hydrodynamics,2012,24(6):883-887.

[2] 黄秋君,吴建华.收缩式消能工的研究现状及进展[J].河海大学学报:自然科学版,2008,36(2):219-223.(HUANG Qiujun,WU Jianhua.Research on contraction energy dissipators [J].Journal of Hohai University:Natural Sciences,2008,36(2):219-223.(in Chinese)

[3] IPPEN A T.Gas-wave analogies in open channel flow [C]//Proceedings of the Second Hydraulics Conference.Iowa:University of Iowa,1943:248-265.

[4] HAGER W H.Supercritical flow in channel junctions [J].Journal of Hydraulic Engineering,1989,115(5):595-616.

[5] HAGER W H,SCHWALT M,JIMENEZ O,et al.Supercritical flow near an abrupt wall deflection [J].Journal of Hydraulic Research,1994,32(1):103-118.

[6] NI Hangen,LIU Yakun.A generalized explicit solution of the sequent depth ratio for the hydraulic jump [J].Journal of Hydrodynamics,2005,17(5):596-600.

[7] 刘亚坤.冲击波与收缩式消能工若干问题的研究[D].大连:大连理工大学,2006.

[8] 宁利中,戴振霖.窄缝挑坎收缩段急流冲击波及控制水深的计算[J].西安理工大学学报,1992,8(3):197-240,215.(NING Lizhong,DAI zhenlin.Calculations of shock waves and controlling water depth in region of contraction on slit-type flip bucket [J].Journal of Xi’an University of Technology,1992,8(3):197-240.(in Chinese)

[9] 黄智敏,翁情达.窄缝挑坎收缩段急流冲击波特性的探讨[J].水利水电技术,1989(8):11-15.(HUANG Zhimin,WENG Qingda.Discussions on characteristics of shock waves on slit-type flip bucket [J].Water Resources and Hydropower Engineering,1989(8):11-15.(in Chinese)

[10] 刘宣烈,张文周.空气阻力对挑流水舌的影响[J].天津大学学报,1982(2):67-77.(LIU Xuanlie,ZHANG Wenzhou.Effect of air resistance to a trajectory jet [J].Journal of Tianjin University,1982(2):67-77.(in Chinese)

[11] 刘宣烈,刘钧,姚仲达,等.空中掺气水舌运动轨迹及射距[J].天津大学学报,1989(2):23-30.(LIU Xuanlie,LIU Jun,YAO Zhongda,et al.The moving orbit and the horizontal length of aerated jet flow in open air [J].Journal of Tianjin University,1989(2):23-30.(in Chinese)

[12] 宁利中.挑流水舌挑距及其影响因素概述[J].水资源与水工程学报,2004,15(3):35-39.(NING Lizhong.Discussion on the horizontal length of jet flow and its factors of influence [J].Journal of Water Resources & Water Engineering,2004,15(3):35-39.(in Chinese)

[13] 刘宣烈,刘钧.三元空中水舌掺气扩散的试验研究[J].水利学报,1989,17(11):10-17.(LIU Xuanlie,LIU Jun.Experimental study on the diffusion and aeration of three-dimensional jet [J].Journal of Hydraulic Engineering,1989,17(11):10-17.(in Chinese)

[14] 傅佩芬.溢流拱坝挑流水舌入水宽度计算[J].四川水力发电,2000,19(增刊1):70-71.(FU Peifen.The calculation of the jet width of overflow arch dams [J].Sichuan Hydropower,2000,19(Sup1):70-71.(in Chinese)

[15] 吴文平,张彦法.窄缝挑流水舌的运动扩散规律及应用[J].水力发电学报,1989(4):71-76.(WU Wenping,ZHANG Yanfa.The theory and appliance of jet diffusion for slit-type flip bucket [J].Journal of Hydroelectric Engineering,1989(4):71-76.(in Chinese)

[16] 张叶林,邓军,刘军,等.丹达河水电站窄缝消能研究[J].人民黄河,2011,33(6):126-131.(ZHANG Yelin,DENG Jun,LIU Jun,et al.Research on slit-type energy dissipaters of Dandahe Hydropower Station [J].Yellow River,2011,33(6):126-131.(in Chinese)