基于类Frank码的非连续LFM距离旁瓣抑制*

沈佳琪，桂任舟

(同济大学电子与信息工程学院，上海200092)

目前，由于3G、LTE乃至LTE-A等通信系统的用户数量不断增加，自由空间中可利用的连续“寂静”频段越来越少，而零星频率段则较多。但是，为了减小雷达系统目标检测的距离及速度模糊，提高通信系统的有效性，增强某些应用的性能[1-2]，系统发射的波形需要具有较大的带宽[3]。因此，国内外的学者们都致力于如何充分利用现有的自由空间资源，提高发射信号的带宽。

[4-5]提出了针对高速及高机动情况下频率步进信号的宽带模糊函数，证明了通过宽带模糊函数可以得知高速运动目标对于时延及多普勒影响。GREEN S和KINGSLEY S提出了非连续频谱线性调频信号DS-LFM(Discontinuous Spectra Linear Frequency Modulation)[6]。针对频谱不连续造成的旁瓣，用回波信号估计谱对回波信号进行补偿。在得到准确估计的情况下，该方法能够压低距离旁瓣，但是其适用的频率范围相对较小。此后，参考文献[7-10]利用回波信号的相位以及内插-外推算法、CLEAN算法有效地提取了速度及距离信息，压低了距离、速度旁瓣。但是，这些方法还是存在一些不足，例如适用的载频变化范围小、所需计算量大等。

经过对Frank码特性的研究，从Frank码中抽取一部分码元，并且根据实际应用情况进行扩展，提出了一种类Frank码的码型。运用该码型对DS-LFM信号相位进行控制，可以减小或消除由于载波频率不连续导致的回波信号的相位跳变，提高模糊函数的测量精度。

1 类Frank码的提出

1.1 接收端基带信号的相位跳变问题

DS-LFM发射信号可表示为[8]：

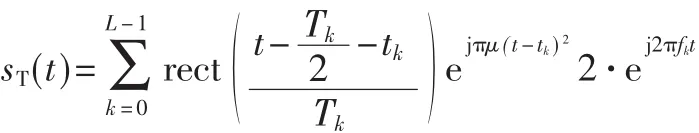
其回波信号为：

其中τ为时延。

将接收到的回波信号进行混频及低通滤波处理后得到的基带信号如式(1)所示：

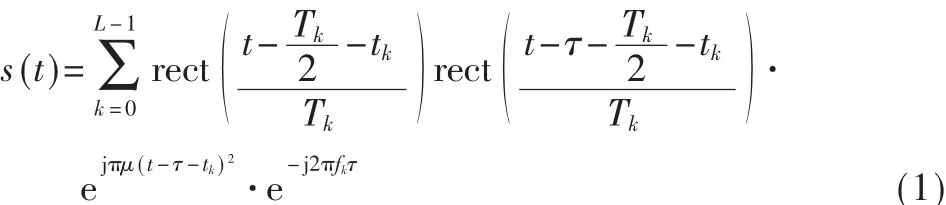
接收端基带信号上任意两点的相位差为：

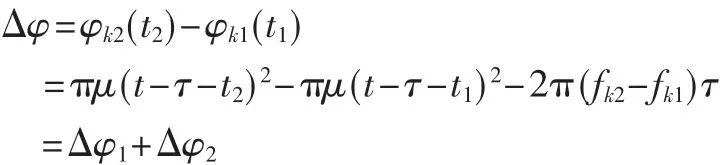
其中Δφ1=πμ(t-τ-t2)2-πμ(t-τ-t1)2,Δφ2=-2π(fk2-fk1)τ。若两段的载频分别为f1与f2，且忽略连续的相位变化值Δφ1，可得此时的相位差为：

所以，非连续谱LFM信号的相位跳变主要由载波频率的变化引起，其在载频跳变点处的值为2πΔfτ，其中Δf=f1-f2。该跳变会引起匹配滤波后的高距离旁瓣，在模糊函数中则表现为大的距离模糊。

1.2 类Frank码

类Frank码的推导过程如下。

周期为N=q2的Frank序列集可表示为[11]：

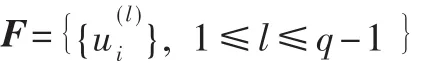
其中，m为行数，n为列数。其第r行的相位值为Δφr,n=

2 调制有类Frank码相位的DS-LFM波形

调制有类Frank码相位的DS-LFM信号的发射波形为：

其中φ(t)为类Frank码。经过混频及低通滤波处理后得到的基带信号为：

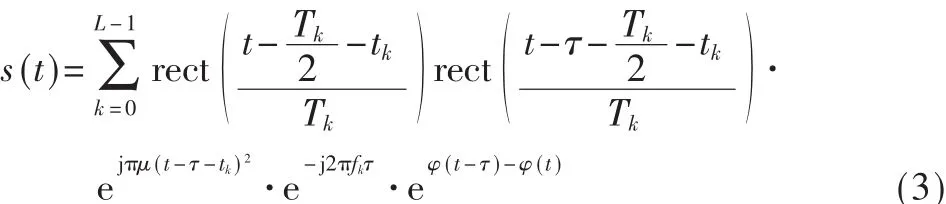
若忽略连续的段间相位变化，则该信号的相位差为：

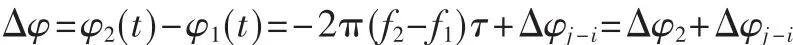
其中，Δφj-i即为类Frank码的差序列之差。若取适当的Δφj-i，使得-Δφj-i=Δφ2成立,则相位跳变Δφ即可被抵消，非连续谱LFM信号的模糊函数性能即可得到改善。

3 仿真结果与分析

本文分别对载波频率数为5的情况进行了仿真。仿真中采样频率设置为480 kHz,5段子信号的初始频率分别为1MHz、1.001MHz、1.002 MHz、1.003 MHz和1.004 MHz。目标距离设定为7.5 km，发射波形的带宽为120 kHz,脉冲宽度为2.5 ms。选用的类Frank码的阶数为20,时延参数p选为24,从类Frank矩阵中选取第1、3、5、7、9行组成类Frank码。

图1为载波数为5时，接收端回波基带信号在第4段与第5段信号跳变处的相位图。从该图中可以观察到，原本较大的相位跳变在补偿之后接近于连续频谱LFM信号的相位。模糊图沿距离轴切割(图2)的对比表明，旁瓣峰值由原来非连续频谱的40%降到了20%。

图1 载频数为5的接收基带信号在第四处相位跳变图

如图2所示,通过对载频数为5时的仿真可以看出，该方法可以有效地补偿DS-LFM信号在接收端的基带信号相位跳变，由该方法得到的信号的模糊函数有较好的特性，其距离模糊问题得到了解决。

为了增加线性调频信号的带宽而采用的非连续频谱信号的方法可以充分利用自由空间中的零散频段，但是由此而产生的信号相位不连续问题致使距离旁瓣增大。本文提出了一种类Frank码型，该码型由Frank码扩展抽取而来。利用该码型控制发射DS-LFM波形的相位可以改善接收基带信号的相位不连续问题。本文通过理论推导及仿真分析证明了该方法的可行性。

参考文献

[1]单慧琳,张银胜,唐慧强,等.对称三角线性调频连续波雷达应用于风速探测[J].电子技术应用,2013,39(1):119-121,124.

[2]桂任舟.利用二维恒虚警进行非均匀噪声背景下的目标检测[J].武汉大学学报：信息科学版,2012,37(3):354-357.

图2 载频数为5时DS-LFM信号模糊函数的切割

[3]Liu Guosui,Gu Hong,Zhu Xiaohua,et al.The present and the future of random signal radars[J].IEEE Aerospace and Electronic Systems Magazine,1997,12(10):35-40.

[4]李磊,任丽香,毛二可,等.频率步进信号宽带模糊函数及其应用[J].北京理工大学学报,2011,31(7):844-848.

[5]Zhu Yongfeng,Zhao Hongzhong.Wideband joint rangevelocity-acceleration ambiguity function of stepped frequency signal[J].IET International Conference on Radar Systems,2012,1(5):22-25.

[6]GREEN S D,KINGSLEY S P.Improving the range/time sidelobes of large bandwidth discontinuous spectra HF radar waveforms[J].Seventh International Conference on HF Radio Systems and Techniques,1997，7(7-10):246-250.

[7]Zhang Dongpo,Liu Xingzhao.Signal processing technique for randomly discontinuous spectra HF radar waveforms[J].Journal of Systems Engineering and Electronics,2004,15(4):511,515.

[8]熊俊志,杨子杰,周辉林,等.非连续谱FMCW雷达信号分析与处理[J].电波科学学报,2006,21(3):377-381.

[9]熊俊志,杨子杰,王勤,等.基于内插/外推的非连续谱高频雷达二维处理[J].电波科学学报,2006,21(5):735-739.

[10]王勤,万显荣,杨子杰,等.基于CLEAN算法的非连续谱线性调频中断波信号处理[J].电波科学学报,2009,24(2):243-248.

[11]朱晓华.雷达信号分析与处理[M].北京:国防工业出版社,2011.