大侧滑模型参考自适应飞行控制方法研究

程鹏飞，吴成富，冯成，郭月

(1.西北工业大学无人机特种技术重点实验室，陕西西安710065；2.西北工业大学自动化学院，陕西西安710072)

如今新一代高可靠容错飞行控制战斗机、大型客机、大型运输机、高空长航时无人机均采用新一代电传飞行控制系统。为了提高飞机的生存能力，高可靠容错飞行控制理论和技术得到了世界各国的重视。美国Rockwell Collins公司先后完成了单侧机翼突然折损40%、60%、80%面积矩后的试飞验证[1]；美国Gatach大学实现了容忍单侧机翼断掉50%面积矩的试飞验证[2]。国内部分院校的学者也进行了无故障或舵机卡死等故障下自适应飞行控制算法的研究[3-6]。然而大多数研究都只是单独针对纵向、侧向，甚至是单一传递函数进行自适应控制算法研究，对于故障前后配平点变化问题也没有给出分析和解决方法，缺乏通用性和适用性。为了解决上述问题，本文综合纵/侧向通道，设计了适用于无故障、单侧副翼舵机卡死故障、单侧机翼严重损伤下大侧滑角飞行的模型参考自适应飞行控制系统，并进行了多种情况下的数字仿真。从仿真结果可以看出该控制系统具有较好的系统性和实用性。

1 大侧滑角飞行控制方案

当飞机在飞行过程中突然出现单侧副翼舵机卡死或者机翼部分损伤时，只靠偏转另一侧副翼来提供恢复力矩是不够的，所以必须改变控制策略，通过调整飞行姿态，给出侧滑角来尽可能提供更多的恢复力矩。大侧滑角飞行控制系统如图1所示。

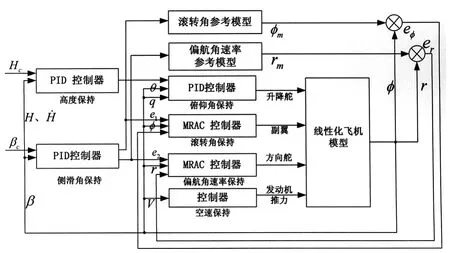
图1 大侧滑角飞行控制方案

控制结构方面，此控制方案由内环姿态角控制器和外环高度保持(Height Hold)、侧滑角保持(Sideslip Angle Hold)控制器级联组成。侧向通道中，侧滑角保持控制器的输入信号βc通过PID控制器滤波后，作为滚转角保持(Roll Angle Hold)和偏航角速率保持(Yaw rate Hold)控制器的给定，并分别将各自输出信号送给副翼(da)和方向舵(dr)，用来分别调节滚转角和偏航角速率最终跟踪βc。纵向通道的高度保持器将偏差信号送入俯仰角保持(Pitch Angle Hold）器中，继而调节升降舵(de)跟踪Hc。这种两极控制结构不仅能够使飞机大侧滑角飞行，而且能够在此基础上直线飞行，有利于航路点绕飞。控制算法方面，由于大侧滑机动过程或单侧副翼舵机卡死故障下的侧向传递函数都会发生分子分母系数不确定和变化的现象，所以需要对副翼—滚转角通道(da→φ)和方向舵—偏航角速率通道(da→r)进行MRAC设计来适应不确定性。外环级联的侧滑角控制器和纵向控制器均采用PID控制算法实现。下面重点对图1中两个MRAC控制器结构和算法进行研究。

2 MRAC控制结构和算法设计

2.1 控制结构

本文采用直接模型参考自适应结构进行设计[7]。其特点是不单独对控制器参数进行辨识[8]，而直接对输出误差e=y-ym进行跟踪设计。MRAC控制器的输入r，连同其输出y、ym和内部滤波信号一起构成控制律和自适应律，从而跟踪参考模型的输出。图2给出了dr→r通道的MRAC结构图，da→φ通道类似。

2.2 控制律设计

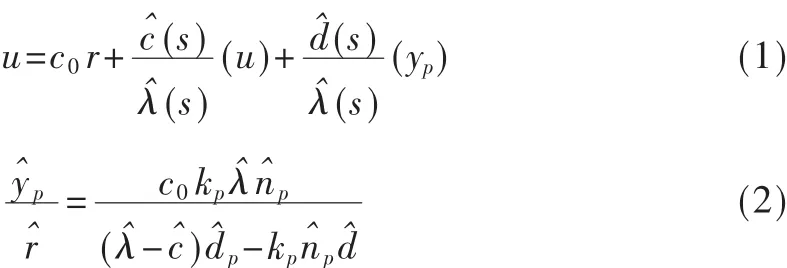
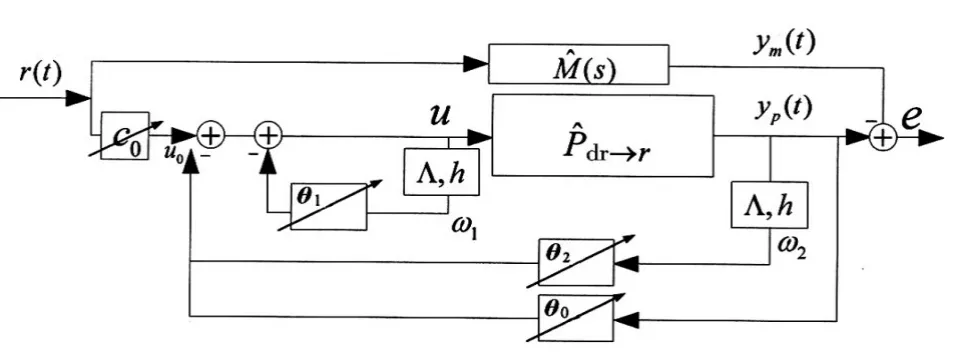
首先选取一个标称被控对象的配平工作点，经过小扰动线性化后得到相对阶为1的被控对象传递函数。前馈部分和反馈部分的滤波器分别将被控对象传递函数的零极点配置成模型的零极点，了使跟踪误差e渐进收敛为零，需要系统地对控制器的参数θ1T、θ2T、θ0进行自适应律设计。

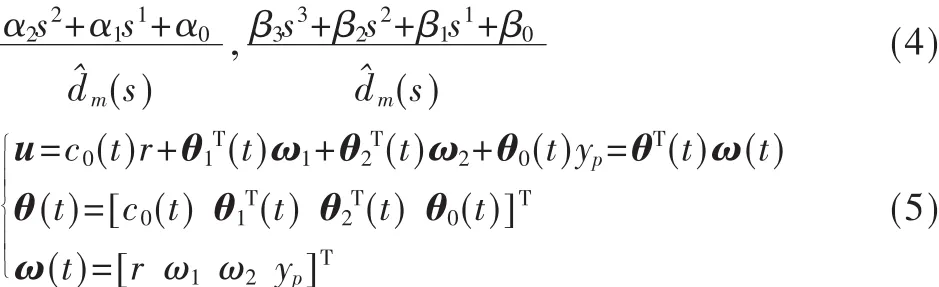
2.3 自适应律设计

记参数误差为f(t)=θ(t)-θ*，首先需要找到跟踪误差和参数误差之间的联系。利用一点简单的技巧,得到e(t)与f(t)之间的关系，如式(6)：

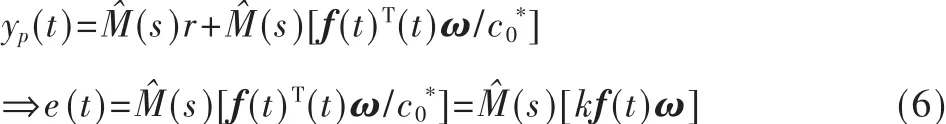
将式(6)写成状态空间的形式。假设M^(s)为严正实，由MKY定理得知，对给定的正定矩阵Q，存在正定矩阵P使得式(8)成立。

取正定函数V如式(9)，求导数如式(10)。

因此，系统是全局有界，即e和f全局有界。进一步，假设r(t)有界，由滤波信号ω1、ω2和yp的有界性得知递归量ω(t)有界，则由式(6)知x˙也有界，故V¨=-2xQx˙有界，此意味着V˙一致连续。由Barbalat引理得到e(t)→0。进一步，由e可知f˙∈L2∩L∞(Lp为p范数)，再加之f∈L∞，则有f˙→0。在f˙→0基础上，倘若ω(t)是持续激励信号，则控制参数误差f→0，并能反向进行飞机参数辨识[9-10]。

3 仿真结果

本节选取某小型电动无人机(常规V尾布局，翼展1.9 m，机长1.95 m，缩写为SEPUAV)来搭建大侧滑角模型参考自适应飞行控制系统仿真模型。在设定的仿真条件下，针对无故障和右副翼舵机卡死故障给出大侧滑角模型参考自适应控制器的非线性数字仿真结果并进行分析。

3.1 无故障、气动数据摄动50%

气动数据摄动用作检验控制器的鲁棒性。将无故障、无气动摄动下设计的大侧滑角模型参考自适应飞行控制器参数初值θ(t)全部设置为零。然后在某一时刻接入摄动后的模型中，观察跟踪βc=-9°的状态响应和参数变化情况，如图3所示。图3(a)～(d)为侧滑角β、飞行高度H、副翼adef、方向舵-偏航角速θ0(t)]T第4分量的响应曲线。可以看出，在大侧滑角MRAC控制系统的作用下，尽管控制器参数初值任意选取，并且摄动高达50%，但β依然能无静差地跟踪指令，高度保持工作正常。另外，3个舵偏量的峰值全部保持在有效舵偏内。因为有θ˙(t)→0，虽然参数θ0(t)在20 s内单调下降，但最终稳定。

3.2 右副翼舵机上偏卡死20°

当故障检测定位不是很精确时，利用故障前的配平点进行故障后控制器的设计至关重要。图4、图5分别为无气动摄动和50%摄动下，出现右副翼舵机上偏卡死20°故障时，跟踪-9°侧滑角令的部分输出响应和自适应控制器参数的变化情况。各子图代表的状态量与图3情况一样。在响应起初的20 s内，图4(a)β基本达到无偏差稳定，而图5(a)则仍旧在-9°附近衰减震荡。相比图3、图4,图5的舵偏调节中出现一些高频震荡成分，而在气动摄动影响下，图5暂态部分的震荡时间相比图4更长。控制器参数的稳定性与3.1节的情况一样，只是震荡加剧稳定时间更长。

图3 气动摄动50%时的飞行状态和控制参数响应

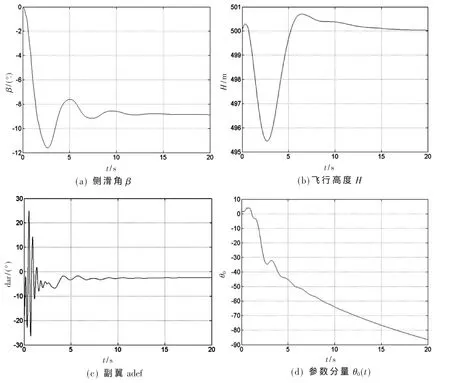
图4 右副翼舵机卡死时的状态和控制参数响应(无气动摄动)

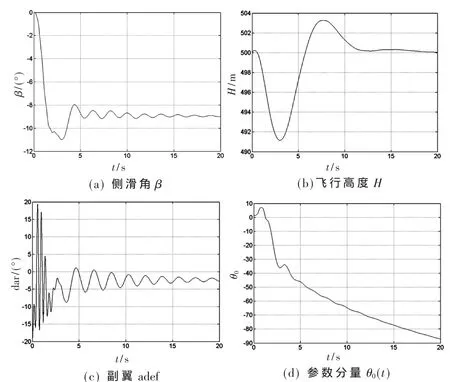
图5 右副翼舵机卡死时的状态和控制参数响应(气动摄动50%)

综上所述，大侧滑角飞行控制器不仅能够利用故障前的配平值在副翼舵机卡死和控制参数初值任选下无静差跟踪侧滑角指令，而且在较大气动数据摄动情况下具有鲁棒性，体现出良好的实用性和通用性。

本文给出了基于模型参考自适应算法的大侧滑角飞行控制系统方案解决无人机副翼舵机卡死故障的控制问题。在保证副翼—滚转角通道和方向舵—偏航角速率通道自适应无静差跟踪模型的基础上，实现了侧滑角指令的无静差跟踪以及高度、速度保持功能。仿真结果表明，此控制系统在控制参数值任给和单侧舵机卡死故障的情况下能够鲁棒地使飞机准确跟踪侧滑角指令，实现上述情况下的大侧滑角直线飞行。后续将对自适应控制器参数的指数收敛性进行研究，并将间接模型参考自适应算法结合进来。

[1]JOURDAN D B,PIEDMONTE M D,GAVRILETS V，et al.Enhancing UAV survivability through damage[C].AIAA Guidance,Navigation,and Control Conference,2-5 August 2010,Toronto,Ontario Canada.

[2]JOHNSON E N,CHOWDHARY G V,KIMBRELL M S.Guidance and control of an airplane under severe structural damage[C].AIAA Infotech@Aerospace 2010,20-22 April 2010,Atlanta.

[3]郑祥明,昂海松,黄达.飞翼式微型飞行器飞行动力学特性研究[J].航空学报,2006,27(3):374-379.

[4]齐晓慧,杨志军,吴晓蓓.基于简单自适应控制的鲁棒飞行控制律设计[J].电光与控制,2010,17(5):6-9.

[5]王首斌，王新民，李俨.模型参考自适应电传飞行控制系统纵向控制律设计[J].火力与指挥控制,2012,37(3):158-164.

[6]董文瀚,孙秀霞,林岩，等.一类直接模型参考Backstepping自适应控制[J].控制与决策，2008,23(9):981-986.

[7]KUTAY A T,CHOWDHARY G,ANTHONY J,et al.A comparison of two novel direct adaptive control methods under actuator failure accommodation[C].AIAA Guidance,Navigation and Control Conference and Exhibit,18-21,August 2008,Honolulu,Hawaii.

[8]DEBUSK W M,CHOWDHARY G,JOHNSON E N.Realtime system identification of a small multiengine aircraft[C].AIAA Atmospheric Flight Mechanics Conference,10-13 August 2009,Chicago,Illinois.

[9]JOHNSON E N,CALISE A J,TURBE M A.Fault tolerance through direct adaptive control using neural networks[].AIAA Guidance,Navigation,and Control Conference and Exhibit,21-24 August 2006,Keystone,Colorado.

[10]刘少华,段征宇.飞行器自适应控制参考模型建立方法研究[J].飞行力学,2011,29(4):56-59.