单孔锚具锥角搭配对其承载性能的影响

刘建月，崔小朝

(太原科技大学 应用科学学院， 山西 太原 030024)

锚索支护结构通过将足够长的锚索深入到较稳定的岩层中并施加预应力来使岩体稳固[1-4]。单孔夹片式锚索支护系统广泛应用于煤矿的巷道支护，对煤炭安全生产起着重要作用。夹片式锚具由锚环和夹片组成，是该支护系统中的核心部件，其承载能力直接影响到支护结构的安全。

影响锚具承载能力的因素很多[5-7]，夹片和锚环在受载下有非常复杂的力学行为，因此，使用有限元软件对夹片式锚具进行数值模拟是当前分析锚具的主要方法。目前，对夹片式锚具的分析主要侧重于夹片和锚环间的摩擦系数和锚具材料对其性能的影响[8]。

本文考虑锚环和夹片不同的锥角搭配对锚具承载能力的影响。以非线性有限元分析软件ABAQUS为平台，建立22组锚环和夹片不同角度搭配的有限元模型，对计算结果的分析发现，合理搭配锚环和夹片锥角能有效提高锚具的承载能力，为锚具的生产和研制提供参考。

1 夹片式锚具的工作原理

锚具正常工作时，夹片咬紧钢绞线，随着岩体的移动夹片在锚环中滑动自锚(见图1)。

忽略锚具材料变形，锚具有效自锚的条件是夹片与钢绞线之间摩擦角α、锚环与夹片摩擦角γ、锚具锥角β需满足以下条件[9]：

tanα≥ tan(β+γ)

式中角度均为弧度制，且锚环与夹片具有相同的锥角β。

考虑到材料变形，因材料轴向不均匀分布，夹片在锚环中滑动锁紧的过程中，会在刚度大难变形的区域产生应力集中，当前广泛生产使用的锚具夹片与锚环锥角相同，不均匀的应力分布影响了锚具的承载能力。

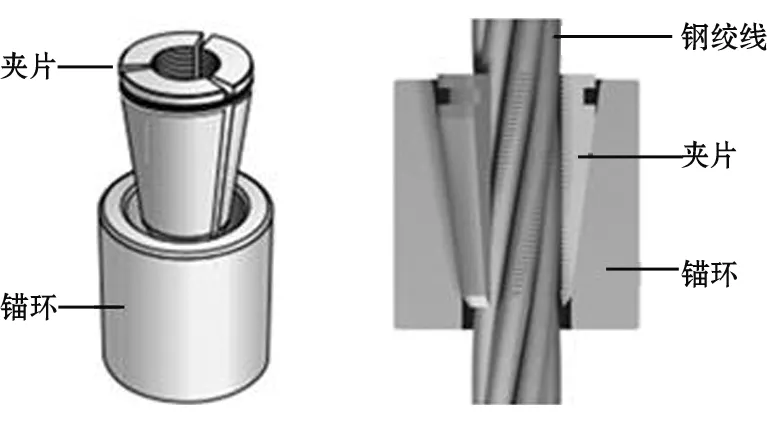
图1 锚具工作原理

2 计算模型

2.1 几何模型

钢绞线和夹片的接触不作为本文研究的重点，将钢绞线和锚环视为整体，参考30 t矿用单孔锚具尺寸，轴对称几何模型简化为图2，长度单位为毫米(mm)，角度单位为度(°)。

β1与β2分别为相互搭配的锚环锥角和夹片锥角，模型中保持β2为7°，β1从6°～8°以0.1°为增量，建立22个有限元计算模型，其它尺寸保持不变。

2.2 材料参数

为更真实反映锚具受载时的力学行为，给模型赋予试验测得的非线性的材料属性，允许模型产生塑性变形。材料参数见表1。

2.3 单元与边界条件

为防止计算过程中因材料塑性变形产生体积自锁，选取的CAX4I单元(4节点四边形双线性非协调轴对称单元)，单元尺寸约为2 mm。锚具共划分567个单元，2268个积分点和2268个单元节点，计算模型的有限元网格如图3所示。

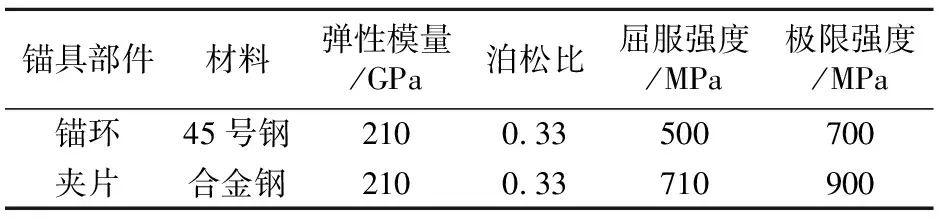
锚具部件材料弹性模量/GPa泊松比屈服强度/MPa极限强度/MPa锚环45号钢2100.33500700夹片合金钢2100.33710900

图3 计算模型的轴对称有限元网格

模型中将夹片锥面设为主面，锚环锥面设为从面，接触属性为硬接触，摩擦系数设为0.02，接触面间滑移量设为有限滑移[10](finite sliding),允许接触面发生较大滑动，位置误差限设为0.01 mm即两个接触面间的距离小于0.01 mm时，ABAQUS自动识别两个面接触[11-13]。约束锚环底面轴向位移，约束夹片顶面径向位移和对称面内的转动，夹片施加轴向大小为30 t的载荷。使用Newton-Raphson算法提交ABAQUS/Standard求解。

3 计算结果

分别对22组计算结果进行后处理，得到锚具在30 t载荷作用下的Mises应力[14]云图(见图4～图7)。

从图4～图7可看出，保持夹片7°锥角不变，随着锚环角度的增加，应力集中区域从锚环入口处向出口处转变。锚环锥角为6°时，锚环入口与夹片接触的区域出现严重的应力集中(见图4)。应力集中区域因应力水平达到强度极限而破坏。

图4 锚环6°，夹片7°

随着锚环锥角的增加，锚环与夹片接触面上的应力分布趋于均匀，当锚环锥角增大到6.5°时，锚环接触面附近应力相对均匀，夹片整体未现严重的应力集中(见图5)。

图5 锚环6.5°，夹片7°

当锚环锥角继续增大时，锚环出口处与夹片接触的区域出现明显的应力集中，夹片端部应力水平急剧增加(见图6、图7)。

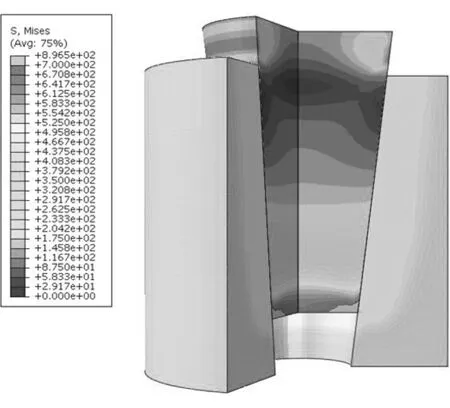
图6 锚环7°夹片7°

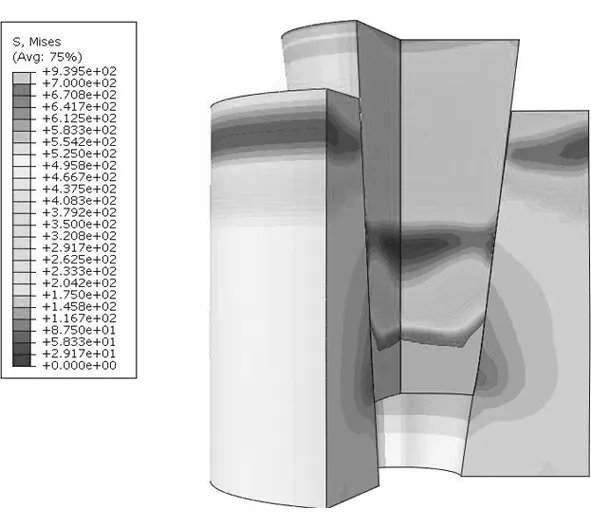
图7 锚环8°，夹片7°

为说明不同锚环、夹片锥角组合对应的锚具应力水平，对每组计算模型锚环288个单元的1152个积分点、夹片279个单元的1116个积分点、锚环锥面和夹片锥面各128个节点分别提取Mises应力值。对得到的值分别进行平均、求最大值和标准差。得到锚具在30 t载荷下锚环、夹片和两个接触面上Mises应力的最大值、平均值和标准差随锚环角度增加的变化趋势(见图8～图10)。

锚环与夹片Mises应力最大值随锚环锥角的增大均呈现出先减小后增大的趋势，锚环在7°附近出现极小值，夹片在6.8°附近出现极小值，但随着锚环锥角的继续增加，夹片应力最大值迅速在增大，甚至超过强度极限而破坏(见图8)。

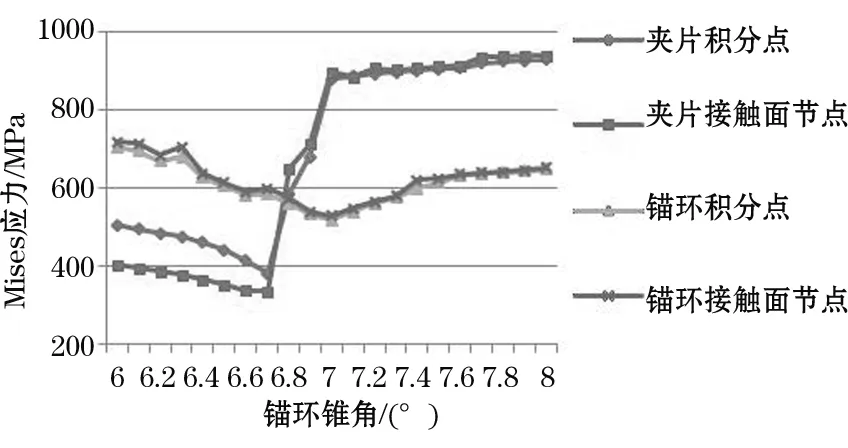
图8 Mises应力最大值随锚环锥度变化

锚环与夹片的Mises应力平均值随锚环角度的增加变化较为平稳，且在7.1°附近出现极小(见图9)。

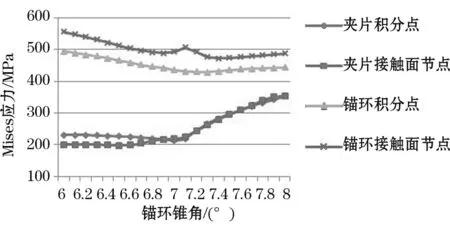
图9 Mises应力平均值随锚环锥度变化

以应力标准差反应锚具受载时应力分布的不均匀程度。随着锚环锥角的增大，夹片与锚环标准差均呈现出先减小后增大的趋势(见图10)。夹片在锚环锥角6.7°附近出现极小值，说明此时夹片的应力分布最均匀；而锚环应力分布最均匀时，锚环的锥角约为7.1°。

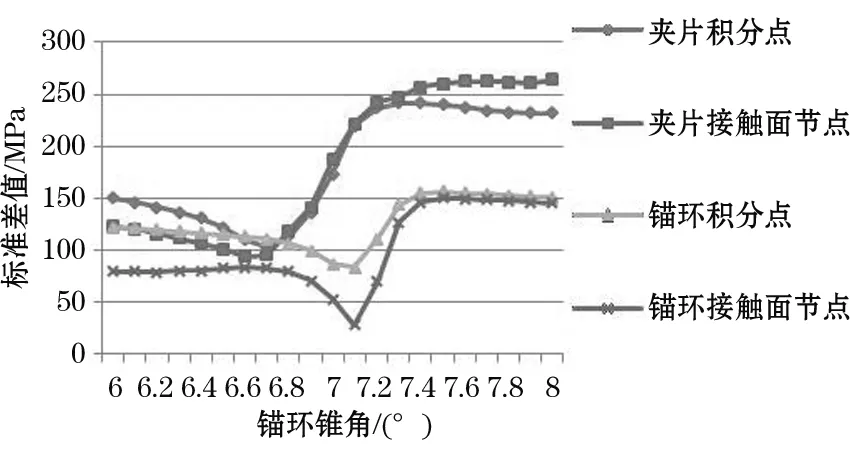
图10 Mises应力标准值随锚环锥度变化

综合考虑夹片和锚环的应力状态，当夹片锥角为7°时，锚环锥角在6.5°～6.8°是比较合理的。在此基础上，对锚环锥角6.3°～7.3°的模型进行连续加载模拟，以锚环和夹片各自的材料强度极限为依据，得到锚环锥角变化时，锚具的承载极限(见图11)。夹片锥角7°，锚环锥角为6.5°～6.8°时，锚具的承载极限比夹片与锥角同为7°时可提高2.6%～4%。

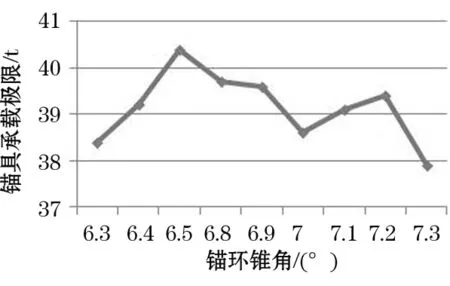
图11 锚具承载极限随锚具角度变化

4 结 论

(1) 应用有限元分析软件ABAQUS对单孔夹片式锚具进行材料非线性和边界条件非线性分析，得到了锚具夹片和锚环在受载下的应力状态云图。

(2) 对结果的分析表明：当夹片角度为7°时，锚环角度在6.5°～6.8°之间时锚具的承载能力可提高2.6%～4%。

参考文献：

[1]周 翔.高应力巷道高强锚索支护技术研究与应用[J].科技创业家,2012(21):99-99.

[2]康宏普,王金华,林 健.煤矿巷道锚杆支护应用实例分析[J].岩石力学与工程学学报,2010,29(4):649-664.

[3]李保军.夹片式锚具静载锚固试验中的影响因素[J].桥梁隧道,2012(9):234-235.

[4]赵 通,左德元,童建刚.夹片式锚固体系锥角的有限元参数化设计[J].西南交通大学学报,2004(5):614-617.

[5]曹志刚,李 俊.夹片式锚具锚固性能综合分[J].科技资讯,2011(19):96-96.

[6]陈宜强.夹片式锚具锚固失效原因及对策分析[J].城市建设理论研究,2011(32):234-236.

[7]邓 朗,妮 杨,帆康侃,等.夹片式碳纤维板锚具的有限元分析及设计[J].桂林理工大学学报,2012,32(1):72-76.

[8]简小刚,贾鸿盛,卞永明,等.夹片齿的啮合作用研究[J].中国工程机械学报，2011,9(2):151-156.

[9]于彩峰.钢绞线灌浆型锚夹具体系ANSYS有限元分析[J].科学实践,2010(13):262-263.

[10]谢翠红,秦 凯.矿用锚索力学分析及施工工艺[J].工业技术,2010(34):350-350.

[11]刘 彦.后张法锚具变形预应力损失的简化计算[J].沈阳建筑大学学报,2012,28(4):645-649.

[12]石亦平,周玉蓉.ABAQUS有限元实例详解[M].北京:机械工业出版社,2011:155-180.

[13]庄 茁,由小川,廖剑辉,等.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009:219-270.

[14]刘鸿文.材料力学[M].北京:高等教育出版社,2009:212-253.