光度非均匀彩色序列图像超分辨率重建
贾苏娟,韩广良,陈小林,孙海江
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春130033;2.中国科学院大学,北京100049)
1 引 言
随着彩色图像获取设备的普及和超分辨率重建技术的发展,彩色图像超分辨率重建成为研究的热点。现实中,外界光照变化或相机自动调节等因素导致观察到的序列图像光度不均匀,严重影响了图像质量及后续图像的使用。
目前图像超分辨率重建方法主要有两类,一类是基于重建的算法[1],一类是基于学习的算法,其中多种算法被应用在彩色图像超分辨率重建上。Elad[2]等将稀疏表示的方法用到彩色图像超分辨率重建上,图像通过训练的词典和稀疏矩阵的线性组合表示出来。Gevrekci和Gunturk[3]提出一种非线性模型进行光度匹配,进而对曝光量或照度不均匀的彩色图像序列进行重建。Capel[4]等首先提取图像的Harris角点进行运动估计,其次采用仿射变换模型进行光度匹配,最后采用概率估计法进行重建。Wen-Yi Zhao[5]等人分析了光照变化对重建结果产生的影响,提出一种两步重建法。首先生成物体的形状,最后再通过合成重加高分辨率的人脸图像。
考虑光度非均匀序列图像的超分辨率重建主要经过几何配准、光度配准、重建等步骤。在对光度不均的图像序列进行几何配准时,如果提取的特征对光照变化比较敏感,则容易造成误匹配,影响运动估计的精度。建立的光度模型要尽可能准确描述图像之间光度的变化。另外彩色图像比灰度图像蕴含更多的信息,因此在重建过程中还要考虑色彩的特征以及在重建过程中色彩通道之间的互相关性等。
基于上述分析,针对光度非均匀的彩色序列图像超分辨率重建,本文首先提取图像感兴趣区域的 方 向 梯 度 直 方 图(Histograms of Oriented Gradients,HOG)描述子,利用向量归一化相关系数作为相似性度量准则,选取相关系数最大位置作为匹配位置。通过构建光学测度模型估计测定参数,最后利用最大后验(Maximum a Posteriori,MAP)框架求出重建图像。不同于大多数超分辨率重建文章,本文考虑了图像获取过程中光度变化情况,处理对象是彩色图像。本文将HOG 描述子用在彩色图像运动估计方面,取得了较好的效果。
2 HOG 描述子提取
HOG 描述子的思想是:在一幅图像中,局部目标的表象和形状能够被梯度或边缘的方向密度分布很好地描述。HOG 特征在图像的局部细胞单元上操作,因此对图像的几何和光学形变都能保持很好的不变性。
HOG 描述子提取分为以下3步[6-7]:
2.1 计算梯度幅值和方向
梯度幅度m(x,y)反映灰度变化的大小,梯度方向θ(x,y)反映该像素点周围的灰度变化方向。用公式(1)、(2)计算梯度幅值和方向:
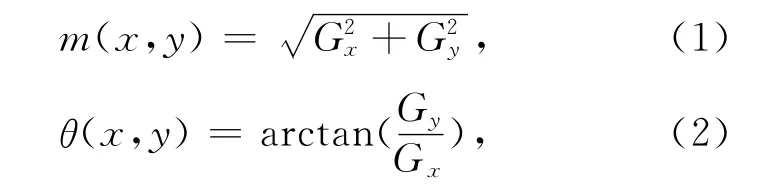
式中:Gx和Gy分别代表水平和竖直方向的梯度。θ(x,y)可以设置为0~π或0~2π。
2.2 构建并统计方向的直方图
求得图像的梯度后进行加权统计。将图像(IMAGE)划分成若干块(BLOCK),每个块又划分成若干细胞单元(CELL),如图1(a)所示。以CELL为单位统计梯度直方图,形成一个BIN 维的向量,如图1(b)所示。
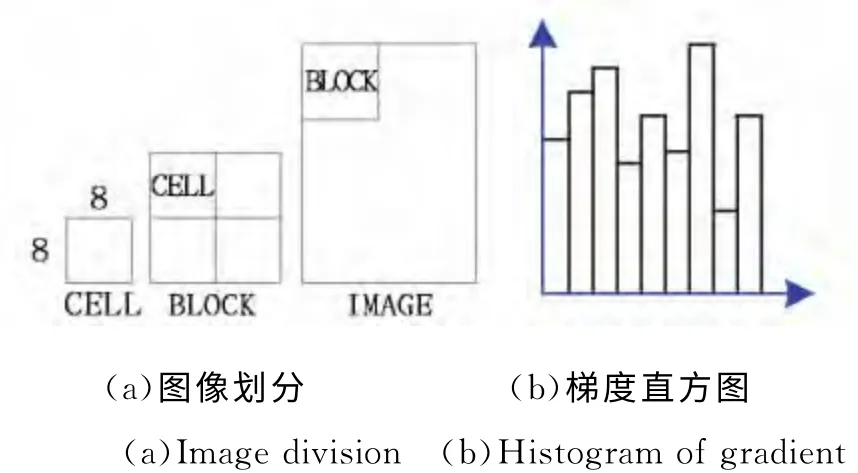
图1 图像划分和梯度方向统计直方图Fig.1 Image divided and histograms of oriented gradient
2.3 归一化和生成HOG 描述子
由于局部光照的变化以及前景-背景对比度的变化,使得梯度强度的变化范围非常大。以BLOCK 为单位对梯度强度做归一化。通过归一化,能对光照变化和阴影获得更好的效果。设V是BLOCK 对应的还未被归一化的向量,它包含BLOCK 的所有直方图信息,则标准化的向量nf可由公式(3)计算得到,式中ζ 为接近0的正数。最后将所有BLOCK 对应的向量按照空间顺序排列,形成HOG 特征描述子。

式中:L1-norm 是 曼 哈 顿 距 离,L2-norm 是 欧 几里德距离。
3 光度配准
在进行几何配准后,需要对图像间光度变化进行估计,以减小图像间的光度差异,此过程就是光度配准。本文假设处理的序列图像光度差异是全局的,且主要来源于相机自动调节或光照强度变化。本文采取一种仿射变换模型进行此项工作。
3.1 建立光度模型
对于每个RGB通道,两幅图像之间的变化可以通过一个光度模型来描述。该模型中共有两个参数:乘性因子α和加性因子β,这是需要估计的量。经过几何配准后,可以直接使用两幅图像对应像素的颜色计算这些参数。我们可以将一幅图像表示为三向量的矩阵变换:

3.2 模型简化和参数估计
多数情况下,公式(4)中的加性因子β可以忽略。由于光度变化是全局的,如果再把图像当成灰度图像处理,那么式(4)可以简化成如下模型:

假设两幅图像经过配准,那么可由两幅图像的均值比得到乘性因子α:

式中:IA、IB表示大小为的M×N 图像。
4 MAP算法原理
MAP[8-9]算法的基本思想是:超分辨率过程可以视为概率求解问题。假设低分辨率观测图像为Y,高分辨率图像为X,对图像退化过程进行如下建模:

式中:H 表示空间变换矩阵(包括运动变形、模糊和下采样过程),E 表示0 均值、自相关矩阵为N-1的加性Gaussian噪声。若视E 为白噪声,N是单位矩阵。如果X 也是均值为0、自相关矩阵为Q 的Gaussian随机过程,那么MAP估计变成MMSE估计子,

对式(8)进行最小化,则有

其中:
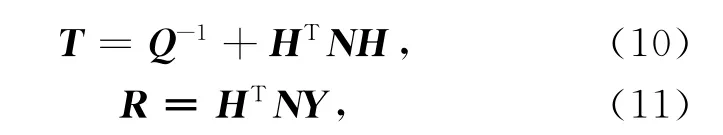
从上述求解过程可以看出,MAP 估计方法最终约化成可用迭代法[10]求解的巨型稀疏矩阵。
5 本文算法
本文假设对N 幅光度全局变化的低分辨率序列zk,k∈[I,N]进行重建。对图像成像过程建模:
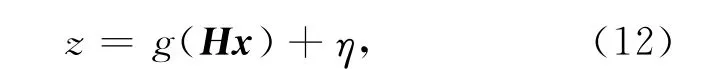
5.1 基于HOG 特征的运动估计
本文采用基于HOG 特征提取的方法进行运动估计。选取参考图像zr,输入图像zi,i=1,...,N,且i≠r,运动估计的实现步骤分为以下几步:
(1)对3个通道分别进行均方压缩,使用Sobel模板计算3个通道的梯度。
(2)梯度加权统计CELL 的梯度直方图,梯度模值决定投票的权重,梯度方向决定了投票至哪一个BIN。
(3)对每一个BLOCK(2×2CELL)进行归一化,对每一个区域输出一个梯度直方图向量作为该区域的HOG 特征。
(4)提取HOG 特征描述子后,利用向量归一化相关系数作为相似性度量准则。本文使用欧几里德距离描述两个向量的相关程度,选取相关系数最大位置作为匹配位置。
(5)计算zr、zi、间的空间变换矩阵Hi。
步骤(4)中,相关系数计算公式如下:
3)技术因素。主要考虑电能质量和用电量是否能满足ELV的充电需求,设备利用率是否能降低车辆充电时间成本。选取电能质量和用电量A31、充电站设备利用率A32作为技术因素的评价指标。

式中:X、Y 表示两向量,xi、yi表示向量坐标。
步骤(5)中,如果将匹配点对坐标转换至齐次坐标系下,Hi可由式(14)求出,其中(x1,x2,x3)、(x1′,x2′,x3′)是匹配点对对应坐标在齐次坐标下的变换:

5.2 算法流程
进行运动估计和光度配准后,在MAP 框架下使用迭代法求解高分辨率图像,同时为了避免大型矩阵求逆,本文使用梯度下降法求解x。
选定参考帧zr,首先对zr进行双线性插值,获取高分辨率图像初始估计值x(0)。设HTi(i=1,...,N)表示包含零插值、去模糊、去形变等过程的图像上采样过程矩阵。fri(·)(i=1,...,N)表示将输入图像zi经光度变换到参考图像zr的过程。自定义一个表示残差图像权值的对角线矩阵Wi,其对角线值为w(zi),那么MAP框架下使用迭代法求解高分辨率图像可由式(15)实现:

其中:γ为迭代步长。
算法框图由图2表示。
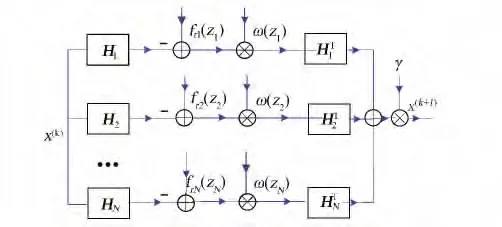
图2 算法框图Fig.2 Frame diagram of algorithm
6 实验结果与分析
6.1 图像评价函数
彩色图像的客观评价没有统一的标准并且很难与人眼的感官特性一致。为了评价实验数据,这里引入两类评价参数,一类是针对图像灰度信息的平均梯度与信息熵[11],另一类是图像对比度ICM[12]。
6.1.1平均梯度与信息熵
平均梯度反映了图像的微小细节反差和纹理变换特征,也反映了图像的清晰度。通常,平均梯度越大,图像就越清晰,反差也就越好。其计算公式如下:
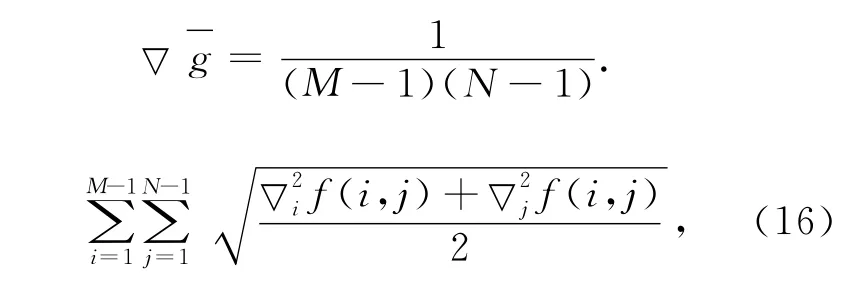
式中:f(i,j)、if(i,j)、jf(i,j)分别表示像点灰度及其在行、列方向上的梯度,M 和N 分别为图像的行、列数。
熵从信息论角度反映了图像信息丰富程度,其定义为:

式中:L 表示图像的最大灰度级,Pi为图像X 上像元灰度值为的概率。当各个灰度级出现的概率均为Pi=1/L,即像素在各个灰度级均匀分布时,熵H(X)具有最大值,为lg(L)。此时图像的灰度分布最均匀,层次最多,信息量最丰富;当图像的所有像素只有单一灰度级时,熵具有最小值0,此时无图像信息。
6.1.2 图像对比度
图像对比度(ICM)基于灰度及彩色直方图信息,采用L*a*b*颜色空间。其中L*为米制明度,a*、b*为米制色度。ICM 定义如式(18)所示:
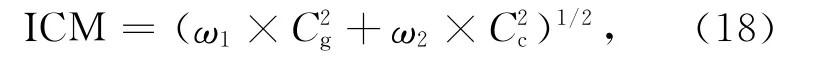
其中:Cg是灰 度 对 比 度,Cc是 彩 色 对 比 度,ω1和ω2是Cg与Cc的 权 重,Cg与Cc的 计 算 公 式 如(19)所示,ICM 的值为[0,1],0表示图像对比度最差,1表示图像对比度最好。
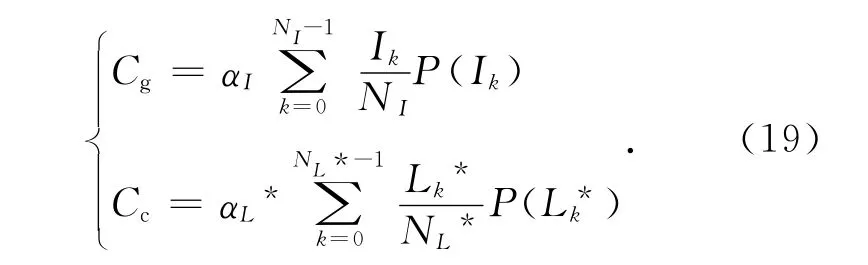
6.2 实验结果与分析
实验平台为MATLAB7.0(2010b),CPU 为Intel(R)Core(TM)i3-2120,主频是3.30GHz,显卡为Intel(R)HD Graphics Family。为比较本文算法在超分辨率重建上的有效性和对光度变化的鲁棒性,进行了两组实验。由于版面原因,对图像进行缩小处理。
6.2.1 重建实验和评价
本组实验对实拍彩色序列进行超分辨率重建。对作者所在实验室的窗台进行连续拍摄,获得18幅320×240低分辨率序列图像。图3中是实验序列中的第3、9、15帧。

图3 三帧低分辨率图像Fig.3 Three frames of low resolution images
为了评价重建图像的质量,以单帧插值方法与本文重建算法进行对比实验。本次实验未进行光度配准,放大因子为2,迭代次数为4,插值方法为双线性插值法。第9帧插值与重建效果如图4(a)、(b)所示,截取图像中200×200的区域进行插值和重建细节比较,如图4(c)所示。


图4 第9帧插值图像和重建图像Fig.4 Single frame interpolation images and reconstruction images
采用平均梯度和信息熵对重建图像进行评价,计算结果如表1、表2所示。

表1 插值和重建图像的平均梯度Tab.1 Average gradient of the interpolated images and reconstruction images

表2 插值和重建图像的信息熵Tab.2 Information entropy of interpolated images and reconstruction mages
目测评价序列中重建图像与单帧插值图像质量,可以看出重建图像明显比插值图像清晰。由表1和表2看出,重建图像的平均梯度与信息熵均比单帧图像大,表明重建图像更清晰、所含信息量更丰富。实验表明,基于HOG 特征进行运动估计的MAP算法能够取得满意的重建效果。
6.2.2 光度鲁棒性实验和评价
本组实验首先验证算法的普适性。选取经典Lena图像,大小为256×256。对其进行高斯模糊、亚像素平移并进行2 倍下采样,生成4 幅128×128的低分辨率序列图像。对每一低分辨率图像进行全局曝光量调节,在低分辨率图像上分别增减相等数量的曝光量。经处理获得12幅曝光量不同的彩色序列图像。实验共进行两次,一次只进行几何配准和重建,另一次进行几何配准、光度配准和重建。图5是128×128低分辨率序列图像中的三幅。

图5 3帧曝光量不同的图像Fig.5 Three frames of different light exposure
设置放大因子为2,迭代次数为4,重建后的图像尺寸为256×256。两次实验重建图像与插值图像列于表3中。

表3 实验结果对比Tab.3 Comparison of the experiment results
计算图像的平均梯度、信息熵和ICM,结果如表4~6所示,表6中LR 图像表示原始低分辨率图像。
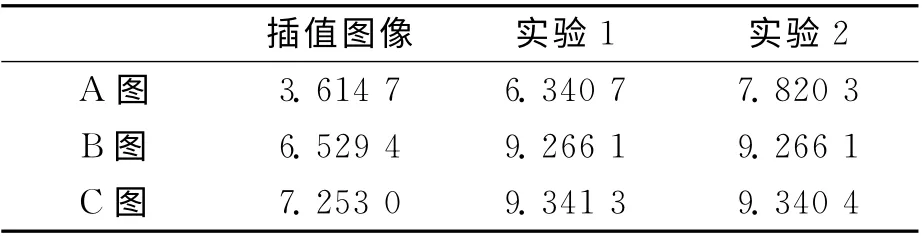
表4 平均梯度对比Tab.4 Comparison of average gradient
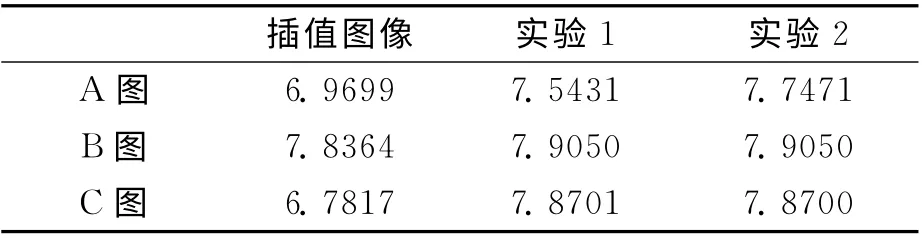
表5 信息熵对比Tab.5 Comparison of Information entropy
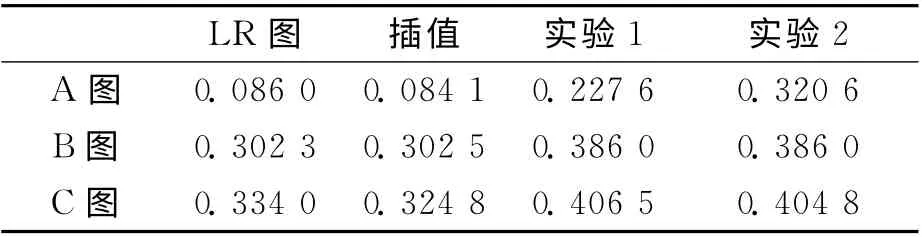
表6 图像对比度Tab.6 ICM of relative images
结果表明,本文算法明显优于插值算法,能够显著提高图像的清晰度和信息丰富程度。对于曝光量不足的A 图,光度配准能够提高图像的平均梯度和信息熵。但是对于曝光正常的B 图和曝光过度的C 图,经光度配准的算法与未经光度配准的算法得出的结果几乎一样,也就是不能提高图像的平均梯度和信息熵,即不能使图像更清晰或信息更丰富。
由图像对比度(ICM)计算结果看出,插值算法也不能改善图像的对比度,对于曝光不足或曝光过度的图像,甚至会减小图像的对比度,降低图像质量。实验1 结果表明,采用的几何配准与MAP 重建算法已能够大幅提高图像对比度,对曝光不足或曝光过度的图像,其ICM 提高了0.1左右。实验2是本文的完整算法,所得结果最优。A 图是曝光不足的图像,经光度配准后的图像对比度比未经光度配准的提高了40%左右,主观看起来图像“变亮了”;C图是曝光过度的图像,经光度配准后对比度几乎不变,但是主观看起来图像“变暗了”,视觉效果更好。
为进一步验证本文算法对光度非均匀变化的鲁棒性及算法的实用性,本文对相机的积分时间进行调节,仍对实验1中的窗台进行拍摄,获取一系列光度非均匀变化的图像。选取其中9幅分别使用双线性插值算法及本文提出的算法进行重建。图6为9幅图像中的3幅,大小均为320×240。
设置放大系数为2,进行4次迭代,插值算法及本文算法的重建结果如表7所示。计算图像的平均梯度、信息熵及图像对比度ICM,计算结果如表8~10所示。

表7 重建效果对比Tab.7 Comparison of reconstruction
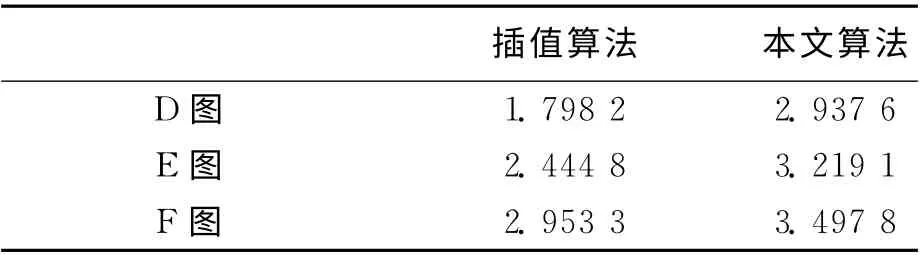
表8 平均梯度对比Tab.8 Comparison of average gradient

图6 3幅曝光量不同的图像Fig.6 Three frames of different light exposure

表9 信息熵对比Tab.9 Comparison of information entropy
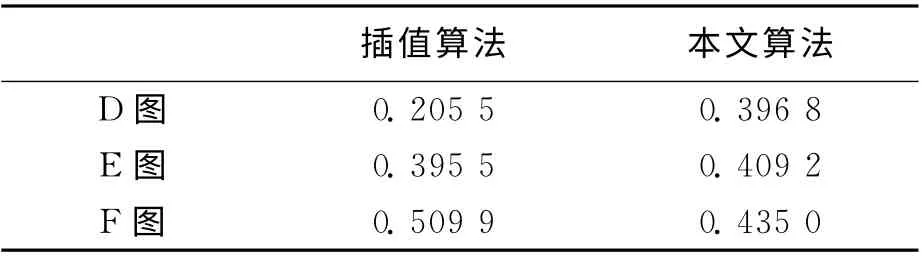
表10 图像对比度Tab.10 ICM of relative images
通过计算重建图像的平均梯度、信息熵及图像对比度可知,本文算法对实拍光度非均匀序列图像的重建依然有效。使用文本算法重建的图像无论是平均梯度还是信息熵都明显高于双线性插值算法重建出的图像。由表7及表10的图像与数据可知,经过光度配准后的重建图像改善了图像对比度。D 图对比度比插值算法的高出近一倍左右,使得原来暗的图像变亮了。F 图的对比度则下降了0.0749,视觉上变暗了。综上所述,本文算法能够提高重建图像的清晰度和信息丰富程度,并对光度变化具有一定的鲁棒性。
7 结 论
提出一种光度非均匀彩色低分辨率序列图像超分辨率重建算法。算法采用基于HOG 特征的方法进行运动估计,通过建立光度模型进行光度配准,采用MAP算法进行重建。实验表明,该算法对外界光照变化或相机自动调节等情况造成的图像光度变化具有一定的鲁棒性,在该种情况下也能实现较高质量的超分辨率重建。本文工作为彩色视频序列超分辨率重建或高动态场景生成奠定了基础,具有一定的理论及工程意义。
[1] Park S C,Park M K,Kang M G.Super-resolution image reconstruction:a technical overview[J].IEEE Signal Processing Magazine,2003,20(3):21-36.
[2] Mairal J,Elad M,Sapiro G.Sparse representation for color image restoration[J].IEEE Transactions on Image Processing,2008,17(1):53-69.
[3] Gunturk B K,Gevrekci M.High-resolution image reconstruction from multiple differently exposed images[J].IEEE Signal Process Letters,2006,13(4):197-200.
[4] Capel D,Zisserman A.Computer vision applied to super resolution[J].IEEE Signal Processing Magazine,2003,20(3):75-86.
[5] WenYi Zhao,Sarnoff C.Super-resolution with significant illumination change[C]//Proc.Int.Conf.Pattern Recognition,Singapore:Image Processing,2004:1771-1774.
[6] 曹治国,吴博.采用HOG 特征下的视景象匹配算法[J].红外与激光工程,2012,41(2):514-516.Cao Z G,Wu B.Approach on scene matching based on histograms of oriented gradients[J].Infrared and laser engineering,2012,41(2):514-516.(in Chinese)
[7] Dalal N,Triggs B.Histogram of oriented gradients for human detection [C]//International Conference on Computer Vision and Pattern Recognition,San Diego,USA:Computer Vison and Pattern,2005,2:886-893.
[8] Schultz R R,Meng L.Subpixel motion estimation for super-resolution image sequence enhancement[J].Journal of Visual Communication and Image Representation,1998,9(1):38-50.
[9] 江静,张雪松.图像超分辨率重建算法综述[J].红外技术,2012,34(1):24-30.Jiang J,Zhang X S.A review of super-resolution reconstruction algorithms[J].Infrared Technology,2012,34(1):24-30.(in Chinese)
[10] 张剑.图像超分辨率重建问题研究[D].长沙:中南大学,2010.Zhang J.Research on super resolution reconstruction of images[D].Changsha:Central South University,2010.(in Chinese)
[11] 邓建青,刘晶红,刘铁军.基于DSP系统的超分辨率图像重建技术研究[J].液晶与显示,2012,27(1):114-119.Deng J Q,Liu J H,Liu T J.Super-resolution image reconstruction technology based on DSP system[J].Chinese Journal of Liquid Crystals and Displays,2012,27(1):114-119.(in Chinese)
[12] Yuan Y H,Zhang J J,Chang B K,et al.Objective quality evaluation of visible and infrared color fusion image[J].Optical Engineering,2011,50(3):033202(1-11).

