双三次卷积模板插值算法的FPGA实现

陈志杰，凌朝东，魏腾雄

（华侨大学 信息科学与工程学院，福建 厦门361008）

1 引 言

在很多的场合需要高分辨率的大图像显示，现在受限于液晶和信号传输，单个液晶屏并不能做的非常大，所以现在一般采用多个液晶屏进行拼接来实现大分辨率大图像的显示，为了使不同的原始输入图像的分辨率能够在拼接大屏幕上匹配显示，就必须对输入的视频图像进行缩放以匹配输出的分辨率，满足拼接屏幕的要求［1］。这是插值算法在缩放上的一个应用实例，插值算法的应用很广泛，除视频图像缩放，视频图像的旋转也会用到插值算法。

现代的插值算法包括线性和非线性插值、有理插值、曲面重构和自适应区域插值等，但很多算法都由于过于复杂难于在硬件上实现，在硬件上实现常用的插值算法有最邻近插值算法，双线性插值算法，双三次插值算法等［2］。最邻近插值简单且直观，但得到的图像质量不高。双线性内插值法计算量大，具有低通滤波器的性质，使高频分量受损，所以可能会使图像轮廓在一定程度上变得模糊［3］。双三次插值法用16个相邻点做插值，它消除了最邻近插值的阶梯状边界问题，解决了双线性插值模糊的问题能够克服以上两种算法的不足，计算精度高，但计算量大［4－7］。本设计采用双三次插值算法，但为提高计算效率，对双三次插值计算进行了离散化处理，变实数运算为整数运算［8］。有效克服双三次插值算法计算量大的问题。提出了实现双三次卷积模板算法的硬件电路的实现方法，避免三次方的计算，使次算法能够在没有显著增加硬件资源的同时得到令人满意的图像缩放效果。

2 双三次插值算法

2.1 基函数数学模型

在数值分析中，插值算法可用通式表示为

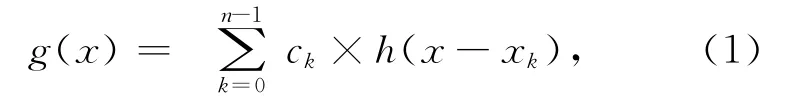
其中：h（x－xk）为插值基函数，ck为第k 个原函数的值。不同的插值算法只是基函数及选取的插值点个数n不同。如果基函数的最高次幂为三次且在定义域内基函数的一阶、二阶导数连续，则称该算法为三次插值算法，若在二维方向上应用该算法即双三次插值算法。

系统采用Keys提出的三次插值基函数，双三次插值算法基函数是利用三次多项式h（ω）来逼近理论上最佳插值函数sin（π×ω）／（π×ω），其基函数h（ω）的表达式如下：

2.2 实现过程

图像为二维信号，所以，图像缩放的插值算法要在二维方向应用上述算法。先在水平方向，假设所求插值像素点为F，首先，每一行依据上述插值原理，得到4 个临时插值像素点的像素值F0，F1，F2，F3。

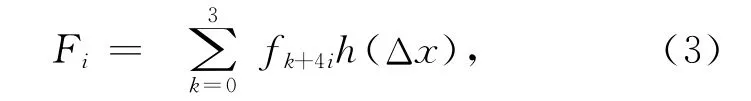
其中：Fk＋4i为输入图像邻近16个点的像素值，两像素点的距离为单位1。然后，以Fi为原函数，在垂直方向依据同样的原理求得所需插值点F 的值，即

2.3 算法离散化，模板化实现方法

由上述可知计算时需要h（Δx）和h（Δy）这两个值，如果Δx 和Δy 直接代入基函数进行计算，需要大量的乘法和浮点运算，会占用大量的系统资源，这里采用将h 的值离散化，模板化进行计算。计算每一目标像素灰度值，需要计算出目标像素点和源像素点的水平、垂直距离，然后根据距离带入公式算出相应的加权系数。

将水平距离和垂直距离Δx，Δy 平均分割为4份，Δx，Δy 都在［0，1］的范围内，分为［0，1／4］，［1／4，1／2］，［1／2，3／4］，［3／4，1］，如果Δx，Δy 的值落入到这4个范围中的一个，将Δx，Δy 都取这个范围内的平均值，即如果在［0，1／4］则取1／8，如果在［1／4，1／2］则取3／8，如果在［1／2，3／4］则取5／8，如果在［3／4，1］则取7／8。

在进行水平方向的卷积时需要用到

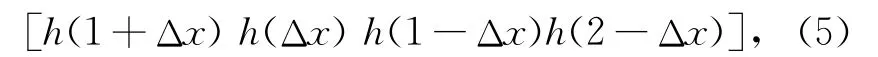
这个为加权系数，计算一个点的时候需要4个像素的点和这个加权系数进行卷积。按上面的范围进行计算加权系数，得到水平方向加权系数的4个目标（每个数左移18位，用移位计算在硬件里方便实现）：

同理垂直方向

3 插值算法的FPGA 实现

3.1 实现框图

FPGA 采用的是Lattice的ECP3 系列的芯片，其框图如图1所示。

图1 FPGA 实现的原理图Fig.1 Block diagram of FPGA implementation

如图1所示，数据进入到FPGA 后进行水平方向的插值计算，水平方向计算完，由于计算垂直插值时需要用到图像相邻的4行数据，所以将水平方向插值计算结果的数据送入外部的存储器进行存储，然后从外部存储器中读出数据进行垂直方向的插值。

3.2 行卷积的实现

根据上面的分析，行卷积的实现为取相邻的4个像素点与相应的模板进行卷积计算得到结果。所以行卷积的计算就是如何取得相邻的4个像素点和如何取得相应的模板。在一行上4个相邻的像素点需要同时取得，这样才能提高计算速度，为了同时得到4个相邻的像素点，输入缓存用4个双口RAM，在视频图像进入FPGA 时，将一行的数据同时写入4个RAM 中，同时读取时4个RAM取相邻地址的数据，就得到了一行中4个相邻的像素点。而相应的模板需要根据缩放的比例来进行计算得到。图2为行卷积实现的框图。

需要根据缩放比例计算出目标像素点对应到源像素点的位置，这个用scale factor 模块来实现，知道目标像素点对应到源像素点的位置就能得出需要的模板。缩放比例用一个16.16的定点小数来实现，高16位表示整数部分，低16位表示小数部分。计算时采用累加来实现，每一次都加上缩放比例，这样就能得到相邻的4个像素点和相应的模板。其modelsim 的仿真结果如图3所示，仿真时采用放大1.6 倍时一行图像数据的情况。

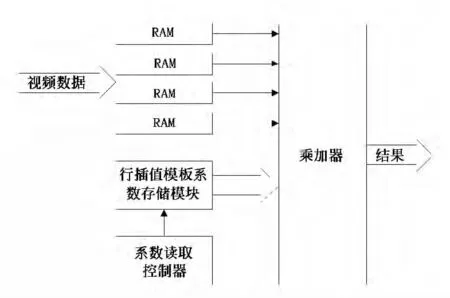
图2 行卷积实现原理图Fig.2 Block diagram of line convolution implementation

图3 scale＿factor的仿真波形Fig.3 Waveform of scale＿factor simulation

其中line为目标图像对应到源图像的整数部分的值，x＿distance为对应到源图像的小数的值，这样根据整数部分可以得到相邻的4个像素点，根据距离可以得到相应的模板。其中x＿distance小数部分为左移16 位的结果。根据上面的计算可以得到卷积的像素点和模板，然后将得到的数据送入乘加器就能得到行卷积的计算结果。乘加器用Lattice芯片上的硬件乘加器进行实现，硬件乘加器的速度能够满足要求。

对行卷积整体仿真时，利用matlab采集一整幅图片的像素点，将图片的像素点转化成RGB的格式，用十六进制存在文本中，然后利用modelsim 对文本的读写功能，产生一个模拟的VGA时序视频信号，信号包括时钟信号、行同步信号、场同步信号、数据使能信号和数据信号。将这几个信号在testbeach中生成，给行卷积的模块，将行卷积的计算结果通过modelsim 对文本的操作写入到文本当中，将得到的仿真文本的数据和matlab仿真数据进行比对，做到两个仿真结果的数据是一样的，说明硬件描述语言对算法的行卷积能够实现。

3.3 外部存储器

系统支持1 080p高清视频，1 080p视频的分辨率为1 920×1 080，如果当视频的帧率为60 Hz时，RGB每位采用8bit，这样一帧图像的大小为1 920×1 080×24bit约为2M×24bit，进行处理时为了提高计算效率采用乒乓操作，所以一帧需要的存储为4M×24bit，所以采用一片512M 的，数据宽度为16bit的DDR3 就能满足图像缓存的需要。DDR3的写入速度非常快，比视频的像素流快，所以，我们不可能来一个像素写入一个值，这样操作繁琐，这就有必要在前面做一个像素的缓存器，如果视频图像的一行像素数据存入到缓存中时，将缓存中的数据一起写入到DDR3。

DDR3控制器利用现有的IP 核来实现。其实现框图如图4所示。

图4 DDR3控制器实现框图Fig.4 Block diagram of DDR3controller

主要包括4个FIFO，4个FIFO 分别为发生请求读写DDR 时，将请求读写ddr的地址放入fifo中。ddr＿init模块主要是负责ddr的初始化，ddr＿ctrl＿state主要负责处理DDR 进行读写的状态控 制，ddr3＿sdram＿mem＿top 是Latticed 的DDR3的IP核。

其中ddr＿ctrl＿state的内部是设计一个状态机，来实现ddr的读写控制状态，其状态转移图如图5所示。

以下是各个状态所表示的含义：

上电相关状态：

S＿POWER＿UP表示上电开始状态。

图5 DDR 的状态转移图Fig.5 State diagram of DDR ctroller

S＿CHIP＿CONFIG 表示芯片配置状态。

S＿CONIG＿END 表示等待芯片配置完成状态。

S＿IDLE表示系统空闲等待状态。

读DDR 相关状态：

S＿RD＿RQ0表示读DDR，读取FIFO 得到位置数据。

S＿RD＿RQ1表示读DDR，读取FIFO 得到位置数据。

S＿RD＿RQ2表示读DDR，读取FIFO 得到位置数据。

S＿RD＿RQ3表示读DDR，读取FIFO 得到位置数据。

S＿WAIT＿RD＿RQ 表示需要几个时钟（m2～m4），从FIFO 中读出位置参数。

S＿DDR＿RD＿CMD 表示位置参数准备好，对DDR IP写入读命令和相应地址。

S＿WAIT＿RD＿END 表示等待DDR 将数据读完。

写DDR 相关状态：

S＿WR＿RQ0表示写1端口数据状态。

S＿WR＿RQ1表示写2端口数据状态。

S＿WR＿RQ2表示写3端口数据状态。

S＿WAIT＿WR＿RQ 表示需要几个时钟（m2～m4），从FIFO 中读出位置参数。

S＿DDR＿WR＿CMD 表示位置参数准备好，对DDR IP写入读命令和相应地。

S＿WAIR＿WR＿END 表示等待DDR 将数据写完。

3.4 列卷积的实现

列卷积的计算方法和行卷积的计算方法相同，其实现框图如图6所示。只是列卷积时需要得到相邻四列的像素值，这个可以通过每次从DDR3中读出相邻的四列放入4 个RAM 中，这样从每一个RAM 中可以得到相邻四列的4个像素值。

其中DDR 数据读取控制模块主要是根据图像插值算法的需要从DDR 中读出相邻的4 行，分别放入到4 个RAM 中，然后通过控制RAM的地址来读取列相邻的4 个像素点。同时系数读取控制器也根据需要读出相应的列插。

图6 列卷积实现框图Fig.6 Block diagram of column convolution implementation

3.5 资源使用情况

此算法是在Lattice ECP3－17EA 来实现的，图7为实现此算法的资源的情况，从图片中可以看出这个算法占用的资源不是很多，所以在此FPGA 芯片上实现此算法还是可行的。

3.6 结果与讨论

做试验时，先用matlab 将算法用软件来实现，将仿真得到的结果保存。通过硬件描述语言实现后，用modelsim 仿真，同样利用modelsim的读写功能，对一张图片进行仿真，结果保存在文件里，将matlab得到的结果和modelsim 得到的仿真结果进行比较，可以发现两个结果是完全一样的。说明用硬件语言实现了该算法。

图7 FPGA 资源的使用情况Fig.7 Use of FPGA resources

将双三次插值算法改成模板方法实现，省去了很多的浮点计算，使其在硬件上耗费更少的资源。将图像看成二维的，先计算水平的插值，再算垂直的插值，这样在硬件上也可以减少资源，水平和垂直同时计算，一次要取临近的16个点，然后进行16个乘加运算，而先水平后垂直，一次只需取4个点，需要4个乘加运算，相当于需要两次的4个乘加运算。这样可以减少乘加器的数量。

4 结 论

双三次插值算法能够得到令人满意的图像缩放效果，但因其算法复杂，硬件上实现很少应用，而本文通过分析双三次插值的基本原理，提出了将图像分为二维来进行计算，先水平后垂直实现双三次插值算法的硬件实现思路。同时将计算过程离散化，化浮点计算为整数计算，避免了三次方的计算。通过实验可以发现，利用FPGA 实现双三次卷积模板算法可以比实现双三次插值算法节约硬件资源。同时可以得到不错的图像效果，适合工程的应用。

［1］ Xiang Z Q，Zou X C，Liu Z L.An high quality image scaling engine for large－scale LCD［C］.ICSP2006 Proceedings，Wuhan，China：ICSP，2006.

［2］ 王增发，孙丽娜.CFA 图像实时插值在FPGA 上的应用［J］.液晶与显示，2013，28（4）：615－619.Wang Z F，Sun L N.Application of CFA images interpolation algorithm in FPGA real－time system ［J］.Chinese Journal of Liquid Crystals and Displays，2013，28（4）：615－619.（in Chinese）

［3］ 孙红进.FPGA 实现的视频图像缩放显示［J］.液晶与显示，2010，25（1）：130－133.Sun H J.FPGA realization of video lmage zooming display［J］.Chinese Journal of Liquid Crystals and Displays，2010，25（1）：130－133.（in Chinese）

［4］ 张阿珍，刘政林，邹雪城，等.基于双三次插值算法的图像缩放引擎的设计［J］.微电子学与计算机，2007，24（1）：49－51.ZHANG A Z，LIU Z L，ZOU X C，et al Design of image scaling engine based bicubic interpolation algorithm［J］.Microelectronics ＆Computer，2007，24（1）：49－51.（in Chinese）

［5］ 王会鹏，周利莉，张杰.一种基于区域的双三次图像插值算法［J］.计算机工程，2010，36（19）：216－218.Wang H P，Zhou L L，Zhang J.Region－based bicubic image interpolation algorithm ［J］.Computer Engineering，2010，36（19）：216－218.（in Chinese）

［6］ Li Y H，Zhen J，Li J H，et al.The hardware realization of the bicubic interpolation enlargement algorithm based on FPGA［C］／／Third International Symposium on Information Processing，Qingdao，China：ISIP，2010：277－281.

［7］ Nuno－Maganda M A，Arias－Estrad M O.Real－time FPGA－based architecture for bicubic interpolation：An application for digital image scaling［C］／／Proceedings of the 2005 International Conference on Reconfigurable Computing and FPGAs，Puebla City，Mexico：Computer Society，2005：31－42.

［8］ 高成敏，陈良，林永和.双三次卷积模板算法［J］.计算机工程与应用，2009，45（17）：151－154.Gao C M，Chen L，Lin Y H.Bicubic convolution template algorithm［J］.Computer Engineering and Applications，2009，45（17）：151－154.（in Chinese）

［9］ 樊博，王延杰，孙宏.FPGA 实现高速实时多端口图像处理系统的研究［J］.液晶与显示，2013，28（4）：620－625.Fan B，Wang Y J，Sun H.High speed real－time multiport image algorithm in FPGA real－time system［J］.Chinese Journal of Liquid Crystals and Displays，2013，28（4）：620－625.（in Chinese）