基于第一性原理的力磁耦合模型研究

刘　斌，张　威，杨茗涵，张　强

(沈阳工业大学信息科学与工程学院，辽宁沈阳　110870)

0　引言

残余应力是材料生产和加工过程中不可避免的，属于材料的内部应力(固有应力)，在材料的使用过程当中，这些残余应力与外部的疲劳载荷叠加在一起，从而影响材料的磁性能和机械性能。金属磁记忆(MMM)作为一种新兴的无损检测方法可以有效的检测金属构件的应力集中区域。该方法在管道、锅炉、钢轨等领域已有较成功的应用[1-4]。

文中运用量子力学相关理论分析了铁磁材料磁性的来源，并采用密度泛函理论的第一性原理平面波赝势法，计算了晶体磁性能随载荷作用的定量变化关系，分析了金属构件应力集中区域表面漏磁信号的变化特征，为金属检测技术的深入研究提供了一种新的方法。

1　磁记忆效应的微观原理

根据量子理论，原子中满壳层电子的总磁矩为零，对原子的固有磁矩没有贡献，只有未满壳层中的电子才能产生净磁矩。

电子运动的轨道磁矩和自旋磁矩为：

(1)

(2)

(3)

式中：l为轨道角度动量；s为自旋角度动量。

gs通过实验测定，通常取gs=2，不至于有明显误差。若原子未满壳层中只有1个电子，则原子磁矩为：

(4)

式中：j为原子的总角动量，j=l+s.

(5)

式中：g为兰德因子。

由式(5)两端点乘J之后得到，即：

(6)

原子角动量的关系有：

(7)

(8)

在微观世界里，角动量都是量子化的，所以有：

L2=L(L+1)h2

(9)

S2=S(S+1)h2

(10)

J2=J(J+1)h2

(11)

(12)

所以原子净磁矩为

(13)

式中：μB为玻尔磁子，是原子磁矩的天然单位。

原子内的原子磁矩来源于未满壳层的电子自旋，电子轨道运动处于基态，对磁性没有贡献。Fe属于3 d过渡金属，每个原子由3 d壳层引起的固有磁矩在相邻原子间量子力学的相互作用下趋于平行排列，从而体现很好的铁磁性。在自旋极化体系中，多数自旋电子和少数电子占据着不同的能量状态，分别计算它们的态密度分布，两者之和为总态密度，两者之差为自旋态密度(SDOS)，自旋态密度是影响材料磁性能的关键因素。

铁磁材料在无外场作用时净磁矩可以表示为所有原子磁矩之和：

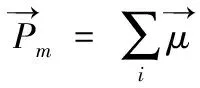
(14)

固体的磁化强度M定义为单位体积中的磁矩，即：

(15)

在地磁环境下，总的磁感应强度为：

B=B0+B1

(16)

地磁场产生的磁感应强度B0=μ0H，固体自身的磁感应强度B1=μ0M，所以有：

(17)

2　计算方法及步骤

铁磁材料体心立方晶体结构的磁特性受外力的影响较大，面心立方和六角结构的磁特性几乎不受外力影响。金属磁记忆应力检测技术主要应用于钢铁构件的应力检测。文中以低碳钢为例，以bcc结构Fe(α-Fe)为初始研究对象，采用Castep程序包建立了α-Fe的力-磁耦合模型，研究磁记忆效应机理。如图1所示，在α-Fe单原胞体心立方结构中，体心处的原子为一个原胞所有，顶角处原子为8个原胞共有，所以单原胞中共有2个电子。

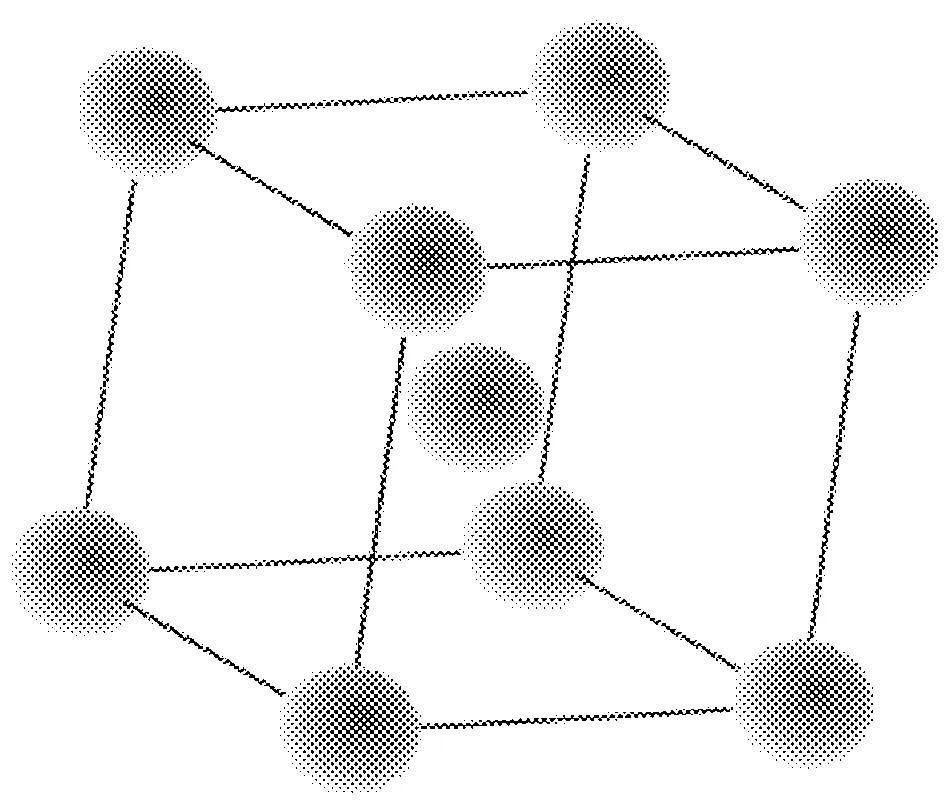
图1　α-Fe晶体结构

以α-Fe为初始研究对象，计算磁性参量时考虑自旋极化。采用基于密度泛函理论的赝势平面波法时，平面波基函数的截止能取400 eV，布里渊区积分采用Monkhorst_pack方法，用16×16×16的点抽样对应简约布里渊区含576个点；这种选择使得由布里渊区数值积分及平面波基函数的截断能这两项数值计算误差满足所设定的能量误差要求(0．01 eV/atom)；采用广义梯度近似(GGA)法处理交换关联势能，由此计算磁记忆效应的力-磁耦合关系。

3　计算结果与讨论

根据量子力学理论，力-磁耦合体系必须满足能量最小化原则，这样系统才能处于稳定状态，在稳定状态下，电子态密度分布情况才能正确反映力对原子磁矩的影响。如图2所示，体系优化计算过程是收敛的，说明在文中对交换关联能采用的近似算法和对电子波函数采用的平面波赝势展开法是合理的，求解出的是体系正确的密度分布，是最低的能量。

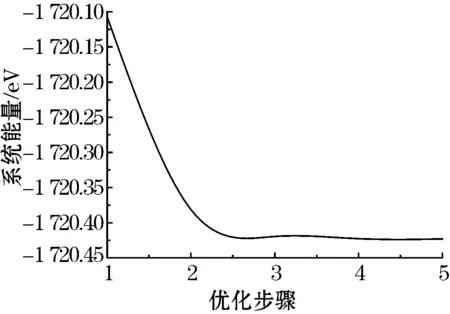
图2　模型优化

在磁记忆检测模型计算中，模型的优化结果收敛只能说明该模型满足单电子方程的自洽运算。证明模型建立的正确性，需要与量子力学相关实验数据比较。在设定能量计算精度为0．01 eV/atom后，首先计算了模型平衡态性质，如表1所示。文中采用GGA法计算的晶格常数、原胞体积和原子磁矩与量子力学实验值符合很好。这是由于GGA法显著修正在低电荷密度区域的指数公式形式，引入了与电荷梯度的相关性。所以用GGA法来计算磁记忆效应的磁力学关系。

表1　第一性原理计算结果的比较

Fe属于3 d过渡金属，每个原子由3 d壳层引起的固有磁矩在相邻原子间量子力学的相互作用下趋于平行排列，从而体现很好的铁磁性。模型基态能带结构如图3所示，在费米面附近不存在禁带区间，为典型的金属型物质。由于多数自旋电子和少数自旋电子占据着不同的能量状态，具有不同的空间波函数，造成它们所处能带的能级发生相对位移，一个能带的费米能级上升，形成主能带；另一个能带的费米能级下降，形成副能带，其形状对过渡金属的磁性能有着重要影响。

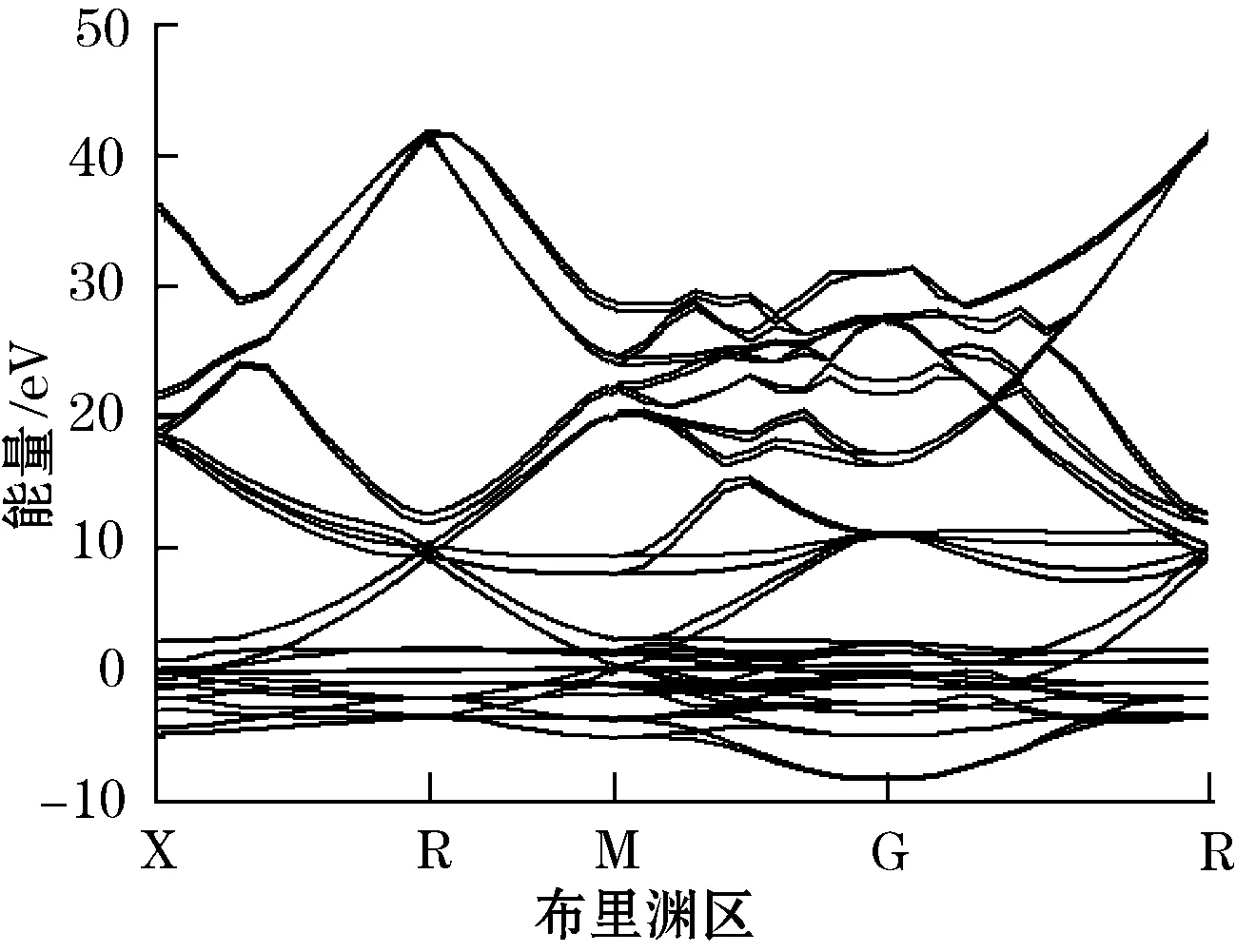
图3　能带结构

在自旋极化体系中，体系磁矩随压强的变化与微观结构的改变密切相关，自旋态密度是影响材料磁性的关键因素。图4为两种自旋电子总的态密度分布，费米能级附近主副能带具有很大的劈裂，说明Fe显示出很好的铁磁性。图5为d轨道电子的分波态密度分布，可以看出d轨道电子在费米面附近的分波态密度分布与体系的自旋态密度分布相似，费米能级附近主副能带劈裂较大且峰值很大，说明d-电子对体系磁特性有着重要的贡献。图4、图5中，态密度的单位为每电子伏特的能量状态含有的电子数。

图4　自旋态密度分布图

图5　轨道电子分波态密度分布图

为研究金属磁记忆效应的力-磁耦合关系，计算分析了压强对体系结构参数和磁特性的影响。从图6曲线可以看出，原子体积随外界压强的增加近似线性减小。压强增加导致了晶体结构趋于密堆积，这种趋势在物理上是合理的。

α-Fe自旋极化计算得到的原子磁矩与压强的关系如图7所示，随压强的升高原子磁矩线性减小，说明外力会影响材料磁性特性的变化，外力作用导致晶格畸变是磁记忆效应产生的主要原因。

4　结束语

金属磁记忆检测技术已被广泛应用于铁磁构件应力集中区域的早期诊断。与传统的漏磁检测技术相比，具有诊断速度快、操作简单、价格低廉等优势。但是，目前没有理论模型来描述磁记忆技术中应力集中与自发漏磁信号的关系。文中采用密度泛函理论平面波赝势方法，在广义梯度近似下计算了压力对晶格结构和原子磁矩的影响。其中一个重要的结果是：随压力升高原子磁矩线性减小，晶格畸变是磁记忆自发漏磁信号产生的主要原因。文中的研究工作从理论上解释了磁记忆自发漏磁信号产生的原因，为进一步研究金属磁记忆效应的物理机理提出了新方法。

图6　原子体积与压强关系

图7　原子磁矩与压强关系

参考文献：

[1]DOUBOV A A．Express method of quality control of a spot resistancewelding with usage of metal magnetic memory．Welding in theWorld，2002，46(S)：317-320．

[2]DOUBOV A A，DEMIN E A，MILYAEV A I，et al．The experience of gas pipeline stress-strain state control with usage of the metal magnetic memory method as compared with conventional methods and stress control means．Welding in the World，2002，46(9/10)：29-33．

[3]唐继红，潘强华，任吉林．静载拉伸下磁记忆信号变化特征分析．仪器仪表学报，2011，32(2)：336-341．

[4]WANG Z D，YAO K ，DENG B，et al．Theoretical studies of metal magnetic memory technique on magnetic flux leakage signals．NDT&E International，2010，43(10)：354-359．