基于相关峰值插值法的超声应力测量

巢　旭，华云松，吴　莹

(上海理工大学光电信息与计算机工程学院，上海　200093)

0　引言

构件的内部应力，特别是其残余应力是一项重要的力学参数，决定了构件的力学性能，如静力强度、疲劳强度、几何变形及抗腐蚀能力等。为了消除构件的残余应力，确保其安全性和可靠性，工程技术人员必须利用检测技术测定构件残余应力分布的情况。对于应力的测量，在国内外已开展多年，已形成多种测量方法[1]。在这些测量方法中，超声波法具有便于现场测量、既能测表面又能测内部应力以及对构件无损等特点，因此，利用超声波法对应力进行测量的潜力是不言而喻的。由于受到采样精度、采样率、电路噪声和测试现场环境噪声的影响，采集的超声信号中不可避免地存在误差和噪声，所以必须对超声信号做进一步的分析和处理，以提高测量结果的准确性、可靠性和抗干扰性。文中主要结合相关法和插值法对超声信号进行处理，以得到准确的传播时间，实现对构件应力的测量。

1　超声应力测量原理

研究表明，在对应力敏感的几种超声波型中，临界折射纵波是测量构件应力最有效的波型之一[2]，笔者采用临界折射纵波测量构件应力。为尽可能避免由电气延时导致的测量误差，探头布置采用一发两收的形式。被测构件任一位置的超声波速是由其负载应力、残余应力、织构以及温度所决定的，当两个接收探头的间距固定时，超声波在构件表面的传播时间差正比于波速[3]。实际测量时，通常假设其负载应力大小为零，且忽略材料织构对传播时间的影响，则有：

ΔtRS=t-t*-ΔtT

(1)

式中：ΔtRS为由于残余应力作用导致的传播时间变化；t为实际测得的传播时间；t*为在理想条件下的传播时间；ΔtT为由实际温度与标准温度的偏差导致的传播时间变化。

根据临界折射纵波传播时间变化量与单轴应力值的关系[4]，则有：

(2)

式中：σ为实际构件中的应力值；E为弹性模量；L为临界折射纵波的声弹常数。

由于理想条件下的传播时间t*不易获得，通常是将退火后的构件作为零应力试样，即此时的构件应力σ0=0，则有：

t0-t*-ΔtT=0

(3)

所以：

t0=t*+ΔtT

(4)

将式(4)带入式(2)，由于E，L和t*均为常数，则有：

(5)

此时，σ为实际构件相对于零应力构件的应力变化量，在实际测量中用这一变化量描述构件中的应力值；Δt为实际构件相对于零应力构件的传播时间的变化量。超声波的应力常数K可以通过标定获得，所以只要测得Δt，即可获知构件中的应力值。

2　相关法在超声应力测量中的应用

测量超声波在构件内的传播时间时，通常采用峰值法、过零法、相关法和最小均方自适应时延估计法等，其中相关法作为一种经典算法，具有抵御噪声能力强、计算量适中等优点，很多工业过程和科学研究中都采用相关法测量延时。

在超声应力测量过程中，临界折射纵波沿构件表面传播一段距离后，分别由一前一后两个探头接收到，两探头所接收的超声信号间具有延时关系，如图1所示。可以利用相关函数在该延时值处取得最大值的特性，测量出该延时值的大小，即超声波在构件内的传播时间。

2．1传统相关运算方法

针对施加一定负载的被测构件，假设由前探头接收的超声信号为W1(n)，后探头接收到的超声信号为W2(n)。可以看出临界折射纵波在传播的过程中发生了一定的衰减，但并不影响使用相关法进行计算的效果，可以利用累加平均的方法实现相关运算[5]，运算过程可表示为：

(6)

通过寻找出相关峰值所对应的时刻，得出所求传播时间为t.

同理，针对零应力构件，假设由前探头接收到的超声信号为W10(n)，后探头接收到的超声信号为W20(n)，这时有：

(7)

得出峰值所对应的传播时间t0。

根据式(5)，可求得σ=KΔt=K(t-t0)。

2．2改进的相关运算方法

在实际测量时发现，由于两个接收探头的中心频率差异无法消除，将会导致两者的接收波形频率的不同，进而使得两者之间的相关性变差，将会给传播时间的测量结果带来误差。因此，提出用另一种计算方法来避开该误差。试验表面，同一接收探头在两次测量过程中所接收的波型同样也具有相关性，而且由于中心频率不变，对这两个波形进行相关运算，避免了引入附加的误差。

采用与式(6)同样的运算过程，得出W10(n)和W20(n)之间的时间间隔t1，以及W20(n)和W2(n)之间的时间间隔t2。如图2所示，不难理解Δt=t2-t1=t-t0，此时σ=KΔt=K(t2-t1)。

图2　改进的相关运算方法测量示意图

3　插值法提高测量精度

在利用相关法计算传播时间时，峰值所对应的时间轴上的点即为所求时间值，根据相关运算的理论，传播时间的计算精度只能精确到信号采集电路的采样周期。实际上，构件表面应力所引起的传播时间的改变是ns级的，如果采用100 MSPS的信号采集电路，也仅能精确到10 ns，这样的精度远不能满足实际工程应用中的要求。虽然采用更高速的信号采集电路可以提高测量的精度，但是随着采样率的提高，电路设计的成本也随之提高，而且需要处理的数据量也成倍增长，另外，信号采集电路对现场噪声也变得更加敏感。所以，应当在采样率保持不变的情况下，通过其他合理的手段提高测量的精度。在工程应用中，通常采用峰值插值法或峰值细化法[6-7]，后者是对时域插值法的改进，通过频域变换提高计算精度，但是运算量大，且算法繁琐，所以文中仍然讨论峰值插值法。常用的插值算法有线性插值、拉格朗日多项式插值、三次样条插值等。而针对峰值的插值多选用抛物线插值法，属于拉格朗日多项式插值的一种特殊情况。

图3　抛物线插值求相关峰值示意图

有下列方程组：

(8)

因此，插值后的结果为：

(9)

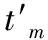
4　试验与测量结果分析

为了说明相关峰值插值法的计算效果，根据临界折射纵波应力测量原理，设计了超声应力测量系统，系统结构如图4所示。计算机接收到高速数据采集卡上传的超声信号数据后进行分析，高速数据采集卡采用100 MSPS高速数据采集卡NI5112。

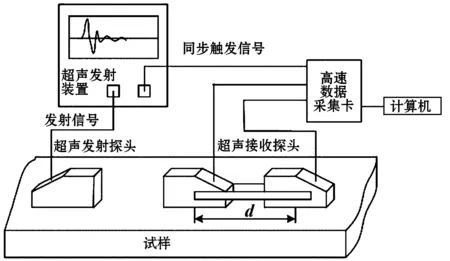
图4　超声应力测量系统

试验首先对构件超声波应力常数进行标定，利用加载系统和超声应力测量系统对厚度为22 mm的5%Cr钢构件进行表面应力测量，试验采用的超声探头为1 MHz．对获取的数据分别采用传统相关运算方法和改进的相关运算方法进行处理，绘出5%Cr钢构件表面应力与传播时间的变化量的关系如图5所示。图5中方点虚线为传统相关运算方法得出的计算结果，显然测量值的线性度较差；而三角点实线为改进相关运算方法后得出的计算效果，相比前者，测量值的线性度有明显的提高。

两种情况下，表面应力与传播时间具有明显的对应关系，再次验证了式(5)的正确性。对比两种运算方法，改进的相关运算方法的计算精度要高于传统的相关运算。根据改进的相关运算方法得到的测量值，可得到5%Cr钢构件的超声应力常数标定结果为K=5.78 MPa/ns．

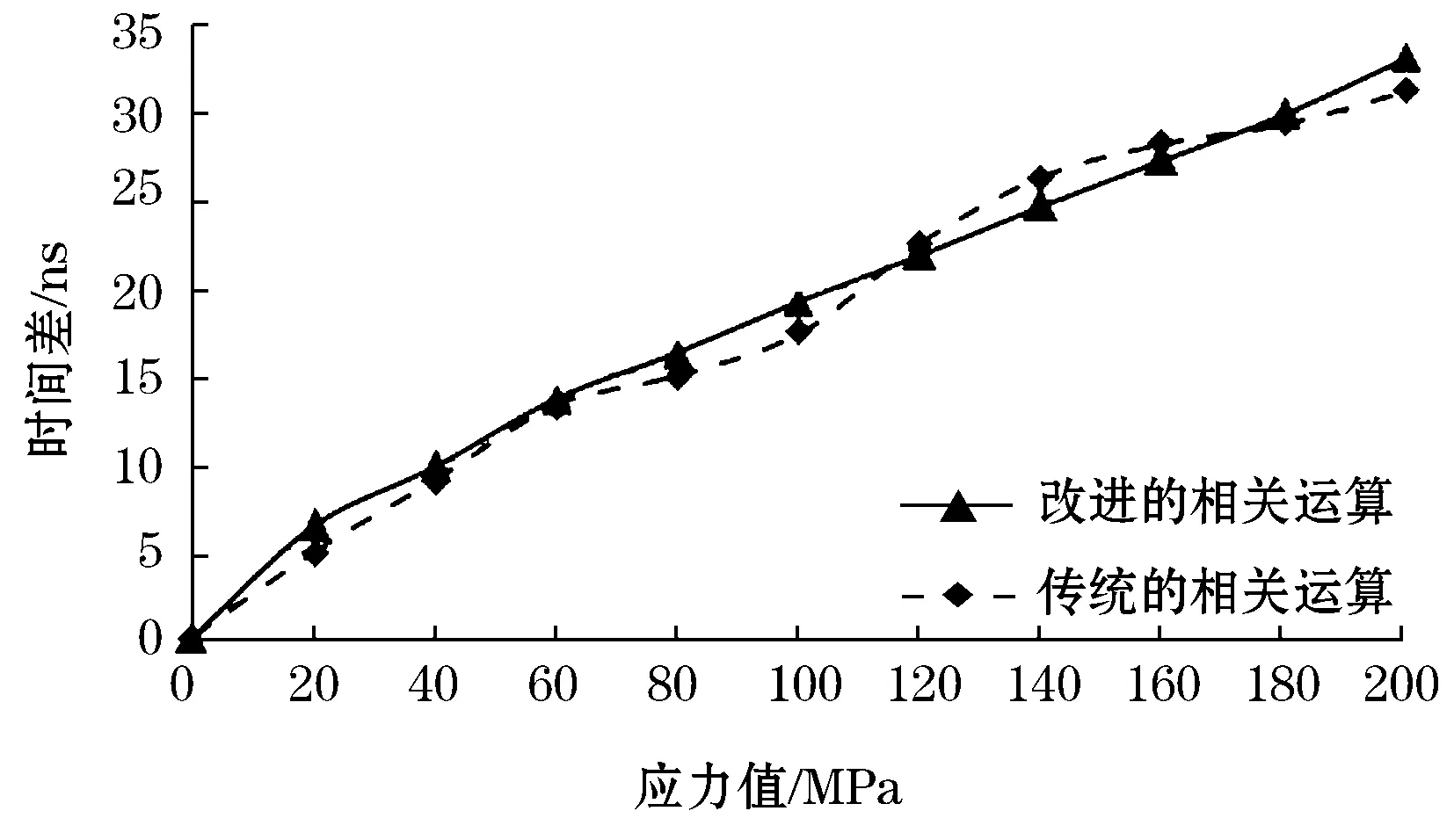
图5　5%Cr钢表面应力与时间差的关系

5　结论

运用临界折射纵波的理论，设计了基于相关峰值插值法的超声应力测量系统，并对5%Cr钢构件进行超声应力测量。通过试验分析，验证相关峰值插值法确实能有效提高测量的精度；通过对比两种相关运算方法，可以看出，使用改进的相关运算方法获得测量值的线性度有明显的改善，为进一步提高超声应力测量精度提供了一定的参考。

参考文献：

[1]ROSSINI N S，DASSISTI M，BENYOUNIS K Y，et al．Methods of measuring residual stresses in components．Materials and Design，2012，35：572-588．

[2]BRAY D E，TANG W．Subsurface stress evaluation in steel plates and bars using the LCR ultrasonic wave．Nuclear Engineering and Design，2001，207(2)：231-240．

[3]华云松，孙大乐，范群，等．基于临界折射纵波的超声波应力测量方法．无损检测，2008，30(9)：613-616．

[4]BRAY D E，JUNGHANS P．Application of the LCR ultrasonic technique for evaluation of post-weld heat treatment in steel plates．NDT&E International，1995，28(4)：235-242．

[5]高晋占．微弱信号检测．2版．北京：清华大学出版社，2011：258．

[6]杨亦春，马驰州，李晓东，等．相关峰细化的精确时延估计快速算法研究．声学学报，2003，28(2)：159-166．

[7]张学森，冯海泓，黄敏燕，等．两步法提高时延差估计精度的分析和实验验证．声学学报，2013，38(2)：153-159．