基于RBF神经网络的检定炉温度控制系统

冯冬青，李现旗

(郑州大学电气工程学院，河南郑州　450001)

0　引言

对检定炉的温度控制是高温热电偶检定过程中的核心部分[1]。当前使用的控温方法主要有前馈PID控制、模糊控制以及基于模型的预测控制[2-5]。文献[6]介绍了拟合模型参数辨识算法在温控电热系统中的应用，对温度系统的控制具有一定的参考意义。文献[7-8]详细阐述了神经网络在非线性系统控制中的应用，并用仿真结果验证了神经网络在非线性系统模型辨识以及控制中的优良特性。上述控制算法中，PID控制虽然简单易行但是完成多组温度点的整定需要多组控制参数；基于模糊控制的算法对模糊规则要求较高，而模糊规则的制定在很大程度上依赖于成熟的经验，一般人员很难在短时间内设计控制性能良好的模糊规则；基于模型的控制算法对系统模型的准确性要求很高，一旦模型失配，将会对系统硬件造成不可预估的损坏。文中研究了基于RBF神经网络整定PID控制算法在检定炉温度控制系统中的应用，经试验验证，该方法不但提高了检定炉的控温精度而且避免了设计过程中对控制经验和系统模型的依赖，实现了检定炉温度控制系统的高稳定性和高安全性。

1　检定炉温度控制对象分析

检定炉主要由外壳、保温层、加热元件、炉膛四部分组成。文中所述的检定炉为廉金属偶炉(炉长600 mm，孔径40 mm)。廉金属偶炉的炉膛一般是由陶瓷材料做成，陶瓷材料属于热的不良导体。炉膛与电阻丝之间热量传导的介质是空气，而空气也属于热的不良导体，所以检定炉内部的热量传导方式不能简单的用线性系统理论来描述。根据热力学定律，廉金属偶炉的温度变化主要与其热容量、加热量、散热量有关。当保温层确定时，炉温越高其散热量越大，从而对维持某一特定温度所需的加热量越大。环境温度的波动影响着散热量的变化，从而引起炉温的波动，进而给控制廉金属偶炉的温度稳定性带来了一定的难度。目前国产检定炉的降温方法采用自然降温法，导致了检定炉升温和降温过程中模型的不一致，对常规PID控制器和模糊规则的泛化能力提出了很高的要求。在升温(降温)过程中，检定炉温度系统的状态信息具有时变性，增加了控制难度。即使在室温、无空气对流的环境下，采用常规PID调节也很难获得良好的控制效果。模糊控制对模型对称的系统具有良好的控制能力和一定的泛化能力，但是对时变系统的控制不易取得良好的效果。基于模型的控制方法在廉金属偶炉使用初期有较好的控制效果，但是当模型失配时控制效果变差，需要再次进行模型辨识，并且有可能造成炉体损坏或者其他不良后果。综合上述分析，廉金属偶炉属于全局非线性、纯滞后、时变系统，常规的控制方法在实际应用中不能得到很好的效果。所以研究基于RBF神经网络的检定炉温度智能控制算法对提高检定炉温度控制精度具有一定的意义。

2　RBF神经网络辨识算法研究

2．1RBF神经网络结构

RBF神经网络是在20世纪80年代末提出的，它是一种具有单隐层的前馈网络。其中输入层到隐层是非线性映射，隐层到输出层是线性映射。这样的结构加快了RBF神经网络的学习速度并且避免了BP神经网络的局部极小问题。已证明RBF神经网络能以任意精度逼近任意连续函数。

RBF神经网络的结构如图1所示，其输入层3个节点，隐层4个节点，输出层1个节点。其中x1，x2，x3为网络输入层节点，φ1，φ2，φ3，φ4为网络隐层节点，ym是网络输出层节点。θj=[θji，…θji，…，θmn]T是网络隐层第j个接点的中心矢量，其中j=1，2，…，m，i=1，2，…，n．δ=[δ1，δ2，…，δm]T为网络隐层的基宽向量，δj为网络隐层第j个节点的基宽度，且为大于零的数。RBF神经网路隐层的激励函数采用高斯基函数，其中

图1　RBF神经网络结构

2．2被控对象的输入、输出模型在线辨识算法

RBF神经网络隐层节点到输出节点的输出权向量W=[w1，w2，…，wm]T。输出节点

(1)

RBF神经网络跟踪指标采用

(2)

根据梯度下降法搜索输出权值、节点中心以及节点宽度的最优值，由式(1)、式(2)可得

(3)

(4)

(5)

式中：i=1，2，…，n；j=1，2，…，m．

则输出权值wj、节点中心θj以及节点基宽δj的迭代算法如式(6)、式(7)、式(8)所示

wj(k)=wj(k-1)+ηω(yout-ym)φj+α〔wj(k-1)-

wj(k-2)〕

(6)

α[δj(k-1)-δj(k-2)]

(7)

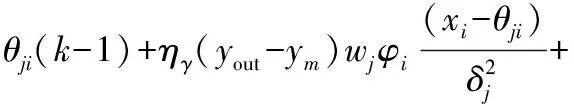
α〔θji(k-1)-θji(k-2)〕

(8)

式中：ηα、ηγ为各自的学习速率；α为动量因子。

系统的输入、输出辨识结果为

(9)

3　PID参数智能整定算法研究

为了减少误动作对检定炉温度的影响，采用增量式PID算法调节电阻丝的通电时间。增量式PID控制量计算方法如式(10)、式(11)所示

Δu=Kp·〔Err(k)-Err(k-1)〕+Ki·Err(k)+

Kd·〔Err(k)-2·Err(k-1)+Err(k-2)〕

(10)

u(k)=Δu+u(k-1)

(11)

式中：Err为温度控制误差，Err=T0-T1；T0为设定温度值，℃；T1为检定炉当前温度值，℃．

RBF神经网络整定PID参数采用误差最小准则，整定指标

(12)

增量式PID控制器的输入参数

xc(1)=Err(k)-Err(k+1)

(13)

xc(2)=Err(k)

(14)

xc(3)=Err(k)-2Err(k+1)+Err(k+2)

(15)

经计算，控制器的控制输出

u(k)=u(k-1)+Kp·xc(1)+Ki·xc(2)+Kd·xc(3)

(16)

根据误差最小准则，利用梯度下降法，算得Kp、Ki、Kd的整定算法如式(17)、式(18)、式(19)所示

(17)

(18)

(19)

式中εp、εi、εd为各自的学习速率。

RBF神经网络整定PID控制器控制检定炉温度系统框图如图3所示。

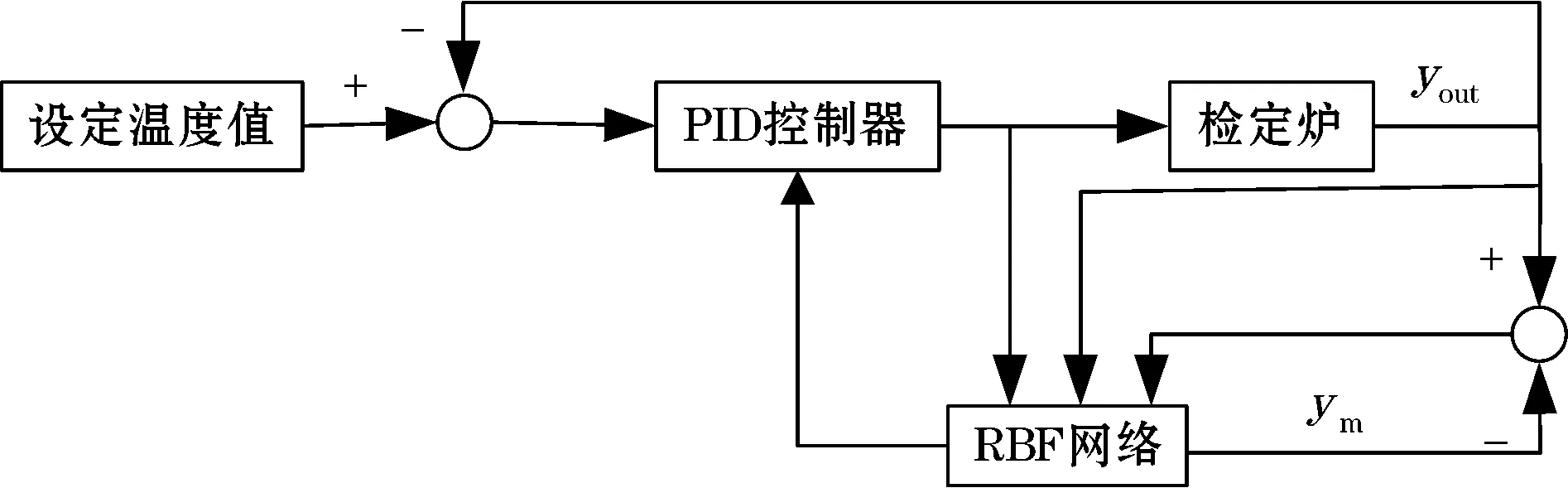
图3　RBF神经网络控制系统框图

4　系统设计及控制效果分析

4．1检定炉温度控制系统设计

检定炉温度控制系统结构如图4所示，下位机控制芯片采用C8051F020单片机(以下简称下位机控制器)，工业控制计算机与下位机控制器之间采用RS-485半双工通信方式通信，数据传输协议采用Modbus协议。工业控制计算机与数字电压表之间采用RS-232半双工通信方式通信。数字电压表采集标准偶(被检偶)的电压值供工业控制计算机查询，数字电压表转换时间200 ms．基于RBF神经网络的控制算法集成于上位机软件中，其根据RBF神经网络输入计算固态继电器保持导通状态的占空比，从而控制电阻丝的通电状态。当标准偶的温度达到鉴定标准要求的指标时下位机控制器启动自动切换端子，数字电压表采集被检偶的温度，温度检测完成后切换端子恢复到原状态，检定系统进行下一个温度点的整定。DS18B20温度传感器用于环境温度补偿。自动切换端子切换时间0．2 ms，固态继电器开关周期10 ms．

图4　检定炉控制系统框图

4．2控制效果及分析

检定炉温度控制系统的RBF神经网络输入层有4个节点u、yout(k)、yout(k-1)以及Err(k-1)，隐层有10个节点，输出层1个节点。输出权值的初值

wj=0.02·j，j=1，2，…，10

隐层节点中心的初值

θj=[0.1，0.2，0.3，0.4]，j=1，2，…，10

隐层节点高斯基函数的基宽向量初值

δ=[1，2，3，4，5，6，7，8，9，10]T·0.001

输出权值、节点基宽、节点中心的学习速率ηα=0．19、ηβ=0．16、ηγ=0．18，动量因子α=0．85。Kp、Ki、Kd的初值分别为180，5，30，学习速率初值分别为εp=0．5、εi=0．01、εd=0．01。

RBF神经网络温度跟踪指标曲线如图5所示。从图中可以看出，RBF神经网络控制器的跟踪速度特别快，在第7 s时能把跟踪指标缩小到1，在15 s时跟踪指标达到10-5精度。RBF神经网络跟踪的快速性为其辨识检定炉输入、输出关系提供了可靠的依据。

图5　RBF神经网络跟踪指标曲线

常规PID控温曲线如图6所示。从图中可以看出，控制曲线具有调节时间长、温度波动度大的特点，发生这种现象的原因主要是检定炉属于非线性、时变系统，常规PID控制器的参数不能自适应变化。此外，同一组PID参数只能在试验温度点的小范围(T0±50 ℃)内实现有效调节，不能对整个行程的所有温度点进行整定。

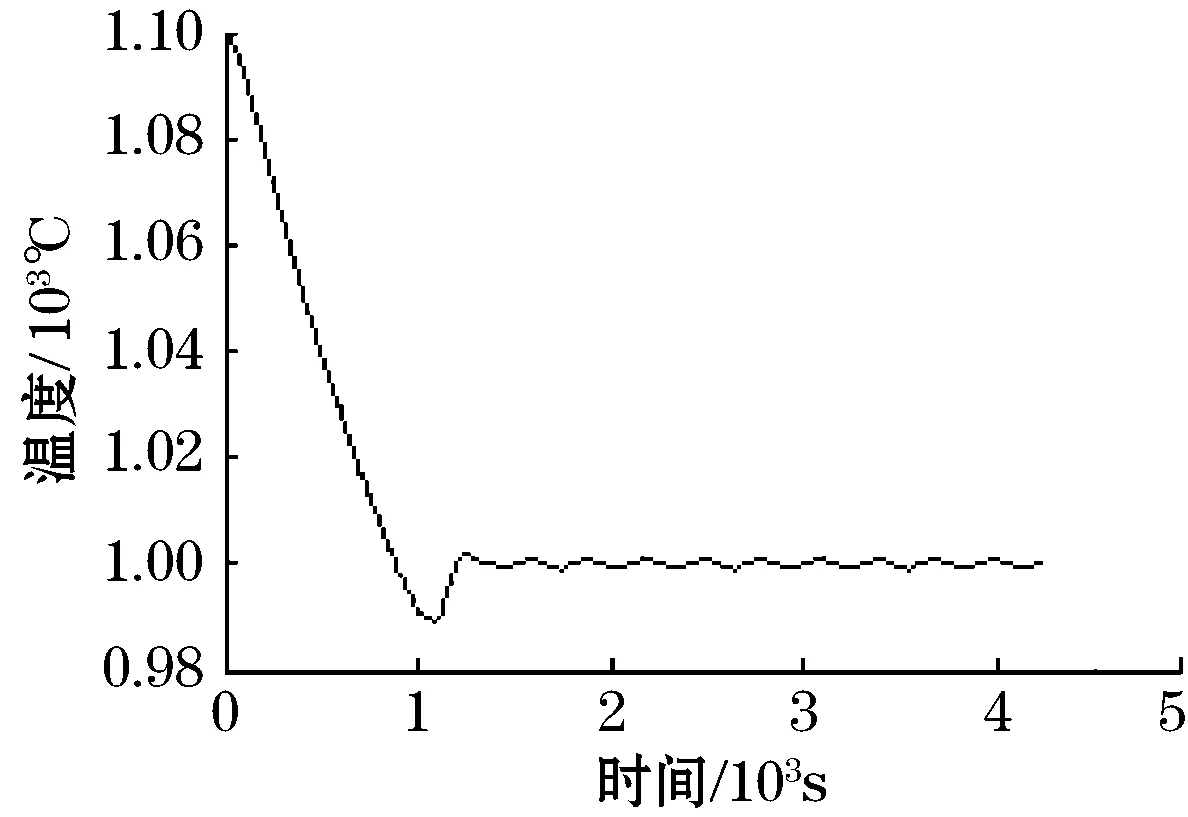
图6　常规PID控制器控温曲线

基于RBF神经网络的控制器控温曲线如图7所示，控温曲线具有调节时间短、稳态误差小、波动度小的特点。对比图6和图7，可以看出后者的温度拐点比前者的温度拐点提前了200 s，控温曲线的稳态误差可以控制在±0．25 ℃以内，温度波动度控制在0．2 ℃/min以内，提高了热电偶校验的准确性。

图7　RBF神经网络自整定控制器控温曲线

5　结束语

综上所述，采用RBF神经网络不仅可以实现检定炉系统输入、输出关系的快速有效辨识，而且还可以利用其自学习功能调节PID控制器参数以适应系统的变化，从而改善控制性能。

经过大量的试验，得知RBF神经网络隐层节点数目、PID参数自整定算法对控制性能具有很大的影响。隐层节点越多RBF神经网络越容易逼近检定炉温度变化曲线，但是会带来计算量的增加。不同的PID参数寻优算法在控制中有不同的控制效果，选择一种具有全局寻优能力的寻优算法更利于PID参数的自整定。

参考文献：

[1]JJF 1184—2007热电偶检定炉温度场测试技术规范．

[2]梁菲玲，赖华，汤占军，等．热电偶自动检定系统的炉温控制策略初探．云南大学学报(自然科学版)，2009，31(S2)：143-144．

[3]郭颖，吕剑虹，吴波，等．基于TS模糊模型的热工过程建模方法．系统仿真学报．2010，22(1)：210-212．

[4]刘成超，刘会兵，段宁．管式热电偶检定炉温控系统的设计．装备制造技术，2010(9)：58-59．

[5]冯冬青，张希平．基于神经网络的自学习模糊控制．郑州大学学报(工学版)．2003，24(4)：6-7．

[6]周杭挺，许力．基于神经网络的系统建模研究．工业控制计算机，2012，25(1)：63-64．

[7]和丽清，孙先仿，邱红专．非线性系统的结构选择及其参数的集员辨识．北京航空航天大学学报，2010，36(10)：1190-1191．

[8]冯冬青，孔祥伟，许仿．城市恒压变频供水系统的一种智能优化控制策略．郑州大学学报(工学版)，2011，32(1)：85-87．