串联电容对MEMS扭转微镜吸合角的影响

罗　伟，杨国珂，叶坤涛

(江西理工大学理学院，江西赣州　341000)

0　引言

随着微机电系统(MEMS)技术发展[1]，静电力驱动的扭转微镜逐渐广泛应用于投影显示[2]、 光谱仪[3]、现代光通信[4]等方面。从上世纪八十年代末开始，研究人员开展了对静电力驱动的扭转微镜的制作工艺、运动特性以及应用等方面的研究，发现了吸合效应，并利用物理模型对其吸合角进行了深入研究。

对静电力驱动的扭转微镜吸合角的理论分析主要是通过确定极间电场的静电力矩与机械回复力矩之间的平衡关系来进行的[5-9]。其中采用的静电力矩的计算方法有2种，一种是通过力矩的定义用微元法求解[5-7]，另一种是采用虚功原理，通过扭转微镜的极间静电能和静电力矩的关系来求解[8-9]。

O．Degani[5]在1998年建立了吸合电压与吸合角计算的物理模型，发现吸合角、吸合电压，与弹簧弹性系数无关，只与扭转微镜的结构参数有关；1999年，G．J．Su[6]对不同极板间距的微镜，分析了其驱动电压与偏转角度的关系，发现改变极板间距可以改变扭转微镜的吸合角，结论与文献5相符；2001年，X．M．Zhang[7]通过求解驱动电压与偏转角度的关系式的极值点，数值计算扭转微镜的吸合角，发现计算的吸合角只与电极尺寸有关，数据与实验相符；2002年D．Hah[8]以及2006年G．C．Zhu[9]的研究表明，扭转微镜的吸合角由极间电容与偏转角的关系决定，而与弹簧的弹性系数、驱动电压无关；而极板间电容与偏转角的关系只与该器件的几何结构有关。

上述研究都关注了影响扭转微镜吸合角的尺寸因素，都发现如果扭转微镜的几何尺寸确定，扭转微镜的吸合角就确定。而吸合角是扭转微镜在使用过程中可偏转的最大角度，它确定了扭转微镜的使用范围，是扭转微镜的一个重要性能指标[5-9]。目前，技术人员主要是通过改变扭转微镜的几何结构来调整这一角度，以满足实际需要。

1997年，J．I．Seeger[10-11]曾提出通过给平行板静电驱动器串联一个电容，引入电容负反馈的方式，来改善平行板静电驱动器的系统稳定性和加大驱动距离，且2000年，E．K．Chan[12]更深入地研究了串联电容对平行板静电驱动器的影响。受此启发，该研究对扭转微镜在串接电容后，其吸合角的变化进行了仿真分析。并且对仿真结果进行了理论上的解释。研究表明，引入串接电容后，扭转微镜的吸合角增大，系统稳定性提高，扩展了固定尺寸扭转微镜的转角范围。

1　MEMS扭转微镜的吸合角

静电力驱动的扭转微镜结构的三维示意图，如图1所示。扭转微镜由微镜面、悬臂梁(扭转梁)和基底构成。 当给扭转微镜系统施加某一恒定的驱动电压后，扭转微镜在静电力的作用下发生扭转，同时扭转微镜由于扭转而产生形变，当极间电场产生的静电力矩T与形变产生的机械回复力矩Tm满足式(1)时，扭转微镜理论上在某个偏转角度处达到力学平衡态：

图1　扭转微镜结构的三维示意图[13]

(1)

基于MEMS扭转微镜的静态特性的大角度模型分析理论，在只考虑极板间电场的情况下，由微元法求解的扭转微镜静电力矩T与机械回复力矩Tm分别如式(2)、式(3)所示[13，14]：

(2)

Tm=kθ

(3)

(4)

式中：LM、WM分别代表扭转微镜的镜面的长度与宽度；wB、tB、lB分别为扭转微镜悬臂梁的宽度、厚度和长度的一半；d为扭转微镜与基底的间距(见图1)；V为扭转微镜与基底之间的驱动电压；θ为扭转微镜的偏转角度；G为微镜悬臂梁材料的剪切模量；k为系数。

扭转微镜的具体尺寸如表1所示[13]，材料为多晶硅，其剪切模量G为69GPa[15]。

表1　扭转微镜的尺寸[13]　μm

通过式(3)、式(4)，可数值求解表1所示的微镜的机械回复力矩随偏转角度的变化曲线(见图2)，结果与驱动电压无关，是斜率为k的直线。

由式(2)，并给定不同驱动电压，可数值求解不同的静电力矩随偏转角度的变化曲线(见图2)。对表1所示微镜的数值计算表明，驱动电压为0～87.9 V时，如85 V，静电力矩曲线与机械回复力矩曲线有1个交点A1，为力学稳定平衡点；驱动电压为87.9～241 V时，如200 V，有2个交点A2、A3，分别为稳定平衡点与非稳定平衡点；驱动电压为241 V时，两类平衡点合并成切点，静电力矩曲线与机械回复力矩曲线相切，只有1个交点A4，为扭转微镜的吸合点[5，13]。与吸合点横坐标对应的偏转角度，即吸合角为31.8°，对应的驱动电压241 V为所谓的吸合电压；驱动电压大于241 V时，如320 V，静电力矩曲线与机械回复力矩曲线无交点，微镜处于非稳定状态。

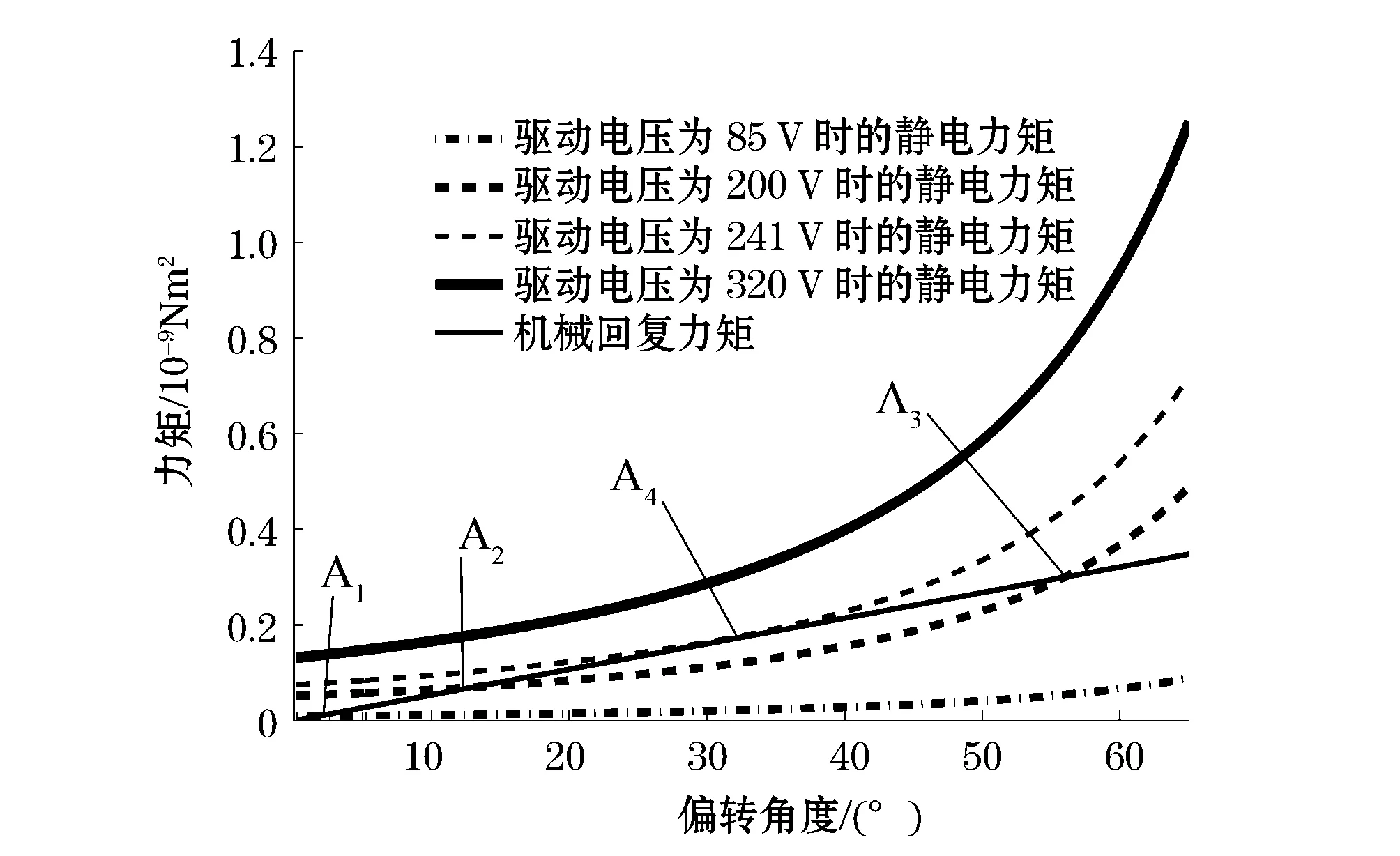
图2　机械回复力矩、不同驱动电压的静电力矩随偏转角变化的曲线

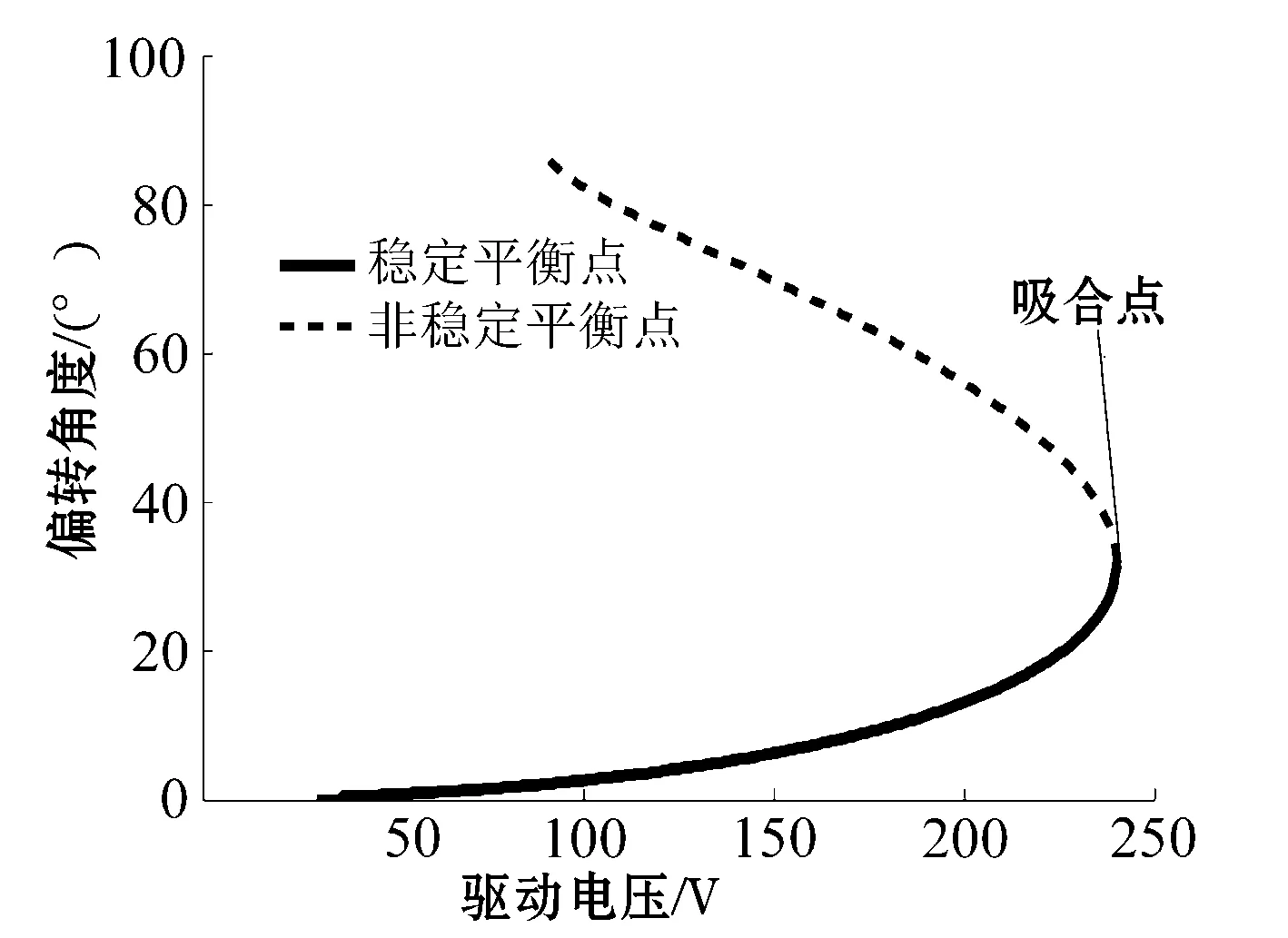
图3　扭转微镜驱动电压与偏转角的关系曲线

若取驱动电压范围0～241 V，电压值间隔为0.1 V，并将此过程中的静电力矩曲线与机械回复力矩曲线的所有平衡点对应的驱动电压为横轴，偏转角为纵轴，绘制成图，可得到扭转微镜的偏转角与驱动电压之间的关系曲线，见图3。

可以证明此计算过程中得到的吸合角只与微镜的尺寸参数有关，而与其他因素无关[8-9]。

2　串联恒定电容时微镜的吸合角

微镜可以等效为一可变电容C，表示的是图1中镜面与基底之间电容值。其随偏转角度的变化关系为[16]：

(5)

式中：LM、WM、d分别为扭转微镜的长度、宽度和镜面与基底之间的间距。

图4(a)表示的是扭转微镜驱动电路的等效电路示意图。图中电压V为无串联电容的驱动电压。为了改变扭转微镜的吸合角，在微镜驱动时串接一个恒定电容，驱动电路的等效电路如图4(b)所示，Vc是串联恒定电容Cf后的驱动电压。

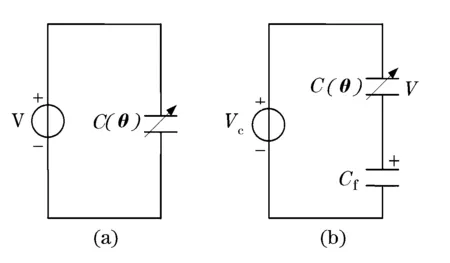
图4　微镜串联电容前后的的驱动电路示意图

串联恒定电容Cf后，扭转微镜与基底之间电压为V，和驱动电压Vc不同，由电容串联分压原理可知：

(6)

联立式(2)、式(6)得到串联电容后扭转微镜的静电力矩随角度的变化关系式(7)：

(7)

依次取驱动电压为50 V、100 V、150 V、200 V、250 V，分别计算串联电容前、后的扭转微镜静电力矩以及机械回复力矩随偏转角度的关系，结果如图5所示，其中串联电容Cf的值为0.04 pF．

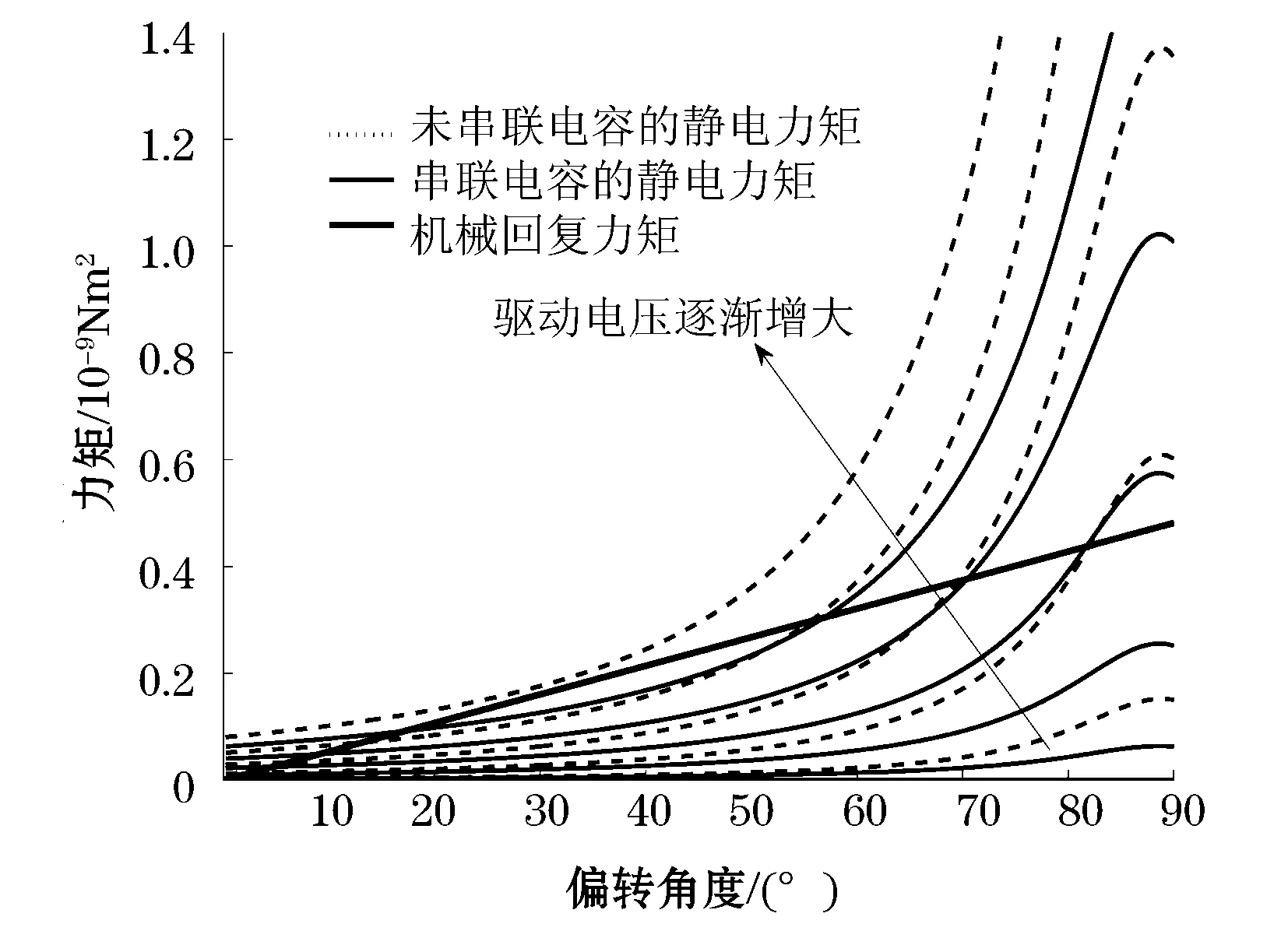
图5　串联电容后，静电力矩随偏转角变化曲线族的改变

图5中，虚线族代表的是串联电容前，微镜静电力矩随偏转角度的变化关系；实线族代表的是串联电容后，微镜静电力矩随偏转角度的变化关系；对同一曲线族，曲线的整体位置越高，对应的驱动电压越大。对同一驱动电压，串联电容后的静电力矩，相对于串联电容前的静电力矩曲线，整体向下移动；图中粗实线为微镜机械回复力矩随偏转角的变化关系。

采用类似于图3的绘制方法，将串联电容后不同驱动电压时，静电力矩与机械回复力矩曲线的所有交点对应的驱动电压为横轴，偏转角为纵轴，绘制成图，其中的驱动电压值从0开始，间隔为0.1 V，得到串联电容前后扭转微镜的偏转角与驱动电压之间的关系曲线(见图6)。图6显示，串联恒定电容Cf=0.04 pF后，扭转微镜的吸合角增大，由之前的31.8°变为串联电容后的35.2°，对应的驱动电压为285.5 V．

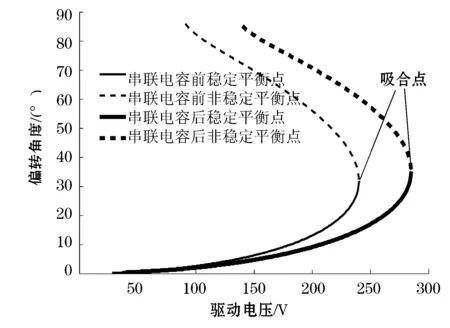
图6　串联电容前后，偏转角vs．驱动电压曲线的对比

微镜极板间的静电力矩随偏转角变化的关系，归根到底是由加上驱动电压后，极板上的电荷量随偏转角的变化关系决定的。由于串联电容的存在，极板上的电荷量随偏转角的变化关系发生改变，使得静电力矩随偏转角度增加的曲线族放缓，于是静电力矩曲线与机械回复力矩曲线的相切点，即吸合点也发生变化，吸合角也随之改变。

3　串联不同电容时微镜的吸合角

串联不同电容值的电容，吸合角将变化到不同数值。对串联不同电容值的电容的情况进行数值仿真计算，获得对应的不同吸合角，参见图7。图中曲线显示，当串联电容逐渐增大时，扭转微镜的吸合角逐渐减小，最终趋近于未加串联电容时的吸合角度31.8°；串联电容数值上接近0时，吸合角度值会接近63.8°；当串联电容值为0，即无串联电容时，吸合角为31.8°。

图7　串联不同值的电容与扭转微镜的吸合角的关系

由上述数值解可获得一般性结论，即串联电容后，微镜的吸合角度会增大；串联电容Cf趋向于无穷大时，加电容后的吸合角趋向于未加电容时的吸合角；串联电容变小，吸合角变大。此结论可以通过数学分析的方法证明，详细推导过程见附录A．

4　结束语

采用对比扭转微镜的静电力矩与机械回复力矩随角度的变化曲线的方法，来研究扭转微镜驱动电压与偏转角度的关系，并重点关注了微镜的吸合角。在J．I．Seeger[10-11]和E．K．Chan[12]研究平行板静电驱动器中引入串联电容的启发下，研究了在扭转微镜的驱动电路中，加入一个恒定的串联电容后，扭转微镜的吸合角的变化情况；并对加入不同串联电容值时，扭转微镜吸合角的变化规律进行了数值计算和解析分析。

与J．I．Seeger[10-11]和E．K．Chan[12]在平行板静电驱动器中引入串联电容，可加大平行板静电驱动器的驱动距离的结论类似，该研究结论表明：串联电容后，微镜的吸合角增大，提高了其稳定性；微镜的吸合角随着串联电容减小而逐渐增大。即在微镜几何尺寸固定的情况下，吸合角还可通过设计驱动电路来调整，这对扭转微镜在实际应用中，如何扩展其使用范围，提高稳定性，提供了新思路。

附录A：

未串联电容时，微镜的驱动电压与偏转角的关系可以表示成(A1)式[13][14]：

(A1)

式中：V(θ)是扭转微镜偏转角度θ对应的驱动电压值；A、B只与扭转微镜尺寸有关，若尺寸给定，它们为常数；f(θ)是关于偏转角度θ的函数，也只与扭转微镜尺寸有关：

A=εWMπ

(A2)

(A3)

(A4)

串联电容Cf后，联立式(6)、(A1)式，得到扭转微镜驱动电压与偏转角的关系式：

(A5)

微镜的驱动电压Vc随偏转转角的变化趋势的示意图如图8所示。

图8　偏转角度与驱动电压关系曲线示意图

理论上通过求解dVc/dθ=0可得到图8中扭转微镜的吸合角[8]，即为图8中M点对应的偏转角；直接求解dVc/dθ=0来获得吸合角的解析表达式非常困难。运用数学分析的方法，可以对吸合角随串联电容值的变化的关系进行较好说明。

若将讨论区间设定在与吸合角对应的坐标点M附近，显然在某偏转角的位置上有dVc/dθ>0，则说明该偏转角小于吸合角，如图8中的N点；反之dVc/dθ<0，则说明该偏转角大于吸合角。

将(A1)式两边对θ求导令其为0，解得串联电容前，微镜的吸合角为θPI，则有：

(A6)

对(A5)求导得：

(A7)

若将原吸合角θPI代入(A7)式，结合(A6)式，有：

(A8)

所以：

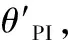
对(A8)取极限有：

(A9)

表明：Cf趋向于无穷大时，加电容后的吸合角趋向于未加电容时的吸合角θPI。

设串联电容为Cf1时，其吸合角为θCf1，有：

(A10)

若串联电容为Cf2(Cf2

(A11)

由(A11)、(A10)两式相减得：

(A12)

下面判断(A12)式左边的正负。

(A13)

(A14)

(A14)式代入(A12)式得：

(A15)

表明：在串联电容后的驱动电压随偏转角变化的曲线上，与原吸合角θCf1对应的位置的曲线斜率大于0，θCf1小于此时真正的吸合角θCf2，即串联电容值减小，吸合角增大。

参考文献：

[1]刘凯，陈志东，邹德福，等．MEMS传感器和智能传感器的发展．仪表技术与传感器，2007(9)：9-10．

[2]CHAN Y C，WONG C C，WANG C S，et al．Design and Fabrication of a MEMS scanning mirror with and without comb offset．5th IEEE International Conference on Nano/Micro Engineered and Molecular Systems，Xiameng，2010．

[3]KENDA A，SCHERF W，HAUSER R，et al．A compact spectrometer based on a micromachined torsional mirror device．The IEEE Sensors 2004，Vienna，Austria，2004．

[4]TOSHIYOSHI H，FUJITA H．Electrostatic micro torsion mirrors for an optical switch matrix．Journal of Microelectromechanical Systems，1996，5(4)：231-236

[5]DEGANI O，SOCHER E，LIPSON A，et al．Pull-In Study of an Electrostatic Torsion Microactuator．Journal of Microelectromechanical Systems，1998，7(4)：373-379

[6]SU G J，LEE S S，and WU M C．Optical scanners realized by surface-micromachined vertical torsion mirror．IEEE Photonics Technology Letters，1999，11(5)：587-589．

[7]ZHANG X M，CHAU F S，QUAN C，et al．A study of the static characteristics of a torsional micromirror．Sensors and Actuators，2001，90(1)：73-81．

[8]HAH D，Toshiyoshi H，WU M C．Design of electrostatic actuators for MOEMS applications．Conference on Design，Test，Integration，and Packaging of MEMS 2002，Cannes，France，2002．

[9]ZHU G，PACKIRIRSAMY M，HOSSEINI M，et al．Modelling and control of an electrostatically actuated torsional micromirror．Journal of Micromechanics and Microengineering，2006，16(A3)：2044-2052．

[10]SEEGR J I，CRARY S B．Stabilization of electrostatically actuated mechanical device．Proc．International Conf．on Solid State Sensors and Actuator，Chicago，1997．

[11]SEEGR J I，BOSER B E．Dynamic and control of parallel plate actuators beyond the electrostatic unstability．Proc．International Conference on Solid-State Sensors and Actuators，Japan，1999．

[12]CHAN E K，DUTTON R W．Electrostatic micromechanical actuators with extended range of travel．Journal of Microelectromechical Systems，2000，9(3)：321-328．

[13]BHASKAR A K，PACKIRISAMY M，BHAT R B．Modeling switching response of torsional micromirror for optical Microsystems．Mechanism and Machine Theory，2004，399(A5)：1399-1410．

[14]王振霖，陈学康，曹生珠．大角度扭转微镜的静态特性分析．科学技术与工程学报，2008，8(6)：4675-4676．

[15]SHARP W N，EBY M A，COLES G，．Effect of temperature on mechanical properties of polysilicon．The 11th International Conference on Solid-State Sensors and Actuators，Munich，Germany，2001．

[16]AGUDELO C G，Packirisamy M，ZHU G C．Nonlinear control of an electrostatic micromirror beyond pull-in with experimental validation．Journal of Micromechanical Systems，2009，18(4)：914-923．