平面S型微弹簧多轴向弹性系数分析

程建建，聂伟荣，周织建，黄庆武

(南京理工大学机械工程学院，江苏南京　210094)

0　引言

微弹簧是MEMS(micro electro-mechanical systems)器件的重要组成部分，其为MEMS器件提供弹性力以及传递能量[1]。S型弹簧是最典型微平面弹簧之一[2]，其3个坐标方向的弹簧弹性被广泛地应用于MEMS器件设计中。文献[3]采用S型弹簧的横向刚度为结构的主刚度，但缺少相应的弹性系数理论计算公式。文献[3-4]利用S型弹簧纵向弹性设计器件，文献[2，5]推导了集中力作用下S型弹簧的纵向弹性系数。文献[6-7]中结构的功能性刚度为S型弹簧的垂直方向刚度，文献[8]对集中力作用下S型弹簧垂直弹性系数进行了理论公式的推导。文中推导了集中力(即等效作用于弹簧自由端的质点力)作用下S型弹簧的横向刚度，修正了文献[8]弹性系数计算公式。在惯性环境作用下的弹簧质量系统中，影响弹簧弹性系数的结构参数类型及影响程度将发生改变，因此上述文献S型弹簧弹性系数公式不适用于微惯性开关、微加速度计等微惯性执行器件中弹性系数计算。文中分别推导了惯性力(即环境加速度作用于微弹簧质量系统而产生的力)作用下，平面S型弹簧横向、纵向以及垂直方向弹性系数理论计算公式。

1　弹簧结构参数

平面S型弹簧的结构，如图1所示。弹簧由n个结构相同的U型单元组成，质量块(其体积为Vem)与平面S型弹簧的第一个U型单元的顶端相连接，第n个U型单元底端固定。B为弹簧线宽，L为弹簧U型单元直梁长度，R为弹簧弯半径，H为结构厚度，L1为质量块质心到弹性单元U．1自由端的Y轴向长度。

图1　平面S型弹簧

2　弹簧弹性系数分析

集中力Fcx，Fcy，Fcz分别作用在U．1弹性单元的自由端，S型弹簧在横向(X轴向)、纵向(Y轴向)、垂直方向(Z轴向)分别产生相应线弹性形变。因此在线弹性范围内，利用力学能量法(卡尔第二定理)：

(1)

式中：Vε为应变能；Fi任一载荷；δi为Fi方向的位移量。

可求解任一U型单元Y轴方向的位移量δy

(2)

式中：My(x)为产生的δy力偶矩；Fei为载荷；I为U型弹簧单元的惯性矩，I=B3H/12。

S型平面弹簧U型弹簧单元柔度系数计算公式

(3)

包含n个U型单元平面S型弹簧的弹性系数计算公式

(4)

利用上述方法可以推导出在集中力Fcx作用下，S型弹簧X轴向柔度的理论计算公式

(5)

式中：E为材料的弹性模量；I为截面X、Y轴向惯性矩。

文献[4-5]已推导出Y轴向S型弹簧的弹性系数理论计算公式，理论值与仿真值得相对误差小于3%。文献[16]推导出了S型弹簧Z轴向的弹性系数理论计算公式，文中对文献[16]中的理论公式进行修正，推导出S型弹簧Z轴向的柔度系数理论计算公式

(6)

在微惯性传感器中，弹簧承受环境力为体积力，其所承受的载荷不可以忽略。因此上述在集中力作用下，S型弹簧的弹性系数计算公式不适用于微惯性器件中弹簧弹性系数计算。加速度ax、ay、az分别作用在弹簧-质量系统上，S型等宽弹簧产生线弹性形变，利用上述方法分别推导出弹簧X轴向柔度系数理论计算公式

(7)

式中

S型弹簧Y轴向柔度理论计算公式为

(8)

式中：Qy1=2L3+3πRL2+12R2L+3πR3/2；Qy2=15L4/48+2R2L2+πR3L/2+π2R4/16+7πRL3/12；ceil[(n-1)/2]为朝正无穷大方向取整。

S型弹簧Z轴向柔度理论计算公式为

(9)

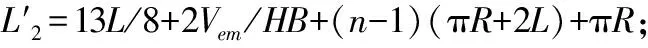
式中：

采用文献[10]估算UV-LIGA工艺电铸薄膜材料的杨氏模量方法，选取镍材料的弹性模量E=1.6×1011Pa，泊松比μ=0.312，材料密度ρ=8 910 kg/m3．利用仿真软件进行验证，S型弹簧验算结构参数B=20 μm，L=400 μm，R=100 μm，H=60 μm，Vem=6×105μm3，L1=65 μm，n=5。集中力Fcx=1 μN，Fcy=1 μN，Fcz=1 μN分别作用在U．1弹性单元的自由端，S型弹簧产生弹性形变，分别获得弹簧X、Y、Z轴向弹性系数理论值与仿真值，以及理论值与仿真值的相对误差，如表1所示。加速度ax=1 m/s2、ay=1 m/s2、az=1 m/s2分别作用在弹簧-质量系统，即可得弹簧在惯性环境下，S型弹簧X、Y、Z轴向弹性系数理论值与仿真值，以及理论值与仿真值的相对误差，如表1所示。

表1　S型弹簧弹性系数K分析

从表1分析可知，S型弹簧分别在集中力下与惯性力环境下，X、Y、Z三轴向的弹性系数理论计算公式可信。同一根弹簧在两种不同环境下的相对应弹簧弹性系数不相等，因此集中力环境下的弹簧的弹性系数理论计算公式不适用于微惯性器件中。两种环境下，X轴向弹性系数Kx最小，其次为Z轴向的弹性系数Kz，Y轴向的弹性系数Ky最大。

从图2可知，S型弹簧的弹性系数分别与两种环境力成反比关系(Kx．F|Fcx=+∞=0，Kx．F|Fcx=0=3.39 N/m，Kx．a|a=+∞=0，Kx．a|a=0=7.84 N/m．因此无环境力作用下，弹簧的X轴向的刚度最大(与弹簧的结构参数相关)。弹簧在X轴向高冲击力作用下，弹簧刚度近似为零，增加了齿形延时机构在高载荷下延长时间，增强了结构对环境幅值的区分。

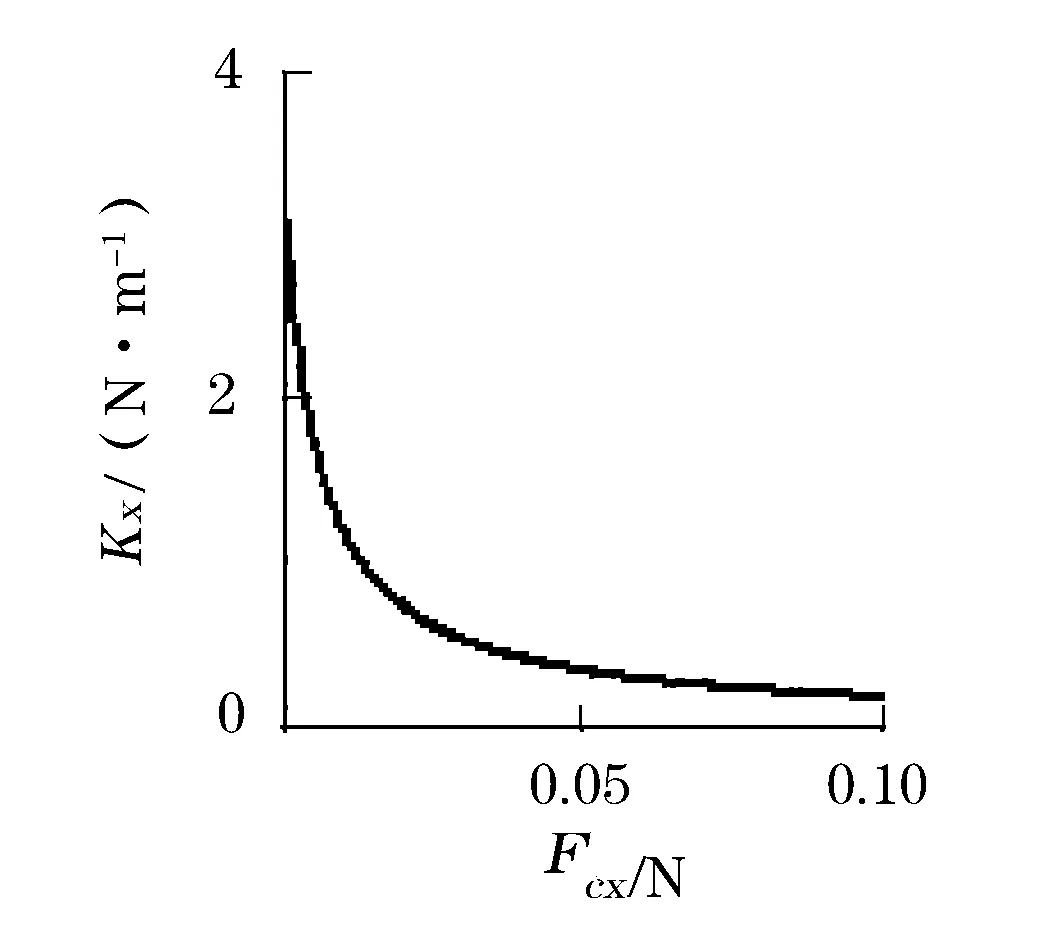
(a)集中力Fcx作用下

(b)加速度a作用下

在Y轴向惯性力作用下，等线宽微弹簧U型单元的最大正应力近似计算公式

σi=6aρ(L+R)[Vem/H+i(2L+πR)B]/B2

(10)

(a)U型单元Y轴向弹性系数

(b)U型单元近似最大应力

图3S型弹簧分别在两种环境力作用下U型弹性单元Y轴向弹性系数与在惯性力作用下U型单元近似最大应力

由图3(a)所示，在集中力作用下，S型弹簧任一U型弹性单元的弹性系数相等。在惯性力作用下，弹簧U型弹性单元的弹性系数与其在弹簧所处位置有关。与质量块链接的U型单元的弹性系数最大，与锚点相连的U型弹簧单元的弹性系数最小。 在惯性环境下，第U．n弹性单元的最大正应力大于其余弹性单元，第U．1弹性单元的最大正应力最小(如图3(b)所示)。在惯性力环境下，S型弹簧任一U型单元的承载能力不一致，影响了弹簧整体抗过载能力。

图4　弹簧在惯性力作用下质量块体积Vem对Z轴向弹性系数影响

由式(6)可知，S型弹簧在集中力作用下，弹簧弹性系数与质量块体积Vem无关。如图4所示，上述S型弹簧-质量系统结构参数质量块体积Vem改变，弹簧结构参数不变。在惯性环境下，弹簧的Z轴向弹性系数随着质量块体积Vem的增大而减小。Vem接近无穷大时，Z轴向的弹性系数Kz趋近于常数(值取决于弹簧结构参数)。利用弹簧的Z轴向刚度的微惯性开关，增大Vem，可减小弹簧Z轴向刚度，增加了电极之间的接触面积以及接触面积，开关性能充分发挥。

3　结束语

文中推导了集中力作用下，平面S型弹簧横向弹性系数理论计算公式，修正了文献[8]中弹簧垂直方向弹性系数计算公式；推导了在惯性环境下，S型弹簧横向、纵向以及垂直方向弹簧的弹性系数公式。利用仿真软件证明了理论公式的正确性以及在集中力与惯性力下弹簧弹性系数区别。通过分析横向环境力对弹簧横向弹性系数的影响，表明了弹簧横向弹性系数随横向环境力增大而减小；分析弹簧在纵向惯性力作用下U型弹性单元纵向弹性系数与其最大正应力，表明了在惯性环境下与锚点相连弹簧U单元弹性系数最小以及最大正应力最大；分析了在垂直方向惯性力作用下，质量块体积对弹簧垂直方向弹性系数影响，表明了弹簧弹性系数随质量块体积增大而减小。为微惯性器件的优化设计提供了一定的理论依据。

参考文献：

[1]何光，石庚辰．MEMS弹簧特性的有限元分析．微计算机信息，2006，22(2)：158-160．

[2]吴志亮，常娟，冯鹏洲，等．引信用MEMS平面微弹簧弹性系数分析．南京理工大学学报，自然科学版，2008，32(2)：140-143．

[3]何光，石庚辰．平面S型与平面W型MEMS弹簧性能比较研究．传感技术学报，2008，21(2)：288-291．

[4]刘小岗，施坤林，牛兰杰，等．有限元法在MEMS安全系统仿真中的应用．探测与控制学报，2006，28(1)：14-16．

[5]SLICKER J M．MEMS latching high power switch：USA，7893799B1[P]，2011-02-22．

[6]YANG Z Q，CAI H G，DING G F，et al．Dynamic simulation of a contact-enhanced MEMS inertial switch in simulink．Microsyst Technol，2011，17：1329-1342．

[7]LIU H C，LEE C K，KOBAYASHI T，et al．A new S-shaped MEMS PZT cantilever for energy harvesting from low frequency vibrations below 30 Hz．Microsyst Technol，2012，18：497-506．

[8]李晓杰，牛兰杰，翟蓉，等．S型MEMS平面微弹簧垂直弹性系数．探测与控制学报，2010，32(1)：57-60．

[9]刘士光，张涛．弹塑性力学基础理论．武汉：华中科技大学出版社．2008．

[10]张段芹．微构件拉伸测试技术及其力学性能研究：[学位论文]．大连：大连理工大学，2009．