基于主成分支持向量机的商品住宅价格预测——以郑州市商品住宅价格为例

张彦周

（河南职业技术学院 基础教学部，河南 郑州450046）

一、引言

商品住宅价格的预测是一个研究热点问题，国内有许多学者对此做了大量研究，如郭培俊的基于灰色理论的温州房价预测模型［1］，闫妍的基于TEL@I 方法论的房价预测方法［2］，谈萍的基于灰色马尔可夫模型的上海房价走势实证研究［3］，程松林的武汉市商品房均价的预测［4］。这些研究取得了一定的成果，但大多数研究只考虑了房价的时间变化趋势而忽视了影响房价的内在规律因素。

商品住宅价格是诸多因素共同作用的结果，这些影响因素分为两类，一类是房地产市场或房地产行业自身的因素，如固定资产投资、房地产开发投资、施工面积、竣工面积、当前商品住宅价格等；另一类是反映宏观经济环境的因素，如生产总值、人均可支配收入、消费者价格指数、居民储蓄等。20世纪60年代，Vapnik及其同事提出的统计学习理论被认为是目前针对小样本统计估计和预测学习的最佳理论［5］。由于支持向量机算法是一个凸优化问题，因此局部最优解一定是全局最优解。这些特点是其他学习算法，如神经网络学习算法所不及的［6］。近几年，支持向量机方法在非线性系统辨识、预测预报、建模与控制等方面被广泛应用。笔者结合郑州市2004年到2012年的统计数据，以季度为单位，给出10个与商品住宅价格相关的影响因素，利用主成分分析，对数据样本进行降维处理，然后利用支持向量机进行学习预测，给出房价预测数学模型，预测结果表明该方法准确率高，简单实用。

二、商品住宅均价预测

1.指标选取与数据来源。商品住宅价格的变化受多种因素的制约，并且各种因素的影响程度也有很大差别，其中，宏观经济的基本因素及其波动是影响商品住宅价格波动的主要原因。在研究过程中发现，由于宏观经济指标数据样本时段的选取存在一定的主观性和片面性，因此实证结果也存在着较大的差异。因此，结合我国房地产市场的发展现状，分析选用合适的宏观经济指标及一定的房地产自身微观指标作为标准，选取以下10种因素作为影响房价的主要指标。第一，固定资产投资。固定资产投资和房地产业规模一般成正相关。投资与房地产行业的相关程度越高，对房地产行业的发展刺激作用就越大，反之，相关程度越低。第二，房地产开发投资。适当的房地产开发投资会保障房地产行业的健康发展。投资水平过高会刺激房地产迅速发展。但房地产价格超过合理水平，房地产投资者获得超额利润时，便会出现房地产投资“过热”的现象，从而酝酿巨大风险；反之，降低投资水平会限制房地产行业的发展。所以适当的房地产开发投资对房地产行业的可持续发展是十分重要的。第三，开工房屋的施工面积。这种影响具有延时性和反作用性。延时性指开工房屋的施工面积代表了未来的市场供给能力，对房价有较大的影响；反作用性是指现阶段的房价也会进一步影响开发商对商品住宅的开发程度。第四，房屋竣工面积。房屋竣工面积代表了当下房地产的供给。在市场经济条件下，房屋竣工面积对房价有直接的影响，随着竣工面积的增加，房价将会有下降的趋势。第五，商品房销售面积。房屋销售面积代表了现阶段房地产供需市场的冷热程度，它与房价存在某种特定的关系，会间接影响未来的房价。第六，国民生产总值。GDP 从某种程度上反映了一个国家的整体经济水平。当经济增长较快时，就业人口和城市人口不断增加，从而带动住宅需求增加，商品住宅价格会快速上涨。房价上涨，房地产投资增加，从而拉动经济快速增长。近十年来我国经济一直处于快速发展阶段，GDP 增速平均保持在8.6%以上，而同期房价也在快速增长，涨幅甚至超过了GDP的涨幅。因此，作为反映整体宏观经济发展水平和房地产行业发展背景的GDP，与房地产价格之间必定存在着相关性。第七，人均可支配收入。人均可支配收入决定住房的有效需求，是影响住宅价格水平的一个重要因素。收入增加会提高居民购房的支付能力，从而增加住房需求，促使房价上涨。第八，消费者物价指数。现阶段我国没有把房地产价格指数统计到居民消费物价指数中，但是消费物价指数反映整体国民经济的通胀程度，也间接反映了房地产市场的运行状况。第九，居民储蓄额。居民储蓄额与房价也有微妙的关系。近几年我国居民的储蓄额快速增长，在过去的5年时间里，居民储蓄额更是实现了翻番。投资渠道过少、投资产品缺乏，商品房投资在价格的快速上涨中基本绑架了居民的投资行为、投资能力和投资方向。加上其他的投资产品风险极大，且收益状况根本弥补不了住房价格上涨带来的损失。第十，商品住宅均价。作为一种特殊商品，商品住宅也要遵循价值规律，即商品住宅价格的提高会减少消费者对房地产的需求；反之，商品住宅价格的下降会促使消费者对房地产商品需求量的上升。因此，商品住宅价格的高低对其需求量，特别是投资性需求有着重要的调节作用。但是房地产作为一种不动产，其价格和需求都有一定的特点，商品住宅价格对需求的影响较为复杂。

2.参数设定与数据预处理。第一，参数假设。设第i季度，固定资产投资为xi1，房地产开发投资为xi2，开工房屋施工面积为xi3，房屋竣工面积为xi4，商品房销售面积为xi5，国民生产总值为xi6，人均可支配收入为xi7，消费者物价指数（CPI）为xi8，居民储蓄额为xi9，商品住宅均价为xi10。第二，数据标准化。房地产行业涉及领域众多，影响商品住宅价格的诸多因素既有定性定量之分，又有量纲不同之别，这为后期数据的处理和运算带来了较大难度，因此，采用指数化处理方法，对各个指标相对应的数据进行预处理，以指标的最大值和最小值的差距进行数学计算，使其结果介于0～1 之间。第三，主成分分析。在面板数据中，共有10个指标，数量繁多、类型复杂，为了减少数据指标信息的重叠和无关信息的干扰，先对数据进行降维处理，选用主成分分析，即通过构造原变量的适当线性组合，产生出一系列互不相关的新变量，从中选出少数几个新变量并使它们含有尽可能多的原变量所包含的信息。然后，使用SPSS软件进行计算，在采用主成分分析法对各指标进行优化分析前，需对其进行巴特莱特球形检验，计算KMO值，通过综合考虑，判断是否应对该指标进行主成分分析。经统计计算，KMO 值为0.85，大于0.7，适合做主成分分析。通过计算发现，前两个主成分信息量大于80%，同时特征值大于1，体现了原始数据的主要信息。据此，提取前两个主成分，主成分矩阵见表1。由表1可知，第一主成分主要体现为固定资产投资、房地产开发投资、开工房屋施工面积、生产总值、人均可支配收入、居民储蓄额、商品住宅均价及商品房销售面积的信息；第二主成分主要体现为房屋竣工面积、消费者物价指数信息，同时信息重要程度是依据每个因素的贡献度而决定的，又保留了原始数据的主要信息，依据主成分分析理论将原始面板数据从10 维降低到2维。即从（xi1，xi2，xi3，xi4，xi5，xi6，xi7，xi8，xi9，xi10）变换到（Zi1，Zi2）。

表1 主成分矩阵

其中f（x）为通过对样本集的学习而构造的回归估计函数，y为x对应的目标值，ε＞0为与函数估计精度直接相关的设计参数，该ε不敏感损失函数形象地比喻为ε管道。学习的目的是构造f（x），使与目标值之间的距离小于ε，同时函数的VC 维最小，这样对于未知样本x，可最优地估计出对应的目标值。对于训练集为非线性情况，通过某一非线性函数Φ（·）将训练集数据x 映射到一个高维线性特征空间，在这个高维数的线性空间中构造回归估计函数，因此，在非线性情况下，估计函数f（x）为如下形式：

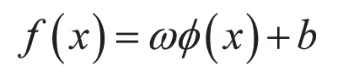
其中特征空间维数为ω的维数。

由统计学习理论知，结构风险最优化原则等价于下面的优化问题。

其中C＞0 为惩罚系数，C 越大表示对超出ε 管道数据点的惩罚越大。

本研究的中心问题是在本季度的以前的经济数据（包括本季度）已知的前提下，能否较为准确的预测下一个季度的商品住宅价格？我们知道商品住宅的价格形成跟经济数据有一定的关系，同时由于经济因素影响商品住宅价格也有一定的滞后性，本季度的一系列经济指标，会对下一个季度的商品住宅价格形成一定的影响，以此建立对应关系，即，其中1≤i≤35 由统计学知，直接估计对应关系f 是一件困难的事情［7］，在基于训练集已知的前提下，对第K季度的经济数据Zk1，Zk2，可以利用支持向量机预测出下一个季度的商品住宅价格。学习样本与预测样本的选择很重要，由于支持向量机对附近的点预测准确度比较高，如果预测时间过长，学习泛化性能就比较低，所以我们采用逐步预测的方法，即利用K 季度前的n 个季度相关数据进行学习，然后利用Zk1，Zk2，预测第K+1季度的商品住宅房价，逐步进行下去，经过实际测试，这种预测比整体预测效果好。

首先，利用2004 年、2005 年、2006 年共3 年12个季度的经济数据作为12 个学习样本，即Zi1，Zi2，1≤i≤12，它们的对应的输出值为下一季度的房价x（i+1）10，1≤i≤12。再以Z13,1，Z13,2作为预测样本，通过支持向量机预测出其值y14，以此类推。编程利用matlab 语言来进行计算，在计算中支持向量机的核函数及其参数的选择是一个十分重要的问题，我们将选取常见的高斯核函数，同时编程利用网格优化思想实现了支持向量机惩罚参数C和高斯核函数中σ的寻优，依据计算结果绘制了图1。

图1 郑州市商品住宅房价与预测房价图

4.预测结果分析。通过运用主成分分析对2002～2012 年房地产面板数据的分析表明，影响商品住宅价格的因素多种多样，它们之间的相互影响因素也相当复杂，通过主成分进行数据的降维，将众多信息归结为第一主成分与第二主成分，利用支持向量预测2006～2012年的商品住宅价格的平均相对误差为6.63%，比较准确地实现了本季度的经济数据对下一个季度商品住宅价格的预测，同时也可以看出商品住房房价预测具有一定误差及滞后性，预测房价落后的真实房价，同时政策因素和突发经济情况对预测的准确率影响较大，如在2008年经济危机的情况下及2010 年房地产调控政策频繁推出后，预测的误差就比较大。我们也看到商品住宅价格的形成在遵循商品价值规律的同时也有其特殊性，在刚性需求和投资需求主导的今天，买卖双方心理上的博弈，使商品住宅价格的预测变得更加困难。商品住宅的价格受政府房地产政策突变因素的影响是十分明显的，模型需要实际积累数据才能适应这样一变化，此外考虑加入政策因子，使模型更加稳定成熟。

［1］郭培俊，毛海舟.基于灰色理论的温州房价预测模型［J］.数学的实践与认识，2011，（20）.

［2］闫妍，许伟，佳慧.基于TEL@I方法论的房价预测方法［J］.系统工程与实践，2007，（7）.

［3］谈萍，史占中.基于灰色马尔可夫模型的上海房价走势实证研究［J］. 科学技术与工程，2011，（3）.

［4］程松林.武汉市商品房均价的预测［J］.统计与决策，2008，（2）.

［5］Vapnik V. An Overview of Statistical Learning Theory［J］.IEEE Transactions on Neural Networks，1999，（5）.

［6］Vapnik V. The Nature of Statistical Learning Theory［M］.New York：Spring-Verlag，1995.

［7］张彦周.基于支持向量机的测井曲线预测储层参数方法［D］.西安：西安科技大学，2006.