非均匀线阵的快速求根MUSIC方法∗
陈柱学,吴建新
(1.中国电子科技集团公司第三十八研究所,安徽合肥230088;2.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)
0 引言
DOA估计是阵列信号处理的一个重要应用[1-3]。在各种DOA估计方法中,MUSIC方法[4-5]由于它的性能优异而得到了广泛应用。但传统MUSIC方法需要进行角度搜索,精细的角度搜索往往导致很大的计算量。为了减少搜索运算,Bhaskar提出了求根 MUSIC方法[6],它将DOA估计转化为复多项式求根问题,直接由复根的相位来确定角度。但求根MUSIC方法要求阵列为均匀阵列,对于非均匀阵列,该方法就会失效。在阵元数相同的情况下,非均匀线阵能够达到比均匀线阵更大的孔径,提高了角分辨率[7]。因此,非均匀阵列的DOA估计是实际应用中面临的一个重要问题。Friedlander和Doran针对非均匀阵列分别提出了阵列内插方法[8]和流型分离方法[9],将非均匀阵列变换成虚拟均匀阵列。于是各种适合于均匀阵列的各种DOA算法,包括ESPRIT方法[10]和求根MUSIC方法都能应用于非均匀阵列。但是阵列内插方法和流型分离方法要求虚拟均匀阵列孔径大小不小于非均匀阵列孔径大小的两倍,否则精度会变差。因此,虚拟均匀阵列一般都比较大,直接采用求根MUSIC方法需要对高阶多项式进行求根运算,计算量很大并且数值不稳定。
针对非均匀线阵DOA估计带来的高计算量问题,本文提出了一种快速的多项式求根MUSIC方法。该方法利用小角度范围内的导向矢量可以利用低阶多项式很好近似的特性,将非均匀线阵DOA估计问题转化为多组低阶实多项式求根问题。由于低阶实多项式具有计算量小以及数值稳定性好等优点,而且多组多项式求根可以并行实现,该方法能够快速地实现非均匀线阵DOA估计,非常适合于工程应用。
1 信号模型
考虑N个阵元的线阵,其第n个阵元相对于第1个阵元的间距为d n,其中d1=0,其阵列示意图如图1所示。假设有P个远场基带信号入射到该阵列,其中第p个信号s p(k)的入射方向与阵列法线方向夹角为θp。k时刻第n个阵元的接收回波信号x n(k)可以表示为

式中,λ表示波长;w n(k)表示k时刻第n个阵元的高斯白噪声。将式(1)写成矢量形式为



图1 非均匀阵列示意图
回波数据对应的协方差矩阵可以表示为
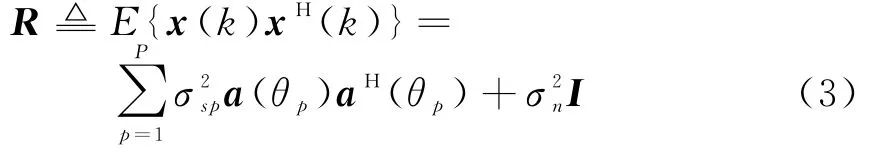
一般情况下理想的协方差矩阵是得不到的,需要从数据中估计得到,一般采用如下方式估计:对估计的协方差矩阵进行特征分解,
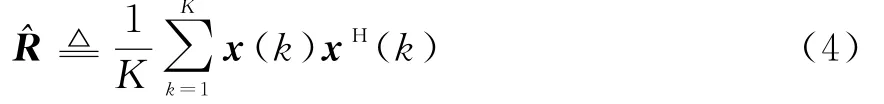

传统的M USIC算法[1]构造如下的代价函数:
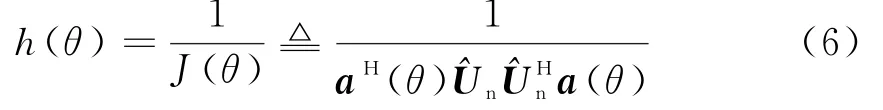
对于非均匀阵列来说,我们可以通过各种途径将其变换成均匀阵列。两种常用的变换方法是阵列插值方法[4]和阵列流型分离方法[5]。这两种方法可以统一写为

将式(7)代入到MUSIC倒数谱可以得到

由于aT(θ)是一个等比数列,我们可以直接利用求根MUSIC方法将上述代价函数转化为复多项式,也就是令并且
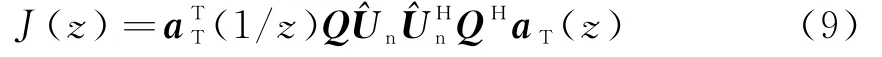
上式是关于z的2Q-2阶复多项式,对这么高阶的复多项式进行求复根运算所需要的计算量很大,并且数值稳定性也不好,很不利于工程实现。比如对于一个长度为10λ的6个阵元的非均匀线阵,其虚拟均匀线阵的半波长阵元数为40,此时式(9)的多项式阶数为78阶。为了降低非均匀阵列求根MUSIC方法的计算量,需要采用有效的近似方法。
2 快速实多项式求根MUSIC方法



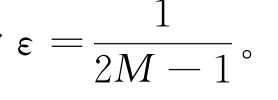

式中,g∈[0,ε]。对应地,落在第k个区间内的频率对应的导向矢量可以表示为

式中,u k=[e-j2π(M-1)εk… 1 … ej2π(M-1)εk]T,c k(g)表示第k个区间的导向矢量。将式(14)代入到式(10)可以得到第k个区间内的M USIC倒数谱为

式中,7表示Hadamard积;Φ=diag(b)表示对角元素为b的对角矩阵。
对于落在小区间内的导向矢量来说,由于它具有低秩特性,可以采用低阶多项式来近似。低阶多项式近似需要求解如下的最优化问题:
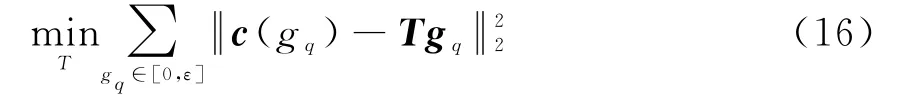
式中,‖·‖2表示2范数;为L阶多项式矢量;T=[t1t2…t L+1]∈C M×(L+1)为多项式拟合矩阵。在式(16)中,多项式阶数L影响着近似的精度,L越大,近似精度越高,但后续的多项式求根的计算量也就越大。图2给出了不同阶数情况下的拟合误差情况。从图中可以看出,当L大于等于5的情况下,各个频率的近似误差可以在-40 dB以下,也就是近似的导向矢量与实际的导向矢量的相关系数可以达到0.999 9。因此,L等于5时就可以获得很高的近似精度。

图2 不同阶数情况下的拟合误差(M=16)
式(16)是一个经典的最小二乘问题,其最优解[13-14]为

式中,C=[c(g1)c(g2) …c(g I)],G=[g1g2…g I],I为区间内的频率网格点数。这样就可以得到低阶近似后的导向矢量为

将式(18)代入到式(15)可以得到用低阶多项式表示的MUSIC倒数谱
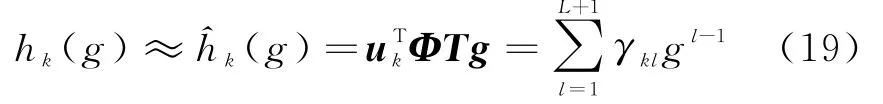
1.2.4 疼痛评分 采用11点数字评分法,以无痛为“0”,最剧烈疼痛为“10”,共11个点描述疼痛程度,分值越高,疼痛程度越重。患者根据自己的疼痛感觉在相应的分值处划对号。


式中 ,z=[z11…z1N z21…z NN]T,w kl=[w kl11…w kl1N w kl21…w klNN]T。根据式(21),第k个区间的多项式系数矢量可以写成
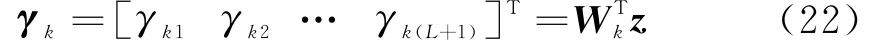
式中,W k=[w k1w k2…w k(L+1)]∈C N2×(L+1)。
最后,令低阶多项式式(19)等于零,也就是

式(23)的共轭复根的虚部大小可以作为是否是信源的判断标准,虚部值越接近于0,表示该共轭复根越有可能是信源对应的共轭复根,而实部就是估计的角度。
为了使这个算法更加清楚,我们给出了该算法的处理流程:
1)离线计算独立于数据的降维矩阵{W1,W2,…,W K};
2)根据噪声子空间计算矢量z;
3)对第k个角度区间,根据式(22)计算L+1个多项式系数γk1,γk2,…,γk(L+1);
4)对第k个角度区间的多项式式(23)进行多项式求根;
5)重复步骤3和4直到所有角度区间处理完毕,得到所有的共轭复根,然后根据复根的虚部大小判断信源对应的根,也就是挑选虚部值最小的P个根,根据根的实部直接计算信源的角度。
根据处理流程,本方法总的计算量为O(4N2P+2(L+1)N2+4ML2)实数乘法,而标准的求根M USIC方法的计算量为O(4N2P+32M3)。由于M远大于N和L,标准的求根M USIC方法的计算量要远大于本文方法的计算量。图3给出了本方法的流程图。
3 仿真实验
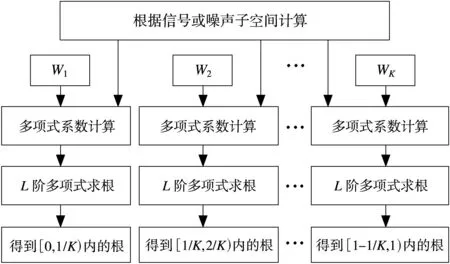
图3 本文方法的处理流程图
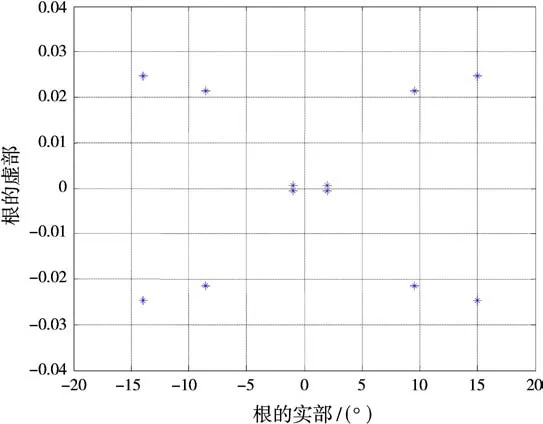
图4 本方法获得的MUSIC谱对应的共轭复根分布
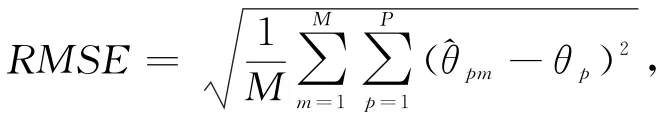

图5 均方根误差随信噪比的变化关系
图6给出了标准求根MUSIC方法与本方法的均方根误差随快拍数的变化关系,其中本方法采用的多项式阶数为5阶,信噪比为5dB。从图中可以看出,两种方法的均方根误差随着快拍数的增加而减小,而且对于不同的快拍数,本方法都可以获得与标准求根MUSIC方法基本相同的性能。另外,随着快拍数增加到一定程度,均方根误差性能的改善逐渐趋缓,这主要是由于求根MUSIC方法的收敛性能是非线性的,快拍数比较少时收敛性能改善快,快拍数比较多时基本收敛,此时的收敛性能改善慢。
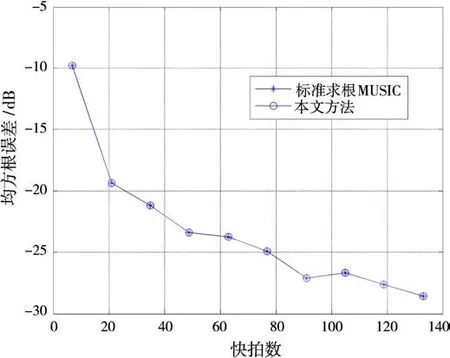
图6 均方根误差随快拍数的变化关系
4 结束语
针对非均匀线阵DOA估计带来的高计算量问题,本文提出了一种快速求根MUSIC方法。该方法利用小角度范围内的导向矢量可以利用低阶多项式很好近似的特性,将非均匀线阵DOA估计问题转化为多组低阶实多项式求根问题。该方法能够在性能基本保持不变的情况下大大降低标准求根MUSIC算法的计算复杂度,非常适合于工程应用。
[1]王永良,陈辉,彭应宁.空间谱估计理论与算法[M].北京:清华大学出版社,2004.
[2]刘周,李军,刘红明,等.MIMO雷达非严格正交信号单脉冲测角方法[J].雷达科学与技术,2013,11(3):262-266.LIU Zhou,LI Jun,LIU Hong-ming,et al.Monopulse Angle Measurement of Non-Strictly Orthogonal Signals for MIMO Radar[J].Radar Science and Technology,2013,11(3):262-266.(in Chinese)
[3]林文凤,周晓青,甘露,等.一种可自动配对的二维波达方向估计算法[J].雷达科学与技术,2013,11(1):33-39.LIN Wen-feng,ZHOU Xiao-qing,GAN Lu,et al.An Automatic Pairing Method for 2-D Direction of Arrival Estimation[J].Radar Science and Technology,2013,11(1):33-39.(in Chinese)
[4]Schmidt R O.Multiple Emitter Location and Signal Parameter Estimation[J].IEEE Trans on Antennas and Propagation,1986,34(3):276-280.
[5]黄秋钦,余嘉,梁炎夏,等.基于改进PASTd的MUSIC算法的DSP实现[J].雷达科学与技术,2010,8(2):183-187.HUANG Qiu-qin,YU Jia,LIANG Yan-xia,et al.The Implementation of Modified PASTd Algorithm Based on DSP System[J].Radar Science and Technology,2010,8(2):183-187.(in Chinese)
[6]RAO B D,HARI K V S.Performance Analysis of Root-Music[J].IEEE Trans on Acoustics,Speech and Signal Processing,1989,37(12):1939-1949.
[7]KASSIS C E,PICHERAL J,MOKBEL C.Advantages of Nonuniform Arrays Using Root-MUSIC[J].Signal Processing,2010,90(2):689-695.
[8]FRIEDLANDER B.The Root-MUSIC Algorithm for Direction Finding with Interpolated Arrays[J].Signal Processing,1993,30(1):15-29.
[9]DORAN M A,DORON M A,WEISS A J.Coherent Wide-Band Processing for Arbitrary Array Geometry[J].IEEE Trans on Signal Processing,1993,41(1):414-417.
[10]GERSHMAN A B,RUBSAMEN M,PESAVENTO M.One-and Two-Dimensional Direction-of-Arrival Estimation:An Overview of Search-Free Techniques[J].Signal Processing,2010,90(5):1338-1349.
[11]WU J X,WANG T,BAO Z.Angle Estimation for Adaptive Linear Array Using PCA-GS-ML Estimator[J].IEEE Trans on Aerospace and Electronic Systems,2013,49(1):670-677.
[12]WU J X,WANG T,BAO Z.Fast Realization of Maximum Likelihood angle Estimation with Small Adaptive Uniform Linear Array[J].IEEE Trans on Antennas and Propagation,2010,58(12):3951-3960.
[13]康兆敏.数值计算方法[M].北京:清华大学出版社,2013.
[14]苏峰,王昌海,徐征.基于最小二乘的时差定位算法[J].雷达科学与技术,2013,11(6):621-625.SU Feng,WANG Chang-hai,XU Zheng.TDOA Location Algorithms Based on the Least Squares[J].Radar Science and Technology,2013,11(6):621-625.(in Chinese)

