基于特征空间的极化敏感阵列滤波分析∗
刘 芳,李会勇
(电子科技大学电子工程学院,四川成都611731)
0 引言
极化敏感阵列可以获取空间电磁信号的极化信息,因而具有比传统标量阵列更优越的系统性能[1],而现有的对极化敏感阵列的研究大多在信号参数估计方面,对其在滤波方面的应用及其性能的讨论甚少。文献[2]分析了完全极化情形下极化敏感阵列的滤波性能;文献[3]讨论了单个电磁矢量传感器的波束形成问题;文献[4]分析了参数估计误差对极化滤波性能的影响;文献[5]提出了基于特征空间的广义波束形成算法;文献[6]在文献[5]的基础上分析了一种极化域-空域联合的自适应波束形成算法。为了充分利用极化敏感阵列滤波的性能优势,本文将特征空间的方法和多线性约束最小方差波束形成准则联合应用到极化敏感阵列滤波中,给出了一种极化域-空域联合滤波的方法,分析了其性能,并通过计算机仿真验证了理论的正确性。
1 系统模型
极化敏感阵列由M个相互正交的电偶极子对构成,阵列结构如图1所示。两个正交的电偶极子分别沿x轴和y轴方向放置,各个阵元沿y轴排列构成均匀线阵,阵元间距为d。
假设空间有1个期望信号和J个干扰信号入射到阵列,信号之间互不相关,阵列接收信号模型X(t)可以表示为
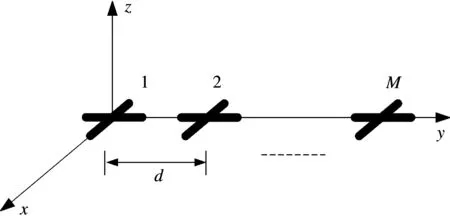
图1 极化敏感阵列结构图
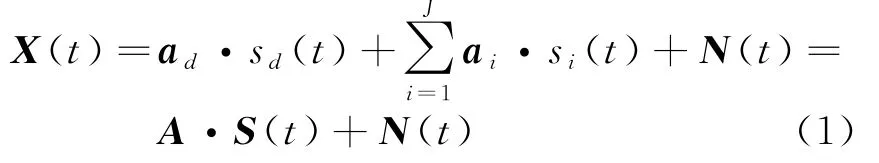
式中,s d(t),s i(t)分别为期望信号和干扰信号;N(t)为零均值的复高斯白噪声;a d,a i分别为期望信号和干扰信号的极化域-空域联合导向矢量,它是极化导向矢量和空间导向矢量的Kronecker乘积,即

式中,
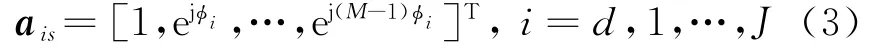
a is是信号的空间导向矢量的表达式,其中ϕi=2πdsinθi/λ,i=d,1,…,J。
对于分别沿x轴和y轴方向放置的两个正交的电偶极子,其极化导向矢量[1]可以表示为
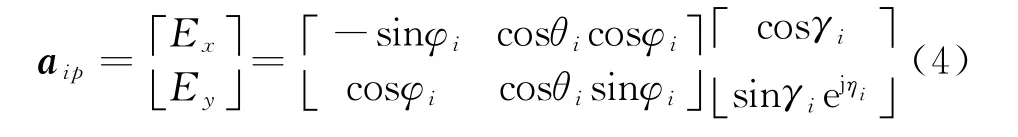
式中,γi和ηi分别为极化相角和极化相位差。
阵列输入信号的自相关矩阵:

式中,R S为输入信号S(t)的自相关矩阵;σ2n为高斯白噪声的功率。对自相关矩阵进行特征分解可得

可以证明span{μ1,μ2,…,μ1+J}=span{a d,a1,…,a J}并称其为信号子空间E S,噪声子空间EN=span{μJ+2,…,μ2M}。
阵列输出信号可表示为

2 基于特征空间的极化敏感阵列滤波方法
将线性约束最小方差波束形成器(LCMVB,Linearly Constrained Minimum Variance Beamformer)应用到极化阵列滤波中,称为极化域-空域联合多线性约束最小方差波束形成器(SPLCMVB),它可以包含多个约束条件,即
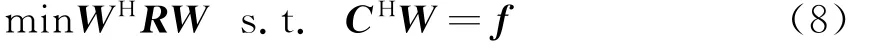
式中,C∈C2M×P和f∈C P×1分别为约束矩阵和对应的约束响应向量,常见的约束有导数约束和零点约束。SPLCMVB的最优权向量为
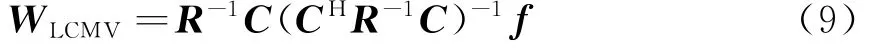
基于特征空间的极化敏感阵列滤波的基本思想是将SPLCMVB的最优权向量向一个子空间投影。投影矩阵在保证对期望信号和干扰信号响应不变的情况下,使得最优权向量的模减小,以至于输出噪声功率降低。通过正确的构建投影矩阵,可以灵活地选择保存或是不保存约束,下面将分别讨论这两种情形。
2.1 导数约束的情况
当阵列存在指向误差或是干扰或天线平台快速运动时,我们可以对阵列施加高阶导数约束,用来减少由指向误差引起的性能下降[7-8]。
假设除了期望信号方向的单位增益约束,还有导数约束CHuW=fu,首先计算SPLCMVB的最优权向量:
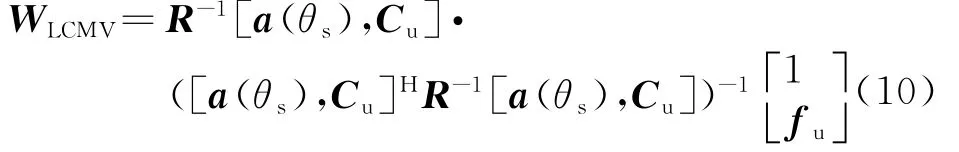
当存在指向误差时a(θs)一般与a(θd)不相等。
不保存约束的极化敏感阵列滤波方法将WLCMV投影到一个子空间,即

PSP-U是投影矩阵,因为导数约束不保存,选择PSP-U使‖WSP-U‖2最小,同时满足即对期望信号和干扰的响应不变,且使输出噪声功率最小。将WLCMV分解为正交的信号子空间最优权分量和噪声子空间最优权分量:
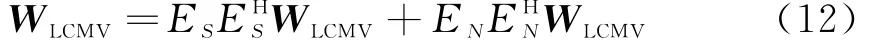
因为a i一定在由E S的列张成的信号子空间内所以a i在其空间的投影还是a i本身,即
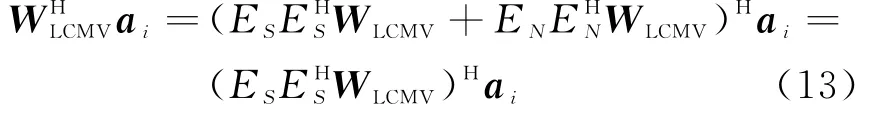
最优权向量在噪声子空间的投影对期望信号和干扰的响应没有任何影响,但是它增加了WLCMV的模,使输出信号的噪声功率变大。选择得到

2.2 零点约束的情况
当极化敏感阵列滤波后希望旁瓣某些位置零点依然存在,就需要保存零点约束的极化敏感阵列滤波方法。
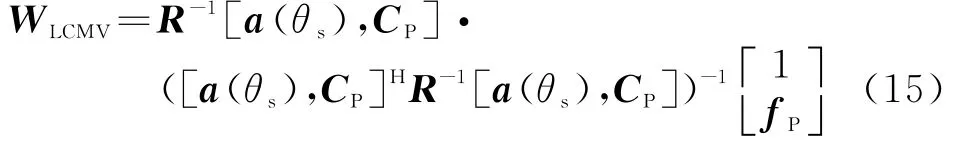
保存约束的极化敏感阵列滤波将WLCMV投影到一个子空间,即

PSP-P是投影矩阵,并且满足

可以看出,投影矩阵应该是由a i(i=d,1,2,…,J)和CP的列向量张成的子空间构成,定义其张成的子空间为修正的信号子空间。对特征向量μ1,μ2,…,μ1+J和约束矩阵CP的列进行施密特正交化,得到修正的信号子空间的正交基:
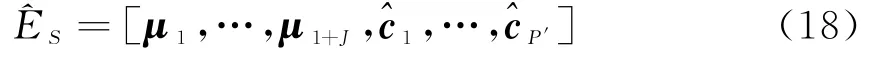
,i=1,2,…,P′在噪声子空间内。如果CP的某些列在信号子空间内,则P′将小于P。利用修正的信号子空间可以得到

WSP-P满足,即投影之后的权向量仍然满足零点约束条件。
2.3 滤波性能分析
假设入射信号都满足零均值平稳的特性,有
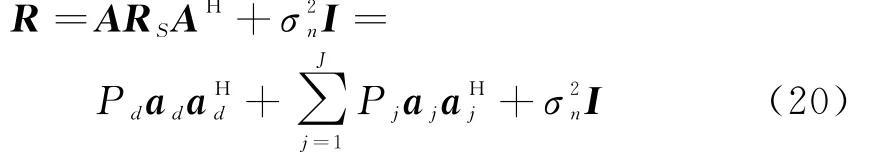
式中,P d为期望信号的功率,P j为第j个入射干扰信号的功率为噪声功率。设干扰和噪声的自相关矩阵为R i,即
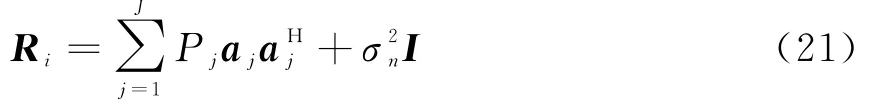
输出信号的功率为
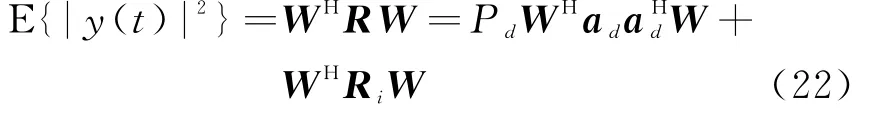
输出信干噪比(SINR)为
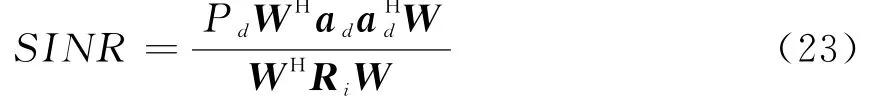
通过前面的分析可得:
(1)SPLCMVB输出SINR
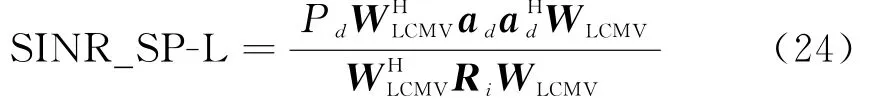
(2)导数约束的极化阵列输出SINR
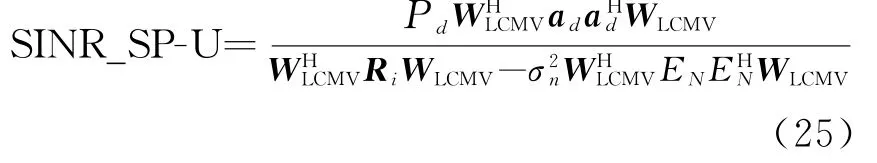
(3)零点约束的极化阵列输出SINR
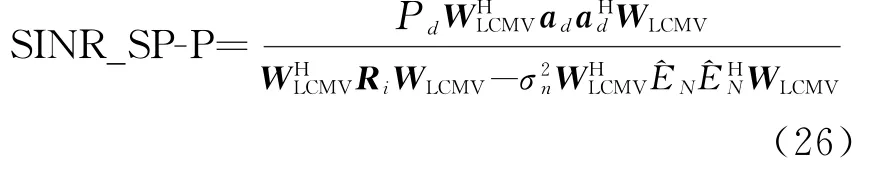
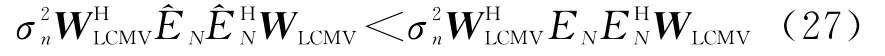
由此可见,三种情况下的输出信干噪比:

3 仿真分析
3.1 基于特征空间的极化滤波性能对比
仿真条件:采用8阵元均匀线阵,阵元间距为d=λ/2。本文中假设所有信号入射方位角φ=90°,期望信号俯仰角θ=0°,极化参量(γ,η)=(0°,90°),信噪比SNR=10 d B,两个干扰信号参量分别为θ1=20°,γ1=30°,η1=60°,INR1=25 dB;θ2=55°,γ2=10°,η2=35°,INR2=30 dB。图2给出了在导数约束下不同的指向误差与输出信干噪比SINR的变化情况。
从图2可以看出,与普通的SPLCMVB相比,存在导数约束的情况下基于特征空间的极化阵列滤波受指向误差的影响要小,这是因为投影操作降低了输出SINR对指向误差的敏感程度。
3.2 极化敏感阵列与标量阵列性能对比
图3给出了极化敏感阵列和传统的标量阵列滤波性能对比,仿真条件与3.1节相同。
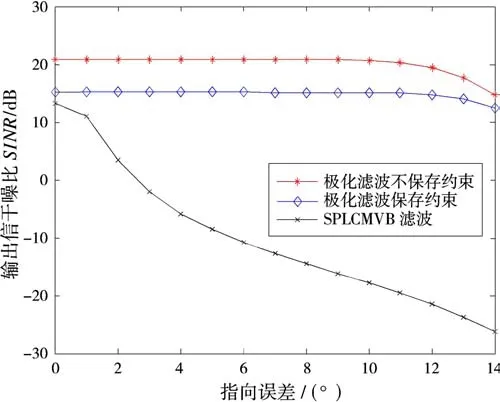
图2 极化滤波性能比较
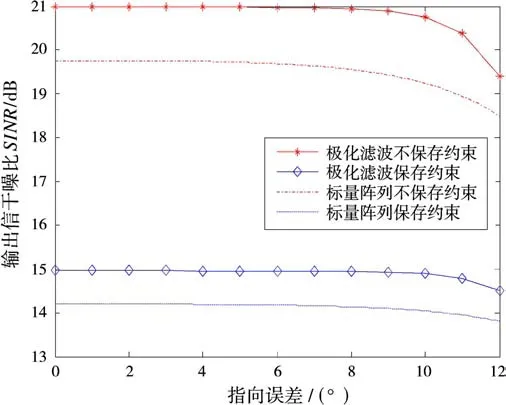
图3 极化敏感阵列和标量阵列性能对比
从图3可以看出,在相同的仿真条件下极化敏感阵列的输出SINR比标量阵列更高,这是因为极化敏感阵列能够更完整地接收电磁信号,这也是其相对于标量阵列的优势之一。
3.3 极化敏感阵列对不同约束性能对比
仿真参数设置同3.1节。图4给出了存在导数约束和两个零点约束条件下,输出SINR随指向误差的变化情况,约束的两个零点位置分别为θ01=25°,θ02=26°。
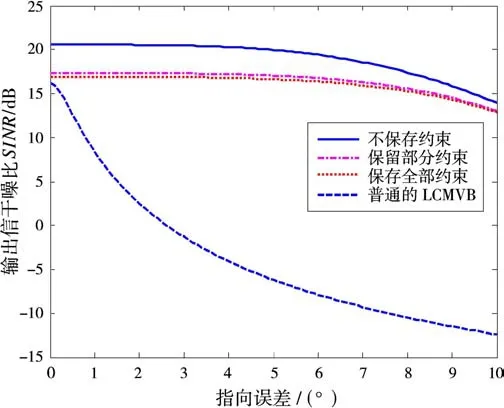
图4 不同的约束下输出性能对比
从图4可以看出,通过选择保存或是不保存约束,其输出SINR与理论分析的一致,完全不保存约束的情况下输出SINR最高,全部保存的情况下SINR最低,保存约束的代价就是增加了输出噪声功率,降低了输出SINR。
4 结束语
本文将基于特征空间的多线性约束最小方差波束形成器应用到极化敏感阵列滤波中,并在有导数约束和零点约束的条件下通过灵活的选择是否保存约束以满足特定的需求,理论分析表明基于特征空间的极化敏感阵列滤波具有比普通SPLCMVB更好的滤波性能,计算机仿真结果也验证了理论的正确性。
[1]庄钊文.极化敏感阵列信号处理[M].北京:国防工业出版社,2006:30-80.
[2]徐振海,王雪松,肖顺平,等.极化敏感阵列滤波性能分析:完全极化情形[J].电子学报,2004,32(8):1310-1313.
[3]NEHAORAI A,HO K C,TAN B T G.Minimum-Noise Variance Beamformer with an Electromagnetic Vector Sensor[J].IEEE Trans on Signal Processing,1999,47(3):601-618.
[4]章力强,陈信,李相平,等.参数估计误差对极化滤波性能影响分析[J].雷达科学与技术,2012,10(2):198-202.ZHANG Li-qiang,CHEN Xin,LI Xiang-ping,et al.Impact of Parameter Estimate Error on Polarization Filtering Performance[J].Radar Science and Technology,2012,10(2):198-202.(in Chinese)
[5]YU J L,YEH C C.Generalized Eigenspace-Based Beamformers[J].IEEE Trans on Signal Processing,1995,43(11):2453-2461.
[6]郭玉华,常青美,余道杰,等.一种改进的极化域 空域联合的自适应波束形成算法[J].电子学报,2012,40(6):1279-1283.
[7]CHENG Nai-ping,NI Shu-yan,NI Zheng-zhong.A Direction Constrained Eigenspace-Based Beamforming Algorithm[C]∥2010 Second International Conference on Networks Security Wireless Communications and Trusted Computing(NSWCTC), Wuhan,China:[s.n.],2010:310-313.
[8]WU Si-jun,ZHANG Jin-zhong,ZHANG Shu.Robust Adaptive Beamforming Against Pointing Error[J].Journal of Harbin Engineering University,2005,26(4):531-535.
[9]李永祯,肖顺平,王雪松,等.雷达极化抗干扰技术[M].北京:国防工业出版社,2010:1-40.

