一种耦合检测和JPDA滤波的多目标跟踪算法∗

王云奇,孔令讲,易 伟,杨晓波

(电子科技大学电子工程学院，四川成都611731)

0 引言

现役雷达对目标的跟踪一般采用先检测后跟踪(DBT)体制，即先进行单帧门限检测判决得到点迹数据，然后对这些过门限的点迹数据进行凝聚、关联、滤波等处理，最终形成目标航迹[1-4]。在信噪比较高的情况下，传统DBT技术可以有效地实现对目标的检测和跟踪，且具有运算量小，雷达资源需求少等优点。然而随着现代隐身技术的不断发展，目标雷达截面积大幅减小，加之强杂波环境(城市、森林、山地等)的干扰，使得目标信噪比往往很低，这时DBT体制的检测和跟踪性能将会急剧恶化。

传统DBT体制中，检测与跟踪被视为两个独立的过程，并依据相互独立的准则优化各自的性能;然而作为系统的两个组成部分，检测与跟踪存在着必然的内在联系，传统DBT体制对两者所作的割裂处理，势必造成了整个检测跟踪系统的性能损失，因此联合优化检测与跟踪的性能成为当前的研究热点，国内外学者对此作了大量研究工作:文献[5-8]通过修正黎卡蒂方程(MRE)的迭代，对跟踪器的性能进行了预测，指出跟踪性能可表示为检测门限的函数，使得自适应的确定最优检测门限成为可能;文献[9]沿用MRE方法，对基于知识辅助的跟踪器的性能进行预测，同样确定了最优的检测门限;文献[10]提出了一种耦合检测器与跟踪器的新体制，该体制引入了从概率数据关联滤波器(PDAF)到贝叶斯检测器的反馈，这样使得整个检测跟踪系统的数据流向是双向的，回波信息得到了更充分的利用，提高了检测和跟踪性能，文献中称之为PDAF-BD算法。

以上所有工作均基于单目标假设，但实际中多目标跟踪是不可回避的研究课题，本文对PDAF-BD算法进行改进，重点研究了多目标情形下检测与跟踪联合优化的问题。文中利用多个并行的贝叶斯检测器分别对各目标进行检测，将检测到的所有量测点迹输入到JPDA滤波器进行数据关联，并预测各目标下一时刻的位置分布信息，各贝叶斯检测器将该分布信息作为先验信息用于下一时刻的检测判决，本文将该算法简称为JPDAFBD算法。JPDAF-BD算法的检测门限是面向目标的，且与位置密切相关:即针对不同目标、不同待检测单元自适应的采用不同检测门限;其有益效果更在于可以有效减少跟踪过程中不同航迹之间的相互干扰。仿真表明相比传统DBT体制下的多目标跟踪算法:即单帧依据纽曼皮尔逊(NP)准则进行检测，继而利用JPDAF滤波器跟踪的算法(简记为JPDAF-NP)，本文提出的JPDAF-BD算法可以在更低信噪比下对目标进行有效的检测和跟踪，且跟踪精度得到显著提高。

1 PDAF-BD算法概要

假设有n个目标，任一目标t的运动方程和量测方程分别如下[11]:

式中，x t(k)，z t(k)分别为目标t在k时刻的状态向量和量测向量;F t为状态转移矩阵，H t为观测矩阵;v t，w t分别为过程噪声和量测噪声，两者皆为独立的零均值高斯白噪声，其方差分别为Q t，R t。

关于PDAF-BD算法的详细推导可以参看文献[10]。这里仅给出该算法的概要。假设场景中仅有一个目标，且为Swerling I模型，背景噪声为高斯白噪声，则可构造如下两个检测假设:

式中，假设H表示位置z i(k)处无目标，回波仅为噪声;假设K表示位置z i(k)处有目标，ρ为信噪比;a i(k)表示k时刻第i个待检测单元的回波能量。依据贝叶斯准则可得如下判决:

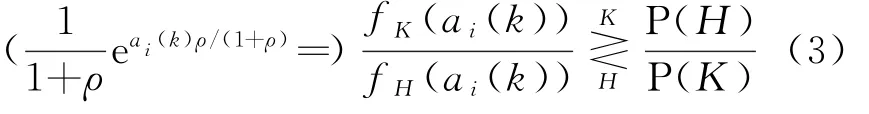
式中，P(j)表示假设j(∈ {H，K})的先验概率。依据PDAF滤波器的预测，P(K)∝P(H)∝ (1/V)，其中v i(k)表示z i(k)的新息，S(k)为新息自相关矩阵。于是检测过程可表示为

综合式(4)、式(5)最终可得检测判决如下:

对于通过检测门限的量测点迹，可以用标准的PDAF滤波器进行数据关联和跟踪预测，这里不再赘述，但其关联概率要作出修正[10]。

2 JPDAF-BD算法推导

PDAF-BD算法中检测门限在空间上是变化的，检测门限与待检测单元的位置，目标的预测位置以及新息自相关矩阵有关。图1是这种依赖待检测单元位置的检测器门限的示意图。

图1 与待检测单元位置相关的检测门限示意图

如图1所示，越靠近波门中心(目标的预测位置)，检测门限越低;反之门限越高。这样当对多个目标分别进行检测时，由于抬高了波门外围的门限，故而可以有效地减少邻近目标之间的干扰，即源自目标1的量测仅落入目标1波门，源自目标2的量测仅落入目标2波门。但此时量测点迹与各目标之间的关联概率需要重新计算，PDAF-BD算法已不再适用;本文提出的JPDAF-BD算法解决了上述问题，下文将给出量测点迹关联概率的详细推导及算法的实现流程框图。

对任一目标t，其k-1时刻的状态估计值为估计误差自相关矩阵为P t(k-1|k-1)，k时刻的m个量测值Z(k)=，截止到k时刻的所有量测值记为Z k={Z(k)，Z k-1}。

于是k-1时刻，目标t的状态预测值和位置预测值z t(k|k-1)分别为

k时刻，量测j对于目标t的新息及新息自相关矩阵可表示为

定义χjtj表示量测j源自目标表示联合事件，则联合事件的后验概率可表示为[12]

m

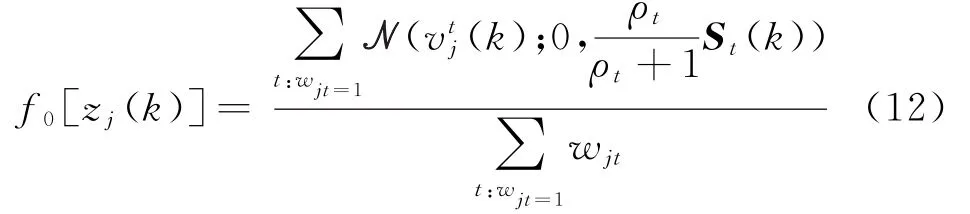
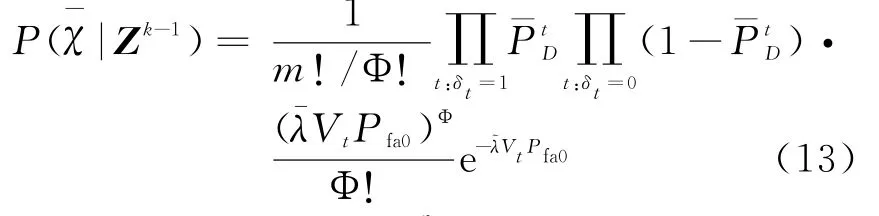
最终利用JPDAF滤波器，依据式(14)所给出的关联概率，可得k时刻目标t的状态估计值如下:

式中，W t(k)为滤波器增益;v t(k)为目标t的综合新息[10]。

综上所述，JPDAF-BD算法的实现流程框图如图2所示。

图2 JPDAF-BD算法实现流程图

其具体实施步骤如下:

步骤a 初始化各目标航迹，依据式(7)，(8)计算k时刻各目标的位置预测值及新息自相关矩阵S t(k)(t=1，2，…，n)。

步骤b 依据式(6)计算k时刻待检测距离单元i处各目标的检测门限，并完成检测判决。

步骤c 令i=i+1，重复步骤b，完成对k时刻整个数据平面中所有距离单元的检测。

步骤d 利用JPDA滤波器，并依据式(14)所给出的关联概率，对步骤b，c中所有检测到的量测点迹进行联合概率数据关联，得到k时刻各目标的状态估计值并预测k+1时刻各目标的位置，及k+1时刻的各目标的新息自相关矩阵S t(k+1)。

步骤e 令k=k+1，重复步骤b，c，d，得到所有时刻各目标的位置，最终输出各目标的航迹。

3 仿真及结果分析

图3、图4分别给出了一次典型实验中两种算法的检测跟踪结果。实验中两目标信噪比同为10 dB，两种算法虚警概率同为10-3。从图3中可见，对于JPDAF算法两条航迹之间的相互干扰现象严重，30帧中共检测到37个量测，其中29个量测(占总量测个数的78.4%)同时落入两个目标的波门之内;而对于JPDAF-BD算法，30帧中共检测到38个量测，只有13个量测(占总量测个数的34.2%)同时落入两个目标的波门内，可见JPDAF-BD算法有效地减少了两条航迹间的相互干扰。

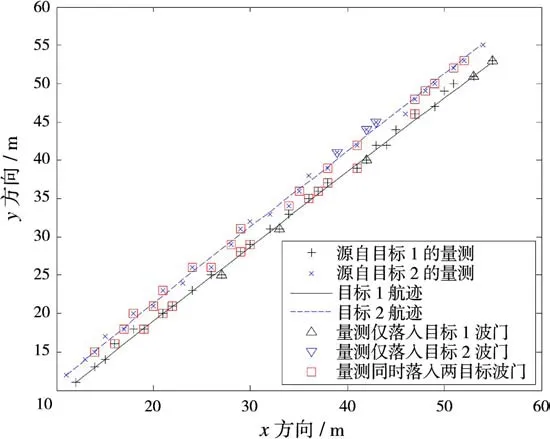
图3 JPDAF-NP算法检测跟踪效果图

图4 JPDAF-BD算法检测跟踪效果图

图5为两种算法检测概率曲线图。由于JPDAF-BD算法的检测门限是位置相关的，所以检测概率在空间上也是变化的，依据文献[10]的推导，其平均检测概率可表示为(其中ρ为信噪比，η为检测门限的调节参数)。图6给出了两种算法的成功跟踪概率曲线图。

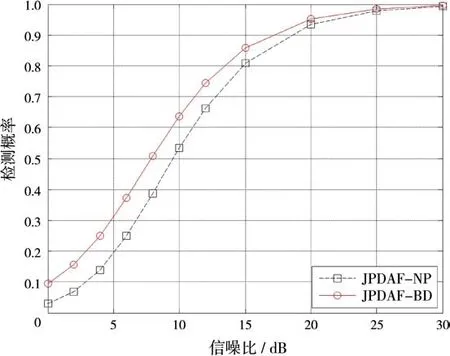
图5 不同信噪比下检测概率对比

图6 不同信噪比下成功跟踪概率对比

从图5和图6中可以看出，JPDAF-BD算法的检测概率、成功跟踪概率较之JPDAF-NP算法均有明显提高，在虚警概率=10-3，检测概率≥50%，成功跟踪概率≥50%的情况下，对输入信噪比的要求改善了约2 d B。图7给出了不同信噪比下两种算法的平均位置均方根误差[13]曲线图。在信噪比分别为4，6，8和10 d B情况下，位置均方根误差依次减少了12.5%，8.1%，4.9%和3.8%;可见JPDAF-BD算法的平均位置均方根误差在低信噪比下跟踪精度提高更加明显。由于本文主要研究的是航迹维持阶段，故而假设航迹已经起始，因此初始几帧的均方根误差较小，随着帧数增加逐渐稳定在一个固定的水平。如果考虑航迹起始时较大的不确定性误差，则会表现出一种随帧数变化均方根误差逐渐减小的特征。

图7 不同信噪比下两种算法的均方根误差曲线对比

传统JPDAF-NP算法中，随着目标个数、量测点迹个数以及波门相交程度的增大，可行联合事件的数量会迅速增大，要计算所有可行事件的联合概率可能会造成计算量爆炸。仿真中可见本文提出的JPDAF-BD算法，有效减少了由波门相交区域内量测所引起的不同航迹之间的相互干扰，因此会适度减少可行联合事件的数量，使得JPDAF-BD算法的时间复杂度略优于传统JPDAF-NP算法。考虑到工程实践中的应用，我们已着手研究一种次优的联合概率数据关联算法与贝叶斯检测相耦合，以获得更高效的计算效率。

4 结束语

本文提出了一种耦合贝叶斯检测和JPDA滤波的多目标跟踪算法，构造了多个并行的贝叶斯检测器，通过利用跟踪器的反馈信息，对不同距离单元、不同目标自适应地采用不同门限进行检测，从而有效提高了检测性能，并减少了不同航迹间的相互干扰，仿真结果表明，本文中所提出的JPDAF-BD算法与传统DBT体制下的JPDAFNP算法相比，在检测概率≥50%，成功跟踪概率≥50%的情况下，对输入信噪比的要求改善了约2 dB，且跟踪精度得到显著提高，因此能够实现更低信噪比下的多目标检测和跟踪。

[1]BAR-SHALOM Y，DAUM F，HUANG J.The Probabilistic Data Association Filter[J].IEEE Control Systems，2009，29(6):82-100.

[2]吴顺君.雷达信号处理和数据处理技术[M].北京:电子工业出版社，2008:533-538.

[3]KIRUBARAJAN T，BAR-SHALOM Y.Probabilistic Data Association Techniques for Target Tracking in Clutter[J].Proceedings of the IEEE，2004，92(3):536-557.

[4]HAO L.A Possibilistic Data Association Based Algorithm for Multi-Target Tracking[C]∥2013 Third International Conference on Intelligent System Design and Engineering Applications(ISDEA)，Hong Kong:IEEE，2013:158-162.

[5]FORTMANN T，BAR-SHALOM Y，SCHEFFE M，et al.Detection Thresholds for Tracking in Clutter-A Connection Between Estimation and Signal Processing[J].IEEE Trans on Automatic Control，1985，30(3):221-229.

[6]BOERS Y，DRIESSEN H.Modified Riccati Equation and Its Application to Target Tracking[C]∥IEE Proceedings-Radar，Sonar and Navigation，2006，153(1):7-12.

[7]ASLAN M S，SARANLI A.Threshold Optimization for Tracking a Nonmaneuvering Target[J].IEEE Trans on Aerospace and Electronic Systems，2011，47(4):2844-2859.

[8]ZENG T，ZHENG L，LI Y，et al.Offline Performance Prediction of PDAF with Bayesian Detection for Tracking in Clutter[J].IEEE Trans on Signal Processing，2013，61(3):770-781.

[9]BREKKE E，HALLINGSTAD O，GLATTETRE J.The Modified Riccati Equation for Amplitude-Aided Target Tracking in Heavy-Tailed Clutter[J].IEEE Trans on Aerospace and Electronic Systems，2011，47(4):2874-2886.

[10]WILLETT P，NIU R，BAR-SHALOM Y.Integration of Bayes Detection with Target Tracking[J].IEEE Trans on Signal Processing，2001，49(1):17-29.

[11]HABTEMARIAM B，THARMARASA R，THAYAPARAN T，et al.A Multiple-Detection Joint Probabilistic Data Association Filter[J].IEEE Journal of Selected Topics in Signal Processing，2013，7(3):461-471.

[12]FORTMANN T E，BAR-SHALOM Y，SCHEFFE M.Multi-Target Tracking Using Joint Probabilistic Data Association[C]∥1980 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes，[s.l.]:IEEE，1980:807-812.

[13]王峰，孔令讲，杨晓波.基于道路约束的粒子滤波检测前跟踪算法[J].雷达科学与技术，2011，9(6):525-530.WANG Feng，KONG Ling-jiang，YANG Xiao-bo.An Efficient Particle Filter Track-Before-Detect Algorithm with Road Constraints[J].Radar Science and Technology，2011，9(6):525-530.(in Chinese)