外辐射源雷达运动目标信号特性及检测方法研究∗

叶映宇,文铁牛,陈 俊,文童光

(成都中电锦江信息产业有限公司,四川成都610051)

0 引言

基于双基地连续波体制的短波外辐射源雷达系统以调幅广播信号为非合作照射源,可选辐射源多,选台灵活,具有频段反隐身、隐蔽性好、生存能力强等优点[1-2],成为雷达领域研究的热点方向。由于短波广播信号需传播上千公里,经目标反射后,目标回波信号强度很弱,对目标检测需要长时间积累以获得必要的信噪比,积累时间可达数十秒以上,目标长时间运动引起距离徙动和多普勒徙动。对于匀速运动目标,目标方位、仰角的改变引起多普勒频率的变化;对于机动目标,目标速度大小、方向的变化引起多普勒速度变化。脉冲体制雷达主要表现为跨距离徙动,而短波外辐射源雷达系统基于连续波体制,目标长时间运动引起多普勒频率徙动[3-4]。目前主要采取运动补偿等措施解决多普勒频率徙动的问题。这些措施主要包括分数阶傅里叶变换法、基于Wigner-Hough变换的检测方法和检测前跟踪等[5]。本文根据外辐射源雷达回波信号的特点,利用多项式拟合进行多普勒运动补偿,实现微弱回波信号检测,通过仿真分析和试验系统验证了该方法在长积累时间内对运动目标仍具有较好的检测性能。

1 运动目标回波模型

双基地短波外辐射源系统电波传播路径如图1所示。

图1 电波传播路径示意图

短波电台S发射单载频连续波,经电离层反射后到达目标T的发射传播路径为Rt1,由目标T散射后达到接收站R的接收传播路径为Rt2。设电台台标频率为fc,目标航速为V,目标航向与入射波方向夹角为θ1,目标航向与散射波方向夹角为θ2,则双基地目标回波信号可表示为

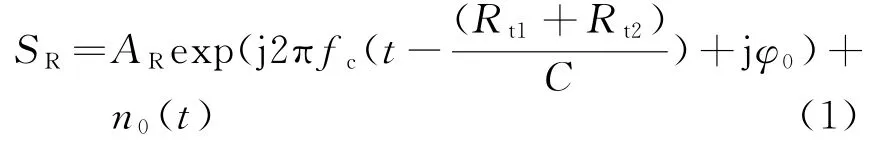
式中,AR为回波幅度,fc为载频,φ0为初相,n0(t)为高斯白噪声。根据瞬时频率定义有

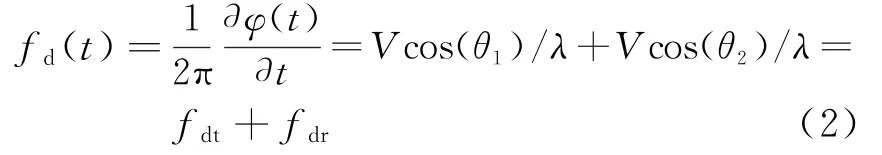
式中,φ(t)为目标回波相位。由于短波电台距离目标和接收站数千公里,接收站覆盖区域内电台来波方向可以认为处处相同,对于等高度匀速飞行目标发射多普勒fdt不变,所以双基地目标多普勒频率fd的变化近似为接收多普勒频率fdr的变化。

只考虑接收站多普勒变化时,令运动目标相对接收站运动的几何模型如图2所示。以接收站为坐标原点,建立直角坐标系(x,y),假设目标开始时位于(0,R0),速度为V,目标初始位置的运动方向与雷达视线的夹角为θ0。

任意时刻目标在直角坐标系(x,y)的坐标为

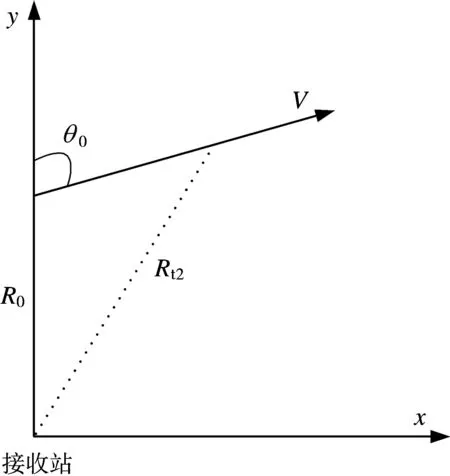
图2 目标运动几何模型

则目标相对接收站的瞬时距离为

利用马克劳林展开计算目标相对接收站运动引起的多普勒变化为

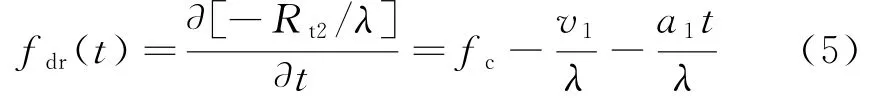
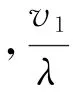
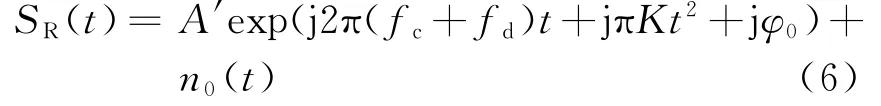
对于机动变速目标,由于目标高速及加速度的影响,目标径向速度仍然存在加速度[6],回波信号也可以视为线性调频信号。由于目标相对于雷达运动加速度的存在,相干积累时会出现多普勒谱展宽,在积累时间T内目标多普勒谱展宽为

2 基于运动补偿的检测算法

由上节讨论可知,非径向匀速直线运动目标回波模型可用线性调频信号表示,即使机动目标在短时间内也可用线性调频信号近似,若式中调频斜率K已知,则可利用多项式拟合方法进行多普勒补偿。通过对目标回波数据的运动补偿提高回波信噪比,进而提高外辐射源雷达对微弱目标检测的能力。检测算法框图如图3所示。

2.1 运动补偿原理

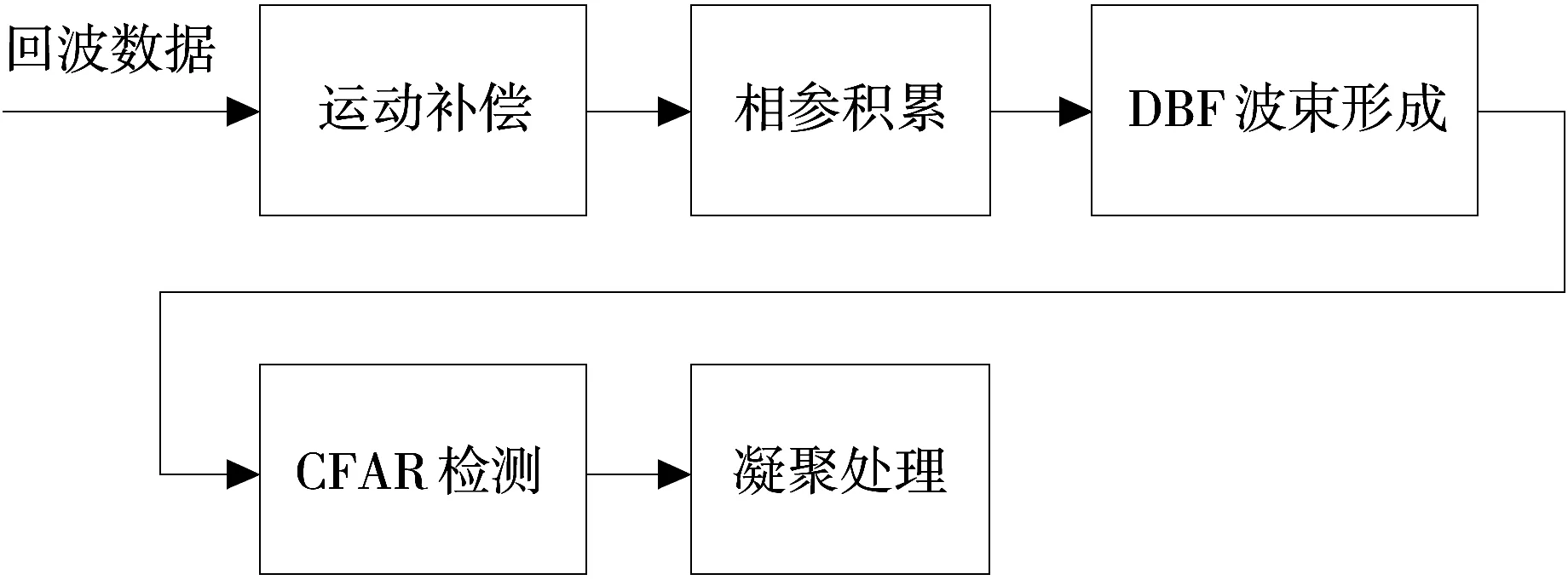
图3 检测算法框图

非径向目标回波信号形式如式(6)所示,则用exp(-jπKt2)对SR(t)进行补偿,得到：

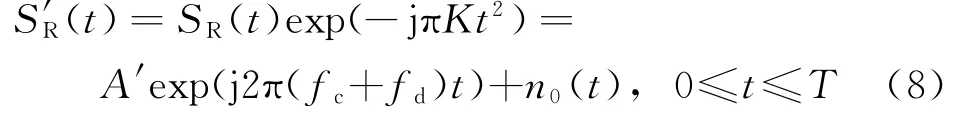
从式(8)中可以看出,运动补偿后,目标在积累时间内保持恒定的多普勒频率fd,则通过传统的相参积累方法傅里叶变换可完成目标的时域积累。

通常所探测目标为非合作目标,目标运动航向航速等信息均未知,也就是参数K为未知量,需要对调频斜率在一定范围内进行定步长搜索。为减小运算量,本文采用一阶多项式拟合补偿目标运动引起的多普勒频率变化,只需搜索一维参数(线性调频斜率),易于工程实现。

搜索步长的选择影响运动补偿效果。假设目标在积累时间T内多普勒频率变化为线性变化,则运动补偿的理论损失取决于多普勒频率变化斜率的搜索步长。图4(a)为运动补偿后目标频谱,每个频谱峰值对应不同搜索步长的积累效果;图4(b)为不同搜索步长下的失配损失。

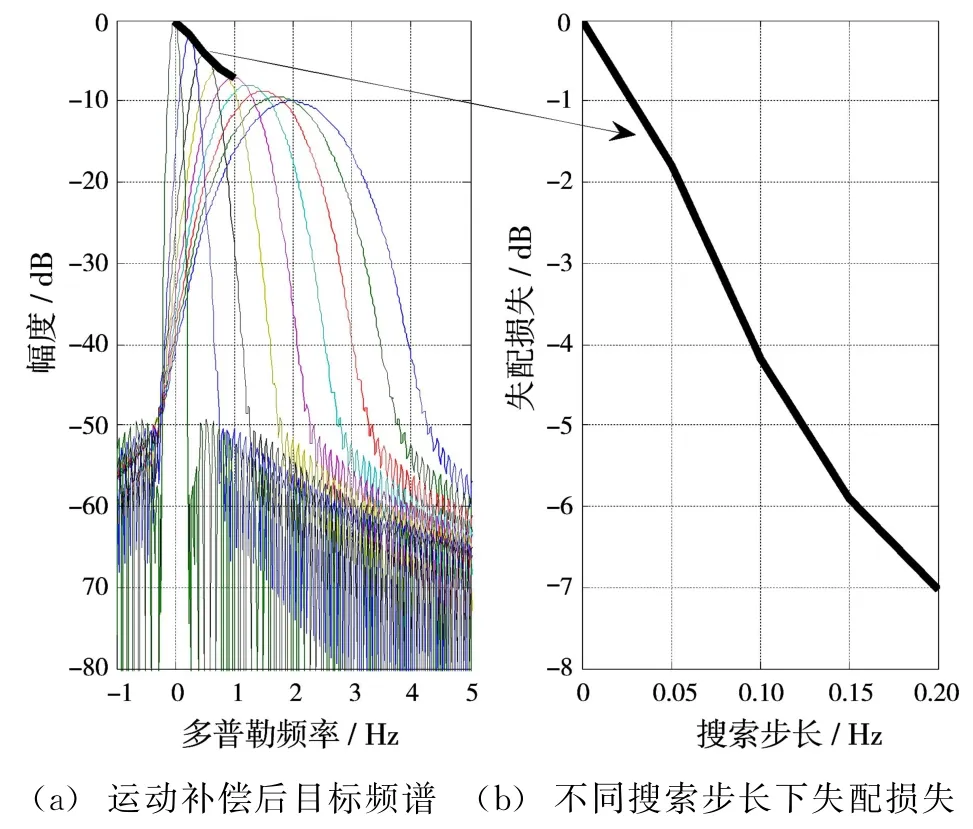
图4 K参数通道失配损失

当搜索步长偏移0.05时,失配损失为1.7 dB,搜索步长取0.1,失配损失约为4 dB。综合考虑系统所能承受的运算量和积累得益,运动补偿的多普勒频率变化率搜索步长取0.05。

2.2 补偿效果仿真分析

本节利用仿真数据进行基于运动补偿的检测算法性能验证,仿真参数如下：速度为3 Ma的切向运动目标,点频回波信号,时长为10 s,距离分别为50 km,采用一阶多项式拟合运动补偿方法进行运动补偿。目标多普勒展宽如图5所示,运动补偿后频谱变化如图6所示。

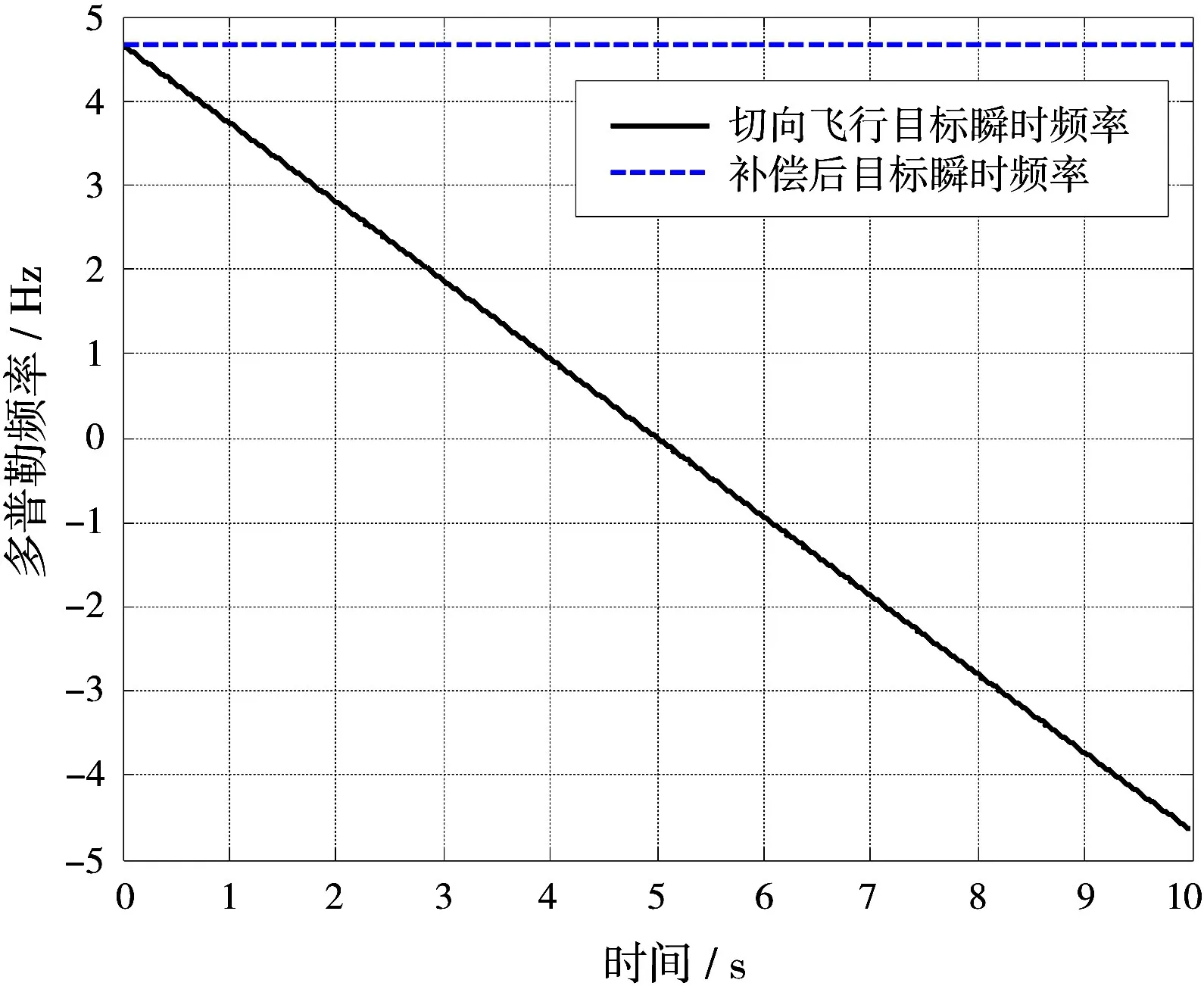
图5 50 km处切向目标的多普勒展宽

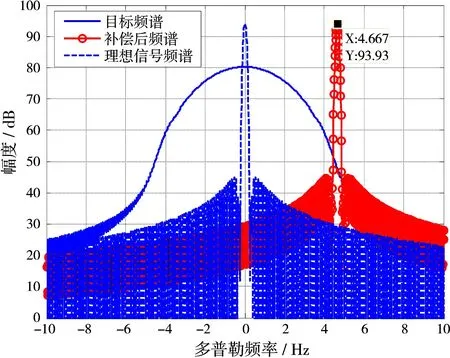
图6 补偿后回波频谱

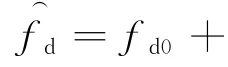
2.3 检测性能分析

对雷达回波数据进行上述检测算法处理,由于CFAR检测的虚警概率只与参考单元数及检测门限有关,运动补偿处理不改变噪声分布特性,理论上也不会改变检测算法的虚警率。为了验证该检测算法的性能,利用计算机仿真数据统计补偿前后该检测算法的虚警率和发现概率,如图7所示。

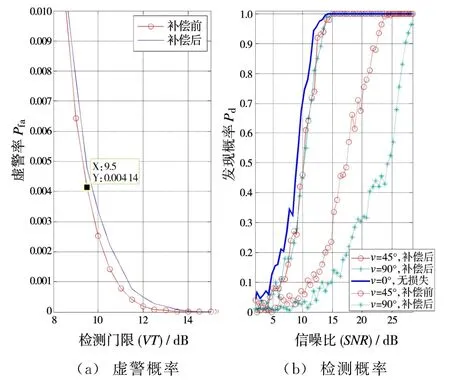
图7 补偿前后检测算法的检测概率(虚警率4×10-3)

从图7可以看出,基于多项式拟合的运动补偿积累算法不改变检测算法的虚警率,并且检测性能优于直接积累的检测性能。对于不同航向的目标均能有效积累增大信噪比,实现目标的有效检测。

2.4 实采数据验证

利用外辐射源试验系统实测数据进行积累性能验证,取目标多普勒频率变化最大的一段回波数据,多普勒变化如图8所示。图8为二次雷达测得的目标多普勒信息,二次雷达显示目标方位为-27°。

图9为该段实采8个通道的回波数据。

首先对采集的10 s数据进行运动补偿,为减少失配损失,K参数搜索步长取0.03,对补偿后的数据进行FFT积累,再形成-27°自适应波束。图10为运动补偿参数K搜索通道功率谱,从图中可以看出当K=-0.24 Hz时积累损失最小。

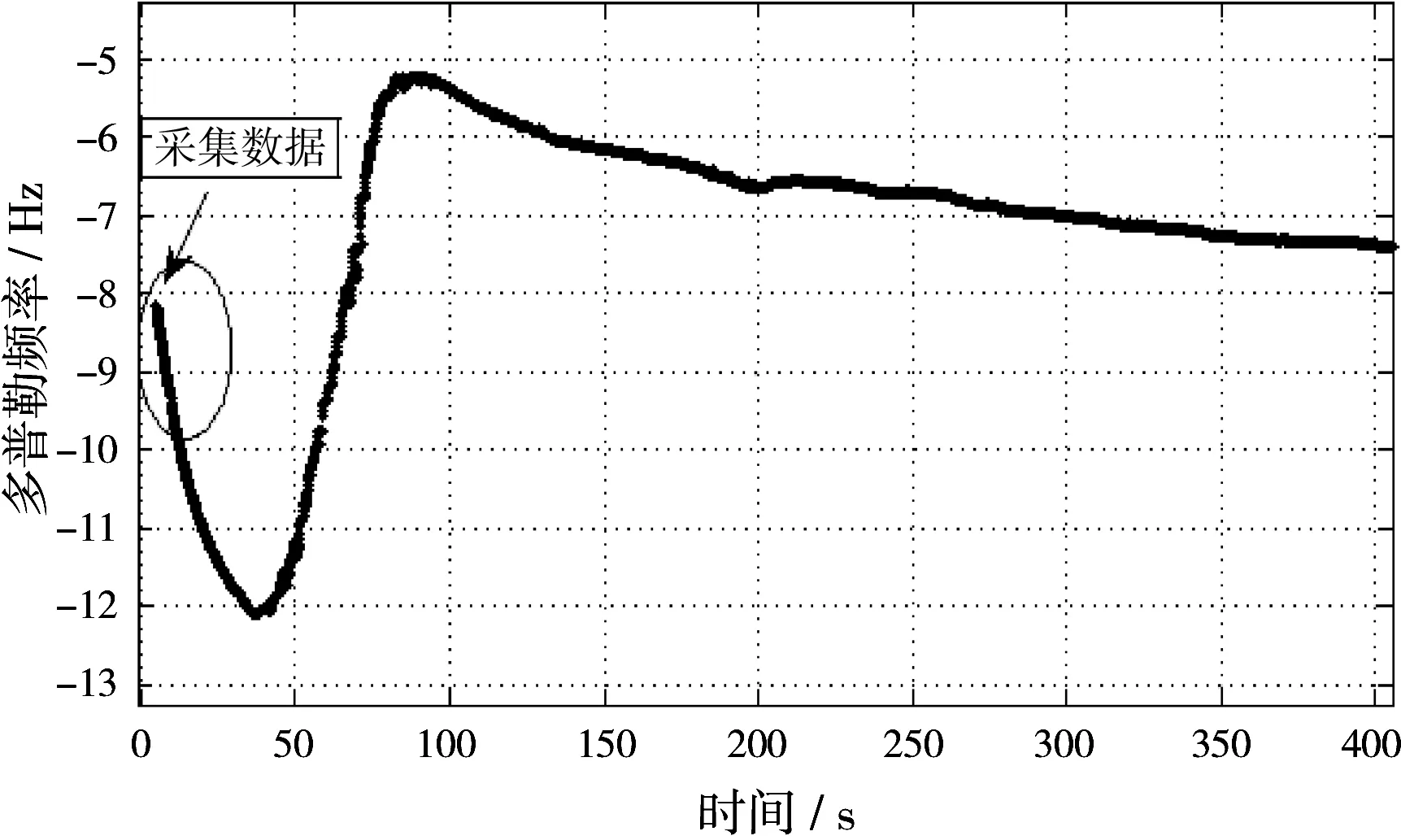
图8 二次雷达目标多普勒信息

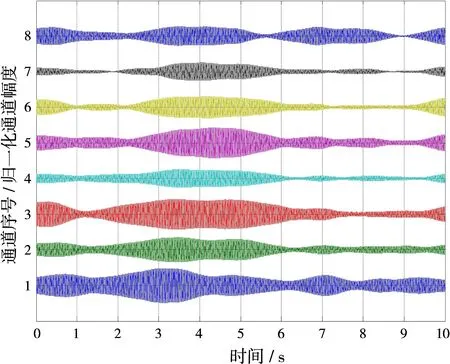
图9 回波数据

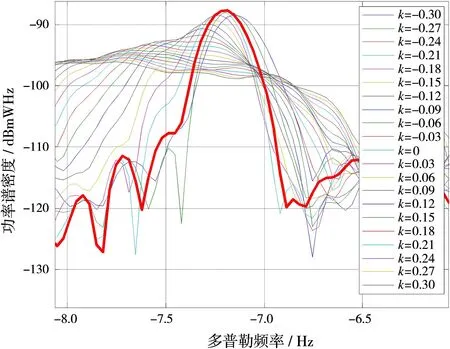
图10 运动补偿参数K搜索通道功率谱

图11为运动补偿前后目标信噪比得益的比较,从图中可以看出,通过运动补偿后,目标信杂噪比提高了9.8 dB。选取的数据段多普勒变化范围约为2 Hz,时长为10 s,考虑加窗引起的多普勒展宽,多普勒分辨单元约为0.133 Hz,则运动补偿信噪比理论得益约为11.8 dB。引起补偿损失的原因主要是：(1)由搜索步长量化产生的补偿失配损失;(2)电离层波动造成目标回波强度起伏产生的信噪比损失。

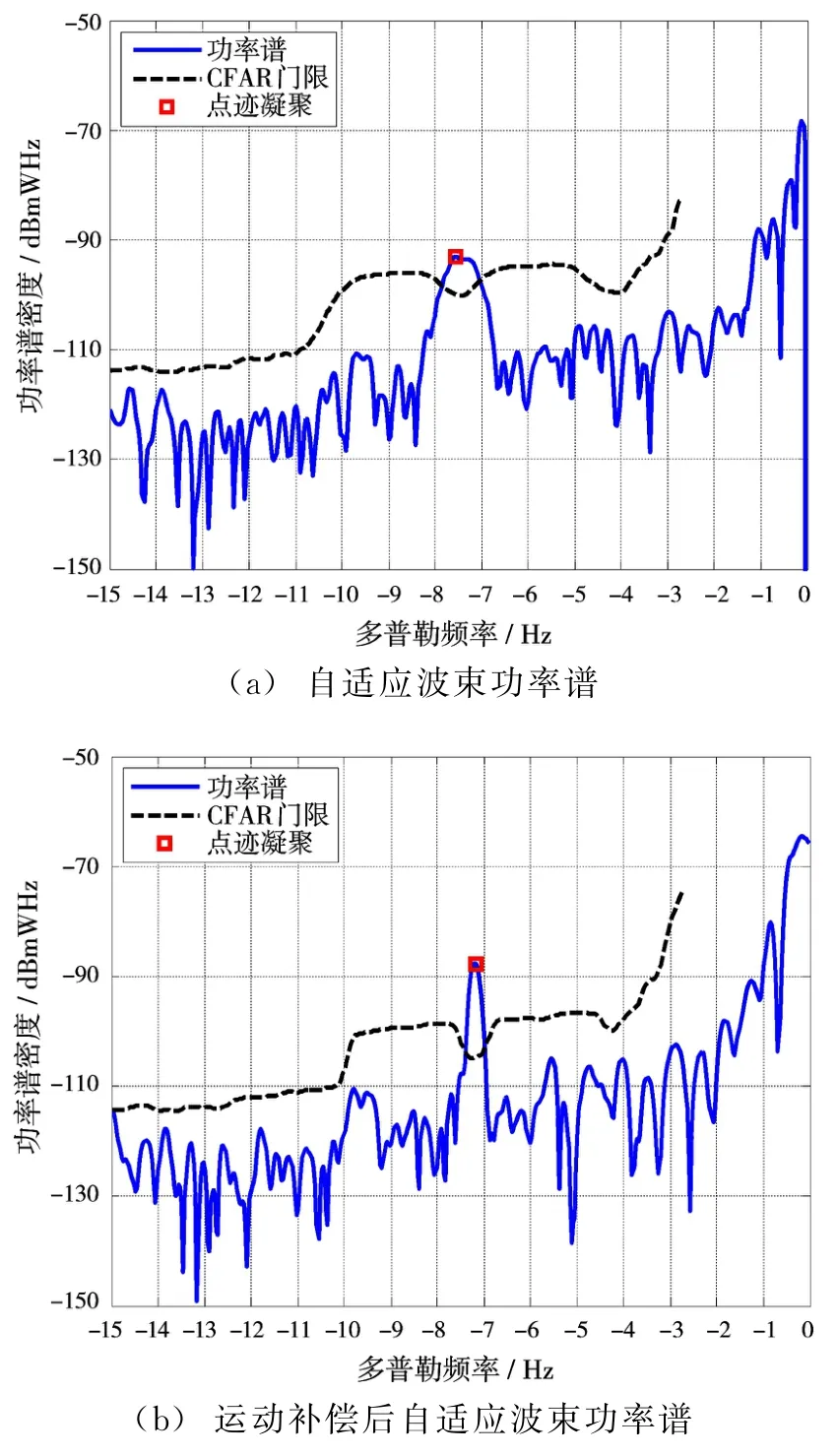
图11 运动补偿前后目标信噪比得益

综上所述,基于多项式拟合的运动补偿方法通过对由目标运动引起的相位进行补偿,再通过傅里叶变换实现微弱信号的长时间积累。利用仿真数据和试验数据进行算法性能验证,结果表明,经运动补偿后目标信噪比显著提高,实现了微弱信号长时间积累。

3 运算量分析

短波外辐射源信号处理框图如图12所示：从M根天线进入的信号分别进入M路接收机,经A/D采样后进行信号处理。首先分别对各个通道数据进行以长度为积累时间t的分段处理,对每一段数据作K维参数搜索的基于多项式拟合的运动补偿,形成参数通道 时间(K×M×t)三维数据结构;然后,对补偿后的数据在时间维作N点FFT相参积累;再进行空域自适应滤波形成波束通道,此时数据结构为参数波束频率(K×i×N)三维数据;对每个波束通道选大处理确定K参数后,对相应K通道数据进行CFAR检测;最后进行点迹凝聚处理。

双基地多普勒变化范围是目标距离、高度、航速、航向、电台方位和电台来波入射波仰角的函数。目标最大航速为3 Ma,高度为0,处理时段中心为轨迹切向点,电台方位为180°、电台来波入射波仰角为0°时是双基地多普勒频率变化的上限：

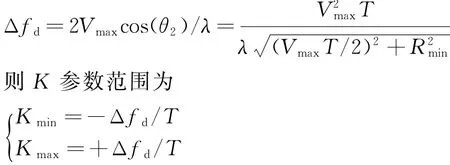
电台频率fc=13.5 MHz,信号最小作用距离为5 km,目标最大航速为3 Ma,取K参数维搜索步长为0.1 Hz,则K参数范围为[-6.5 Hz,6.5 Hz],K参数维通道数为130,即后续FFT、DBF和CFAR运算量增加130倍。

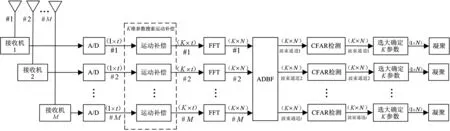
图12 短波外辐射源系统信号处理框图

4 结束语

在外辐射源雷达系统中,非合作照射源与非合作目标之间的运动导致回波信号很弱,传统的相参积累方法无法对长时间运动目标有效积累。针对这一问题,本文首先建立了目标回波模型,并在此基础上提出了基于多项式拟合的运动补偿方法,该方法基于参数搜索方法,经仿真和实测数据验证了该补偿算法的有效性,在目标多普勒频率变化较大时,该方法可以有效积累信号,提高信噪比。最后利用计算机建模仿真和真实目标数据验证该积累检测算法的检测性能,并进行了运算量评估。结果表明该方法实现简单,适合于工程应用。

[1]HOWLAND P.Passive Radar Systems[J].IEE Processing-Radar,Sonar and Navigation,2005,152(3)：105-106.

[2]PALMER J,PALUMBO S,SUMMERS A.An Overview of an Illuminator of Opportunity Passive Radar Research Project and Its Signal Processing Research Directions[J].Digital Signal Processing,2011,21(5)：593-599.

[3]关欣,胡东辉,仲利华,等.一种高效的外辐射源雷达高径向速度目标实时检测方法[J].电子与信息学报,2013,35(3)：581-588.

[4]葛先军,张财生,何友,等.无源雷达多站定位LFM弱信号检测[J].雷达科学与技术,2012,10(5)：529-532.

[5]杨金禄,单涛,陶然.外辐射源雷达高速加速微弱目标检测研究[J].现代雷达,2011,33(5)：30-35.

[6]苏洪涛,刘宏伟,保铮,等.天波超视距雷达机动目标检测方法[J].系统工程与电子技术,2004,26(3)：283-287.