基于学生“学”的教学思考
朱爱玲


一、问题的缘起
在学习完苏教版小学数学三年级下册“年、月、日”单元时,有这样一道题目:“小明从7月8日开始学习游泳,到月底一共学习了多少天?”全班同学大致呈现了以下两种算法:(1)31-8=23(天)(2)31-8+1=24(天),第一种算法的同学认为,求“经过的天数”就可以用“后一天”去减“前一天”;第二种算法的同学进行了反驳,认为“两头”(指“8日”和“31日”)都要算,所以要加1。在后来的争论中,全班同学达成了共识,同意“两头都算”的观点,但第一种算法的同学仍然不服气,提出了这样一个问题:“两头都算,为什么相减后再加1?”第二种算法的同学也没有说出个所以然,只有几个同学说出了这样的话:“我在奥数班学过,有这样的公式。”后来,笔者翻阅了三年级的《小学数学奥林匹克起跑线》,结果还真是如此。看来,同学们对“31-8+1=24(天)”这个算式本身没有深刻地理解,只是单纯地记忆和模仿。之后,针对此问题,在我校数学教研组内开展了研讨交流,大部分教师同意第二种算法,认为“求经过天数的计算,一般都这样做,这样考填空题时学生就不会做错”,而对其他算法的研究从未涉及,更没有深入地思考。所以,在后来的测试中,很多学生还是会忘记“加1”。
二、问题的现实性追问
追问一,一般都这样做?
显而易见,教师对“经过天数的计算”这一抽象的知识,是根据自身的教学经验,潜意识地把“一般”的模式强加给孩子,认为只要学生循规蹈矩地照做,考试没有太大问题。教师此时关注的焦点只是问题解决的结果,对学生的数学思维并没有关注。而对学生而言,也只是一种“纯记忆”层面上的掌握。教师采取强灌式教学,学生根本不理解其意义,而且也很难让他们理解,其根本原因是教师没有关注学生真实的思考。
追问二,考试不会做错?
很显然,教师教的最终目的只是为了使学生在考试中少出错,让学生死死地记住类似“31-8+1=24(天)”这样的算法,并用它去解决“经过天数的计算”的问题,从而达到应付考试的目的。但是学生在后来的考试中为什么还是会“老忘记加1”呢?因为学生是在被动地接受,缺乏学习过程的真正体验。看来,教师忽视了学生基本活动经验的积累。相反的,如果这一数学结论的建立,是通过有效数学活动的引领,让学生反复验证,在理解中提升,那么学生的记忆也定会更加深刻。因此教师只有基于学生的“学”设计教学过程,学生才会真正理解知识形成的过程,举一反三,灵活运用,从而提升数学思维能力,学校也才能提高教育教学质量。
三、实践的理论性思考
作为一线教师,教学实践会为我们提供很多鲜活真实的案例,诸如上述问题,它会为我们的教学研究提供丰厚的土壤。同时也更加需要我们站在理论的高度剖析案例,这样才会促进研究更加科学和深入。因此教学实践的理论性反思就显得尤为重要。
上面的实例,让我们再一次思考教师的“教”与学生的“学”之间的关系。如何处理好两者的关系,对提升教学质量是至关重要的。但不管选择何种教学方式,一定要基于学生的“学”来展开,从学生的“学”来设计教师的“教”,如果脱离了学生,“教”也就失去了价值。“教”的最终目的是为了让学生学“会”、学“懂”、学“用”。
1.“经过天数的计算”教学中,学生“学”的问题在哪里?
“经过天数的计算”是“年、月、日”单元的练习部分的内容,教材以水稻的生长期为例展开教学,如图1所示。
本题设计的目的一方面是巩固学生对年、月、日单元知识的掌握;另一方面是让学生体会数学与生活的紧密联系。但基于学生的“学”,有很大的难度。具体有以下两个方面:
(1)知识本身体系的复杂。“经过天数的计算”是在学生已经掌握了大月、小月、平年、闰年等知识之后的一个综合运用。这些复杂的知识并不是单独存在的,而是相互联系的若干个知识点的糅合,形成“经过天数的计算”的知识储备。反过来,只有让学生熟练掌握这些知识,才会帮助他们形成解决此问题的技能。
正因为“经过天数的计算”牵扯的知识点较多,而学生大脑的存储容量是有限的,根据他们已有的认知水平,理解与运用知识的能力还略显薄弱,因此,学生在实际运用时会有一定的难度。
(2)学生自身思维的定式。针对低年级学生的年龄特征和思维特点,他们在头脑中已经形成的知识体系往往是被“固化”的,极容易造成思维的定式,而且在一定的时期内也是很难被改变的。在学习本知识之前,学生已经学过有关“周年”和“经过时间”的计算。比如:1949年10月1日-2009年10月1日,经过多少周年?列式为:2009-1949=60;上午8时-下午1时,经过了几小时?算式为:13-8=5。以上两种类型的解题方法都是存储于学生大脑的深刻记忆,根据大脑皮层的记忆功能,遇到类似问题时,他们会条件反射地用“后一个年份(时刻)减前一个年份(时刻)”,因此,学生在解决“经过天数的计算”问题时,也会习惯性地类比迁移,用“后一天去减前一天”来解决问题,从而导致在计算过程中出现错误。
2.如何基于学生的“学”,促进学生对数学知识的理解?
(1)借助“形象直观”,顺应学生的思维点拨。数学是思维的科学,在新的课程标准中,也更加强调关注学生的思维发展。小学阶段,学生的思维大多以“具体形象思维”为主,他们往往会借助图形、图像、图式和形象性的符号来思考,从而使问题更具形象性。因此,借助“形象直观”,可以把复杂的问题简单化,把抽象的问题具体化,让学生轻松地获取知识。在分析学生出现的问题后,借助课堂上的再次实践,进行有效的思维点拨。
【教学片段】
师:小明从7月8日开始学习游泳,到本月底一共学习了多少天?你能想出让同学们能理解的方法吗?
生1:可以用手数,8、9、10、11……
生2:这样太麻烦,可以画图。
师追问:画什么图?
生2:画线段图。
师:你为什么会想到画线段图?
生1:因为画图比较清楚。
生2:画图很容易把题做出来
师:你们能画一画,算一算吗?试试看。
全班同学开始进行独立思考,这时有一位同学用了这样的一种表示方法,如图2所示。
师:你是怎么想到线段图的?
生:因为以前在哪里见过,好像是学习24时计时法的时候。
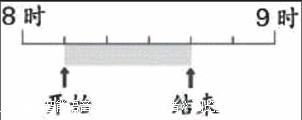
教师这时顺势引导孩子想到了“24时计时法”中的“求经过的时间”,如图3所示。
生2:我比较喜欢用这种方法
……
很显然,学生通过画线段图,清晰地呈现了知识的脉络,便于理解知识间的内在关系。学生们都认为要计算“经过的天数”,就可以用“总天数-不算的天数=经过的天数”,算式为:31-7=24(天),很容易理解与运用,知识的掌握也会更加深刻。
(2)利用“迁移类比”,帮助学生建立数学模型。在新的课程标准中,反复强调了数学的基本思想,其中“模型思想”是比较重要的思想之一。其实数学的本质就是在不断抽象、概括、模式化的过程中发展和丰富起来的。因此,帮助学生建立“经过天数的计算”的数学模型,进行数学问题必要的抽象,才会使学生的数学学习更加深入,才算是一种真正意义上的数学学习。因此我又设计了以下两个层次的教学:
第一层次——巧用迁移,“磨”深数学问题。迁移在心理学上也称学习迁移或训练迁移,是指一种学习对另一种学习的影响。学生对求类似“从7月8日开始学习游泳,到本月底一共学习了多少天?”的问题已经积累了一定的认知经验,因此,可以利用学习迁移,加大数学问题的难度。于是,笔者在原有题目的基础上进行改造:“7月8日开始学习游泳,到8月12日一共学习了多少天?”学生在充分理解的基础上,得出以下方法:先算从7月8日到本月底要经过多少天?31-7=24(天),再算从8月1日到8月12日要经过12天,最后把24天和12天加起来等于36天。看来只要学生理解了问题的发生和发展过程,即使问题变得更难,遇到同类问题时会融会贯通,举一反三。
第二层次——活用类比,“模”化数学模型。对于上述问题,如果我们的教学止步于此,看似学生学会了,其实学得不够彻底,不够深入。数学教学就是要引导帮助学生从已有的知识经验出发,让学生经历将现实问题抽象成数学模型的过程,也就是让学生经历“数学化”的过程,这种教学才是深远而又有价值的。
因此,在学生掌握了具体求“经过天数的计算”的方法后,笔者又把问题进行及时的梳理与总结,利用类比思维帮助学生建立数学模型,让学生在概括中提升,在“建模”中内化。
学生通过独立思考、小组交流后,有以下发现:
(1)“经过天数的计算”如果计算范围是在同一个月的,可以用“总天数-不算的天数=经过的天数”;如果计算范围不是在一个月的,也可以先算到本月月底要经过多少天,再接着算出后面的天数。
(2)有的小组用了这样一个式子来表示:b-a-1,并且还在a-1的下面用“ ”标记,说明先算……
(3)关于这类问题的运用,大部分学生想到了考试、学籍、比赛中的“排序号”问题,比如:15到30;这个考场一共有多少名考生;三(6)班学籍号是从25到66,这个班有多少人;等等
通过以上发现,我们不难看出,教师抓住了知识间的联系,让学生充分展开探索的过程,而并非直接的讲解和告诉,主要训练和培养学生抽象、概括、举一反三的学习能力,再借助“直观线段图”的形象支撑,建立起求“经过天数的计算”的模型。这种模型的建立既加深了学生对知识的理解,又帮助学生实现了数学抽象以及运用抽象模型的能力,为后续学习打下了坚实的基础。
总之,在教学中我们要基于学生的“学”,关注学生“学”中的问题,来合理选择教师的“教”,让“教”与“学”互动交融,缔造出和谐有效的数学课堂。
(作者单位:江苏省徐州市铜山区实验小学)
(责任编辑:陈淑燕)

