基于GA－LM融合的星敏感器参数标定算法

乔 兴，王宏力，王永胜，崔祥祥，陆敬辉

(第二炮兵工程大学303教研室，陕西西安710025)

1 引言

星敏感器是天文导航系统(Celestial Navigation System，CNS)中重要的姿态测量元件，是当前姿态输出精度最高、得以广泛应用的光学姿态敏感器［1］。星敏感器虽为高精度仪器，但星敏感器的多种参数误差极大的影响了姿态矢量的获取精度。因此，为提高星敏感器的测量精度和可靠性，获得高测角精度，必须要对星敏感器参数误差进行标定补偿。

国内外许多学者对星敏感器的参数标定算法已有大量研究，目前，常用的标定算法有最小二乘算法、卡尔曼滤波算法及改进的滤波算法、遗传算法等，以上各种算法都能够满足不同条件的指标要求，但也存在标定精度过低、对标定初始值依赖性强等问题。其中最小二乘算法存在占用存储空间大、计算量过大、对于非线性、多目标问题精度较低，且受到初始值影响较大等问题，滤波算法主要存在计算量大、收敛时间长、精度受复杂环境影响较大，遗传算法主要存在不易精确收敛到全局最优解［2－4］。

基于以上问题本文提出一种基于GA－LM(Genetic Algorith算法与Levenberg－Marquardt算法)融合的星敏感器参数标定算法，充分利用了GA算法的全局搜索以及LM算法的局部寻优能力，解决了最小二乘算法依赖初值、易陷入局部收敛以及GA算法标定效率低、标定结果差的问题，对提高制导精度具有重要意义。

2 系统误差对星点坐标的影响

星敏感器在使用中由于工作环境的改变以及长期工作带来的老化和磨损都会造成系统内部参数变化，从而引入系统误差。在实际测量使用中，星敏感器系统误差的存在会直接导致星敏感器星点坐标的测量误差，对于具体的误差影响因数和数值关系还需要更加具体。因此，要准确描述星点成像的几何关系，主要考虑以下误差因素:1)视轴交点的不准确，也就是视轴的指向发生偏移，记为(x0，y0);2)焦距f的不确定;3)CCD焦平面倾斜，假设焦平面相对理想情况X轴正向转动了x角度、Y绕轴转动了y;4)CCD焦平面绕视轴旋转了β角，记为旋转角β;5)光学镜头的畸变:镜头畸变包括径向和切向畸变，径向畸变会引起图像点沿径向移动，离中心点越远其变形越大;切向畸变引起的误差比较小，可以忽略不计，一般情况下，径向畸变是影响星敏感器标定因素的主要因素［5］，因此只考虑径向畸变。如图1所示。则以上的误差项对星敏感器星像位置坐标影响为［5－7］:

图1 星敏感器误差传递图

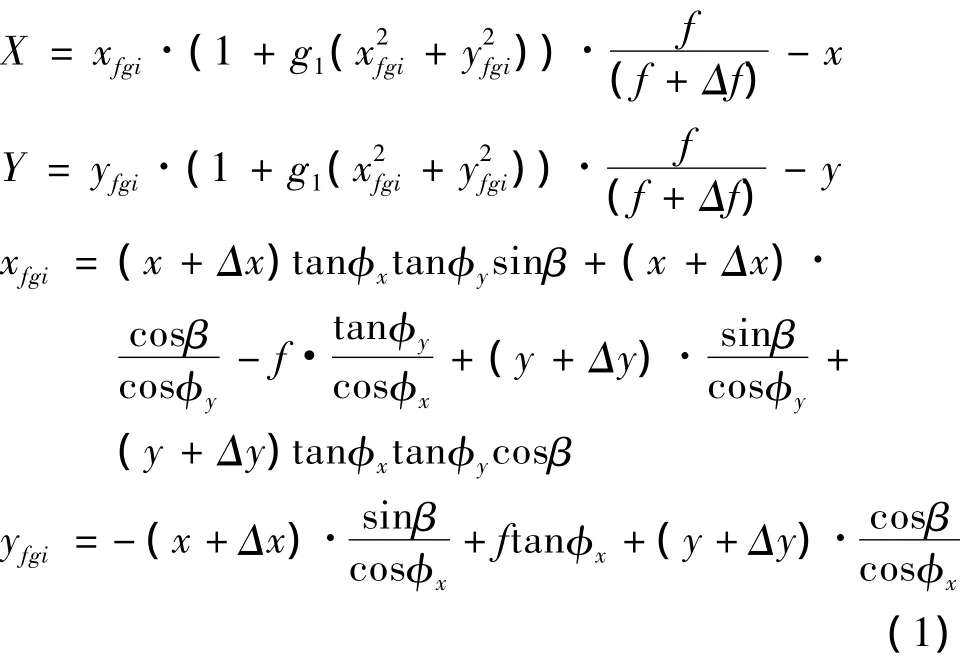
其中，X、Y表示标准星像位置坐标中，星敏器系统误差对星像位置坐标的影响量，即为实测星像坐标与理想成像点的误差校正公式。(x，y)表示标准星像位置坐标;(Δx，Δy)表示主点偏移;x、y、β 分别表示CCD焦平面旋转角以及CCD焦平面绕视轴旋转角。

3 星敏感器参数标定算法设计

3．1 融合标定算法设计

星敏感器标定是一个多参数、大范围、非线性的复杂函数优化问题，在利用最小二乘法进行参数标定时，会有三个缺陷:一是强烈依赖初值;二是容易陷入局部收敛;三是对于非线性、多目标问题精度较低。对于GA算法标定参数，其收敛速度慢，不容易得到最优解，局部搜索能力较弱。

利用改进的最小二乘法——LM算法对参数进行标定，可以扩大收敛范围，使标定过程不易很快陷入局部最优解，但是没有解决强烈依赖初值的问题。

LM算法的迭代公式为:

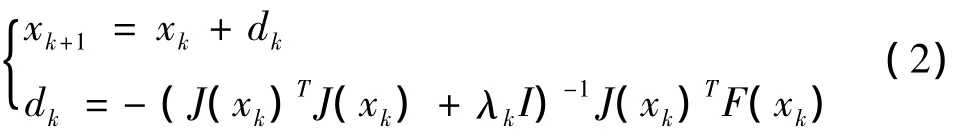
LM算法迭代公式通过引入非负参数λk，克服了满秩要求及坏条件下的迭代缺陷，选择合适的非负参数λk可以确保矩阵J(xk)TJ(xk)+λkI为非奇异。而且能避免出现过大的dk值。此外，当J(xk)奇异时，dk=－(J(xk)TJ(xk))－1J(xk)TF(xk)没有定义，而LM算法是有意义的。而GA算法是以群体搜索特性为最突出特点的一种优化方法，全局搜索能力较强，但标定效率不够高，标定结果不是最优解，只能近似于最优解。

为了充分利用GA算法的全局搜索以及LM算法的局部寻优能力，并解决LM算法依赖初值以及GA算法标定效率低、标定结果差的问题，基于此问题，本文将两种算法进行融合处理，提出一种基于GA－LM融合的星敏感器参数标定算法。

通过理想成像与实际成像坐标的关系可以看出，星敏感器参数存在未修正误差时，将对视场内恒星的成像矢量的计算造成误差，导致工作性能大大降低。所以在使用前必须加以标定校正。对星敏感器参数进行综合标定，最常用的方法是最小二乘法，但其有较多局限性。

3．2 融合算法需要解决的几个问题

(1)GA算法与LM算法的衔接点

本文的融合算法需要解决的问题是GA算法与LM算法的衔接点。本文将通过设定判定准则来解决这一问题，即适应度差值计算法。

连续若干代个体的平均适应度值的差值小于一极小值ε。例如:设目标函数的适应度函数为fitness(x)，第 k代个体适应度的平均值为fitness(xk)，GA算法终止的条件需满足:

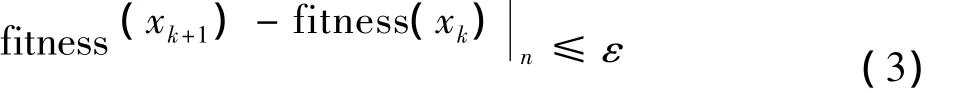
其中，n表示连续n代个体。

第k代的代数确定可以根据收敛过程观察计算法进行确定，即:运用GA算法得到多次优化过程，比较几次收敛图的走势，通过观察收敛过程的方法初步判断趋于稳定或者优化效果不明显的迭代数，如果优化过程各不相同，可以增加优化的次数，或者取几次迭代数的平均值。

(2)适应度函数

本文将根据实验室的相关设备对提出的融合算法进行实验验证。星敏感器参数标定的原理就是要使星敏感器成像模型获得的像点坐标值(x'j，y'j)(j=1，2，…，M)与实际图像的测量值 (xj，yj)(j=1，2，…，M)之间均方根距离的平均值最小。因此，定义适应度函数为:f(θj)=

其中，f(θj)是第j个个体的适应度函数值;(x(θj)，y(θj))为对应于染色体θj和第i幅图像的第j个个体的实际图像测量值;(x'(θj)，y'(θj))为对应于染色体θj和第i幅图像的第j个个体利用星敏感器成像模型获得的像素坐标。

(3)终止条件

在融合算法标定过程中，有两个终止条件需要判定，GA算法的终止条件1利用适应度差值计算法进行计算，连续若干代个体的平均适应度值的差值小于极小正值ε。设目标函数的适应度函数为fitness(x)，第 k代个体适应度的平均值为fitness(xk)，GA算法终止的条件1需满足:

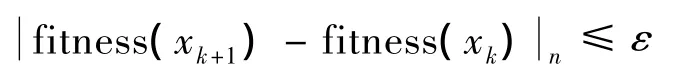
当GA算法达到终止代数后，利用LM算法进行二次寻优，直到达到终止条件2:f(θj)=

即星敏感器成像模型获得的像点坐标值(x'j，y'j)(j=1，2，…，M)与实际图像的测量值 (xj，yj)(j=1，2，…，M)之间均方根距离的平均值最小。

运用GA－LM融合算法进行星敏感器系统参数标定的流程框图如图2所示。

图2 GA－LM融合算法标定星敏感器系统参数的流程图

4 半实物仿真系统的实验验证

为验证融合算法思想的科学性，体现其优越性，将通过半实物系统进行实验验证。

本实验采用的实验室设备包括:多星模拟器硬件、星敏感器模拟器等。

星敏感器模拟器和星模拟器对准，如图3(a)所示是星模拟器中显示的9×7的点阵标准图像，图3(b)是星敏感器中采集的9×7的点阵平面实际成像星图。

图3 标准图像与实际成像

4．1 基于灰度加权法获取星图的质心坐标

灰度值加权法计算质心坐标能充分利用每一点的灰度值信息，而且计算量要比传统的质心计算方法小的多，同时可以满足星图中的精度和实时性要求。本实验中，将运用此方法进行质心的提取。得到标准星图和实际成像中星点的图像坐标值如表1所示。

表1 星点的图像坐标值

4．2 初始参数设置

参数误差根据不同型号的星敏感器实际加工、装配、测量及经验进行设计，具体如下:焦距误差一般应在2%以内，即|Δf|≤0．02f;主点偏移根据经验通常比焦距误差小一个数量级，即一般不会超过10个像素，取|x0|≤0．15mm;根据各种不同型号的星敏感器情况，镜头一阶畸变系数取为:|k1|≤5×10－5;CCD平面的倾斜角α及旋转角β实际中均为比较小的量，取误差最大的情况:|α|≤0．05°，|β|≤0．05°。

用本文方法进行参数标定时，根据提供的设备技术指标，GA算法的初始种群生成范围设置如下:焦距 f=44．8 mm，且 dx=dy=6．5 μm，则［fx，fy］= ［6892，6892］，所以设定 fx，fy∈［6750，7000］;图像的大小为670像素×520像素，所以得到中心图像坐标为(x0，y0)=(335，260)，设定 x0∈［325，345］;y0∈ ［250，270］;径向畸变系数 k1，k2∈［－ 5 × 10－5，5 × 10－5］;倾斜角 αx，αy∈［－ 0．05°，0．05°］;绕光轴 zs轴的旋转角 β ∈ ［－ 0．05°，0．05°］;在该范围内得到初始种群后，利用GA算法开始搜索，GA算法的相关参数设置如表2所示，传统最小二乘算法的初始值设置:归一化焦距［fx，fy］=［6892，6892］，中心图像坐标为(x0，y0)=(335，260)，径向畸变系数k1=k2=0．00005，α =β =0．05°。

4．3 实验结果

采用实验设备对模拟星图利用传统最小二乘算法和GA－LM融合两种算法进行优化，得到优化结果，如表3所示。

表2 GA算法的参数设置

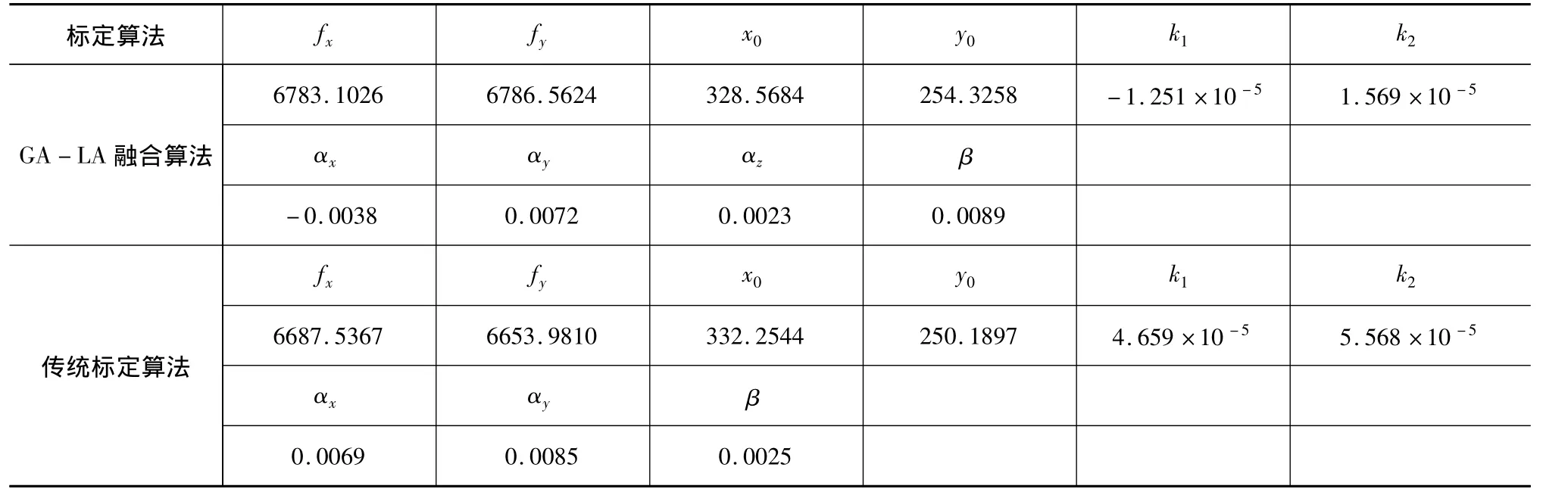
表3 采用模拟星图的标定结果

运用传统最小二乘算法、LM算法、GA算法及融合算法的标定过程如图4所示，

图4 星敏感器参数标定的收敛过程

由图4可知:

(1)最小二乘法标定星敏感器参数受初始参数的取值影响较大，易陷入局部收敛，标定结果稳定性较差;

(2)LM算法改善了最小二乘法易陷入局部收敛以及标定结果不稳定的问题，但强烈依赖初值的问题并没有得到根本解决。

(3)融合算法在140代后利用LM算法二次寻优，局部搜索能力明显加强，标定结果更接近最优解。表明:融合算法充分利用了GA算法的全局搜索以及LM算法局部寻优的能力，GA算法进行大范围搜索为LM算法提供一个合适的初值，解决了LM算法依赖初值以及GA算法标定效率低、标定结果差的问题，与提出融合算法的思路是一致的。

4．4 误差分析

定义图像坐标系的平均误差为星敏感器成像模型投影得到的模拟星点图像坐标(x'i，y'i)(i=1，2，…，m)和模拟星点的实际测量值(xi，yi)(i=1，2，…，m)之间均方根的平均值，以像素为单位，它反映的是求得的星敏感器模型的投影精度。对于N个测试点，其图像坐标的平均绝对误差为:

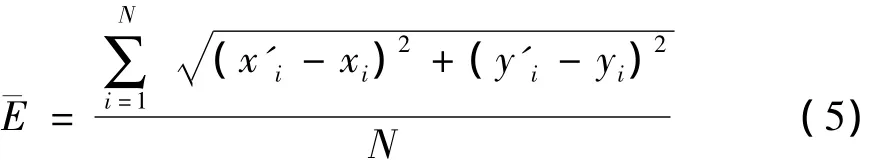
可利用上节中标定的结果计算63个未参与标定测试点的投影误差，如表4所示。

表4 63个未参与标定测试点的投影误差数据

得到63个未参与标定测试点的投影误差如图5所示。

图5 63个测试点的投影误差

综上所述，传统的最小二乘算法相比于优化前的相对误差为0．37207，GA－LM融合算法相比于优化前的相对误差为0．1190。所以得到本文提出的融合算法相比于优化前标定精度提高了88．099%，相比于传统最小二乘法的标定精度提高了68．015%。

5 结论

本文建立了星敏感器的误差模型，并推导了星敏感器误差校正公式;在分析常用参数标定方法的基础上，提出了一种基于GA－LM融合的参数标定算法，通过设计半实物仿真实验，结合实验室相关设备，对融合算法进行了实验验证，结果表明:GALM融合算法相比于优化前的相对误差为0．1190。所以得到本文提出的融合算法相比于优化前标定精度提高了88．099%，相比于传统最小二乘法的标定精度提高了68．015%，对于提高星敏感器的测量精度具有重要应用。

［1］ Mortari D，Junkins，JL．Lost－ in － pace pyramid algorithm for robust star pattern recognition［C］∥24th Annual AAS Guidance and Control Conference，Breckenridge CO，2001，AAS:1 －4．

［2］ Haibo Liu，Xiujian Li，Jichun Tan，et al．Novel approach for laboratory calibration of star tracker［J］．Opt．Engng，2010，49(7):073601．

［3］ LIDe － liang，Ruan Jin．Method adapting to the star sensor’s star extraction［J］．Laser ＆ Infrared，2009，12(39):1348 －1350．(in Chinese)李德良，阮锦．一种适用于星敏感器的星点提取方法［J］．激光与红外，2009，12(39):1348 －1350．

［4］ WANG Cheng，WANG Hongqiang，CHEN Minghua，et al．The analysis and disposal of imaging circuit noise effect on star sensor［J］．Laser ＆ Infrared，2008，38(7):692 －696．(in Chinese)王辰，王宏强，陈明华，等．星敏感器成像电路噪声分析及降噪处理［J］．激光与红外，2008，38(7):692－696．

［5］ WANG Hongtao，LUO Changzhou，WANG Yu，et al．Star sensormodel parametric analysis and calibration method study［J］．J．University of Electronic and Technology of China，2010，39(6):880 －885．(in Chinese)王洪涛，罗长洲，王渝，等．星敏感器模型参数分析及校准方法研究［J］．电子科技大学学报，2010，39(6):880－885．

［6］ PENG Yuan．Study Base on GA camera calibration method［D］．Changsha:National University of Defense Technology，2009．(in Chinese)彭媛．基于遗传算法的摄像机标定方法研究［D］．长沙:国防科学技术大学，2009．

［7］ Carl Christian LIEBE．Accuracy Performance of Star Trackers—A Tutorial［J］．IEEE Trans．On Aerospace and Electronics Systems，2002，38(2):587 －599．